A spring having with a spring constant is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
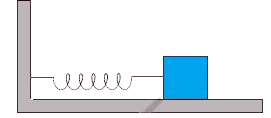
Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.Solution in Gujrati
Since body execute SHM, hence its acceleration,
.
Topper's Solved these Questions
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (ADDITIONAL EXERCISE)
9 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (NUMERICAL FROM DARPAN BASED ON TEXTBOOK)
15 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)
40 Videos
- OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE BOOK - KUMAR PRAKASHANCHAPTER - OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE EXERCISE - CHAPTER - 8 (Match Type questions)
5 Videos
- PHYSICAL WORLDBOOK - KUMAR PRAKASHANCHAPTER - PHYSICAL WORLDEXERCISE - SECTION-E (QUESTIONS FROM MODULE)
9 Videos
Similar Questions
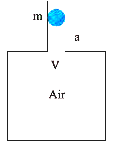
An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
View SolutionThe displacement of a simple harmonic oscillator is given by y=0.40sin(440t+0.61). For this, what are the value of amplitude.
View SolutionOn an average, a human heart is found to beat 75 times in a minute. Calculate its frequency and period.
View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere
View Solution.…. state of substance at very high temperature has generated hope of energy source for mankind.
View SolutionA spring having a spring constant 1200Mn^(-1) is mounted on a horizontal table. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 0.02 m and released. Determine (i) frequency of oscillations (ii) maximum acceleration of the mass and (iii) the maximum speed of the mass.
View SolutionA spring having with a spring constant 1200 N m^(-1) is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released. Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionA spring having with a spring constant 1200 N m^(-1) is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released. Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionA spring having with a spring constant 1200Nm−1 is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.

Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionA spring having with a spring constant 1200Nm−1 is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.

Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionA spring having with a spring constant 1200Nm−1 is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
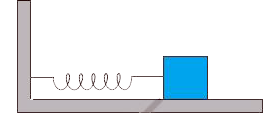
Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionA spring having with a spring constant 1200Nm−1 is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
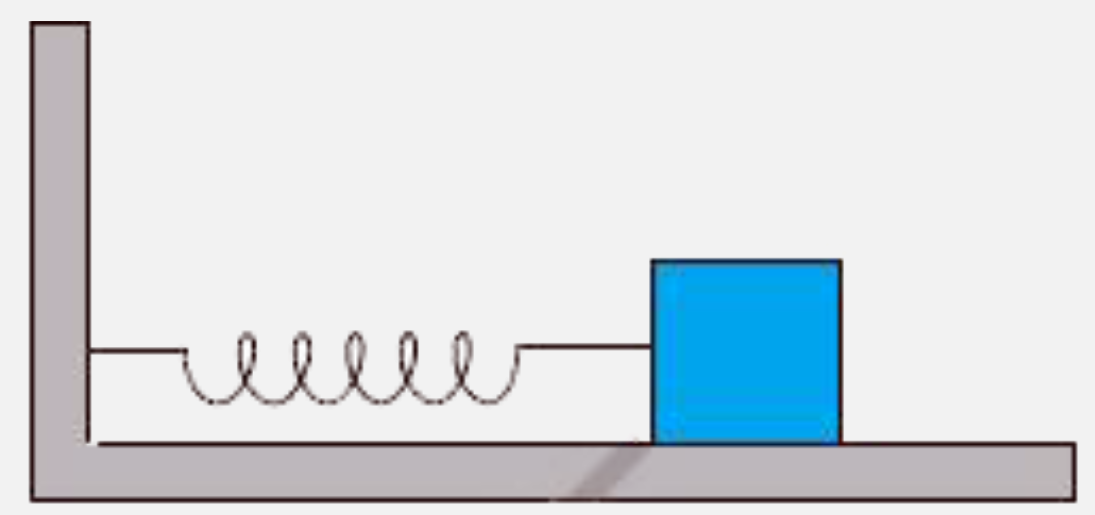
Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionA spring of force constant 1200 Nm−1 is mounted on a horizontal table as shown in Fig.

A mass of 3.0 kg is attached to the free end of the spring, pulled side ways to a distance 2.0 cm and released. Determine the maximum acceleration of the mass.
View SolutionA spring of force constant 1200 Nm−1 is mounted on a horizontal table as shown in Fig.

A mass of 3.0 kg is attached to the free end of the spring, pulled side ways to a distance 2.0 cm and released. Determine the maximum speed of the mass.
View SolutionA spring of force constant 1200Mm−1 Is mounted on a horizontal table as shown in Fig. A mass of 3.0 kg is attached to the free end of the spring, pulled side ways to a distance 2.0 cm and released. Determine

the maximum acceleration of the mass.
View Solution
