A spring is stretched by 0.20 m , when a mass of 0.50 kg is suspended. When a mass of 0.25 kg is suspended, then its period of oscillation will be (g=10m/s2)
0.328 s
0.628 s
0.137 s
1.00 s
The correct Answer is:B
Step by step video, text & image solution for A spring is stretched by 0.20 m , when a mass of 0.50 kg is suspended. When a mass of 0.25 kg is suspended, then its period of oscillation will be (g = 10 m//s^(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A spring is stretched by 5cm by a force 10N. The time period of the oscillations when a mass of 2Kg is suspended by it is
View SolutionThe length of a weigtless spring increaes by 2cm when a weight of 1.0kg in the period of oscillation of the spring and its kinetic energy of oscillation. Take g=10ms−2.
View Solution
Knowledge Check
When a mass of 1 kg is suspended from a spring, it is stretched by 0.4m. A mass of 0.25 kg is suspended from the spring and the spring is allowed to oscillate. If g=10m/s2, then its period of oscillation will be
A0.5 secB0.4 secC0.628 secD1.5 secA spring elongated by length 'L' when a mass 'M' is suspended to it. Now a tiny mass 'm' is attached and then released, its time period of oscillation is -
A2π√(M+m)lMgB2π√mlMgC2π√L/gD2π√Ml(m+M)gWhen a mass M is suspended from a spring, its period of oscillation is 2 second. If a mass 4 M is suspended from the same spring, then its period of oscillation will be
A2 secB1 secC4 secD8 sec
A wire 2 m in length suspended vertically stretches by. 10 mm when mass of 10 kg is attached to the lower end. The elastic potential energy gain by the wire is (take g = 10m/s2)
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
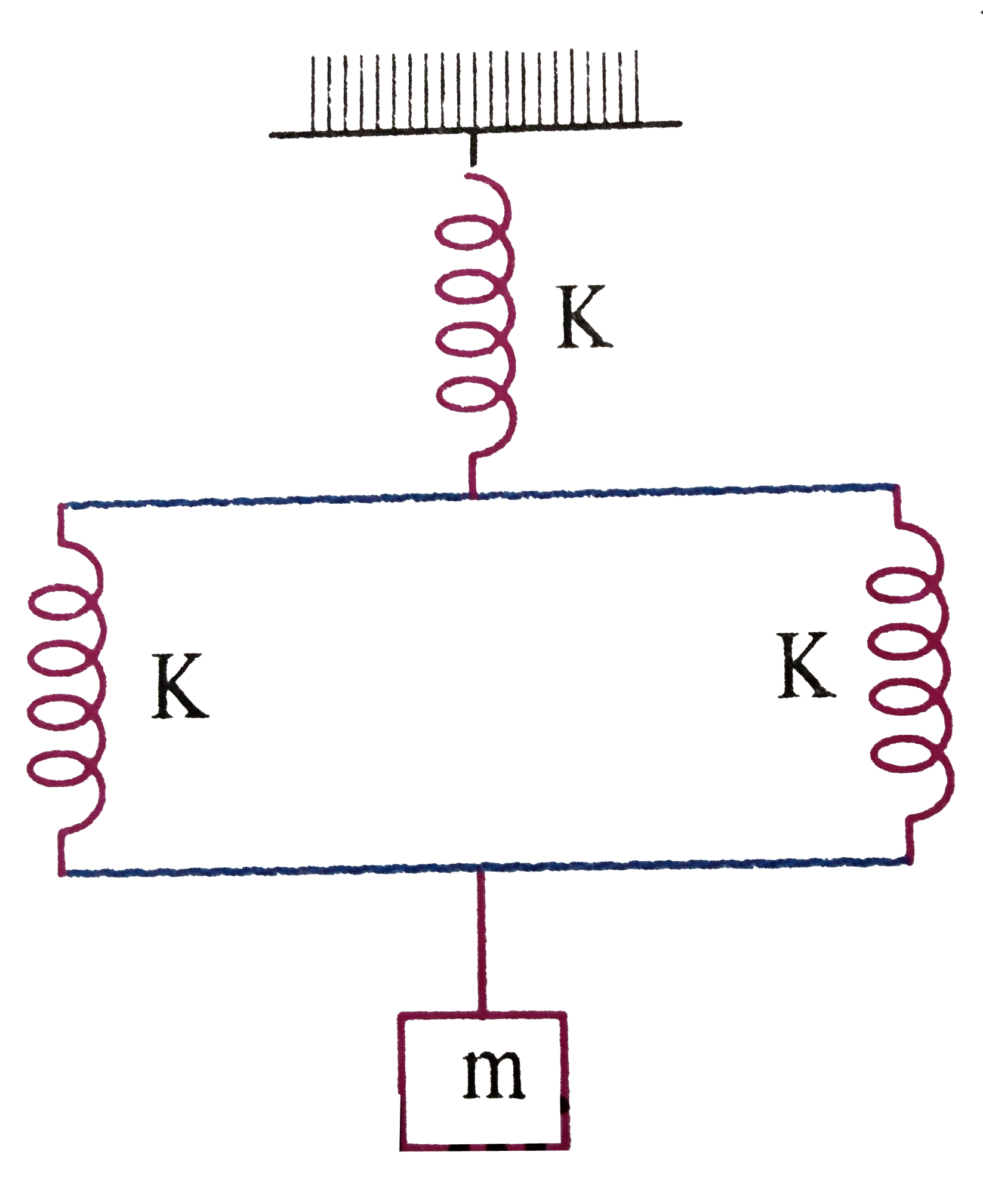
View SolutionIf the period of oscillation of mass M suspended from a spring is one second, then the period of 4M will be
View SolutionIf the period of oscillation of mass m suspended from a spring is 2 s, then the period of mass 4 m will be
View SolutionThe period of oscillation of mass M suspended from a spring of negligible mass is T. If along with it another mass M is also suspended, the period of oscillation will now be
View Solution
