A spring is stretched by applying a load to its free end. The strain produced in the spring is
volumetric
shear
longitudinal and shear
longitudinal
The correct Answer is:C
To find the strain produced in a spring when a load is applied to its free end, we can follow these steps:
Step 1: Understand the Concept of Strain
Strain is defined as the change in length per unit original length. When a load is applied to a spring, it stretches, leading to a change in its length.
Step 2: Identify the Original Length of the Spring
Let the original length of the spring be denoted as L.
Step 3: Determine the Change in Length
When a load is applied to the spring, it stretches by a certain amount, which we can denote as ΔL. This change in length is the result of the applied load.
Step 4: Calculate the Longitudinal Strain
The longitudinal strain (ϵ) can be calculated using the formula:
ϵ=ΔLL
where:
- ΔL is the change in length of the spring,
- L is the original length of the spring.
Step 5: Consider Shear Strain
In addition to longitudinal strain, when a load is applied parallel to the cross-sectional area of the spring, shear strain may also occur. However, for the purpose of this question, we focus primarily on the longitudinal strain.
Step 6: Conclusion
The strain produced in the spring due to the applied load is primarily the longitudinal strain, which can be expressed as:
Strain=ΔLL
Strain is defined as the change in length per unit original length. When a load is applied to a spring, it stretches, leading to a change in its length.
Let the original length of the spring be denoted as L.
When a load is applied to the spring, it stretches by a certain amount, which we can denote as ΔL. This change in length is the result of the applied load.
The longitudinal strain (ϵ) can be calculated using the formula:
ϵ=ΔLL
where:
- ΔL is the change in length of the spring,
- L is the original length of the spring.
In addition to longitudinal strain, when a load is applied parallel to the cross-sectional area of the spring, shear strain may also occur. However, for the purpose of this question, we focus primarily on the longitudinal strain.
The strain produced in the spring due to the applied load is primarily the longitudinal strain, which can be expressed as:
Strain=ΔLL
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LONG SHORT ANSWER TYPE QUESTION
16 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Long Answer Type Questions
3 Videos
- MOTION IN A PLANEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Multiple Choice Questions
37 Videos
Similar Questions
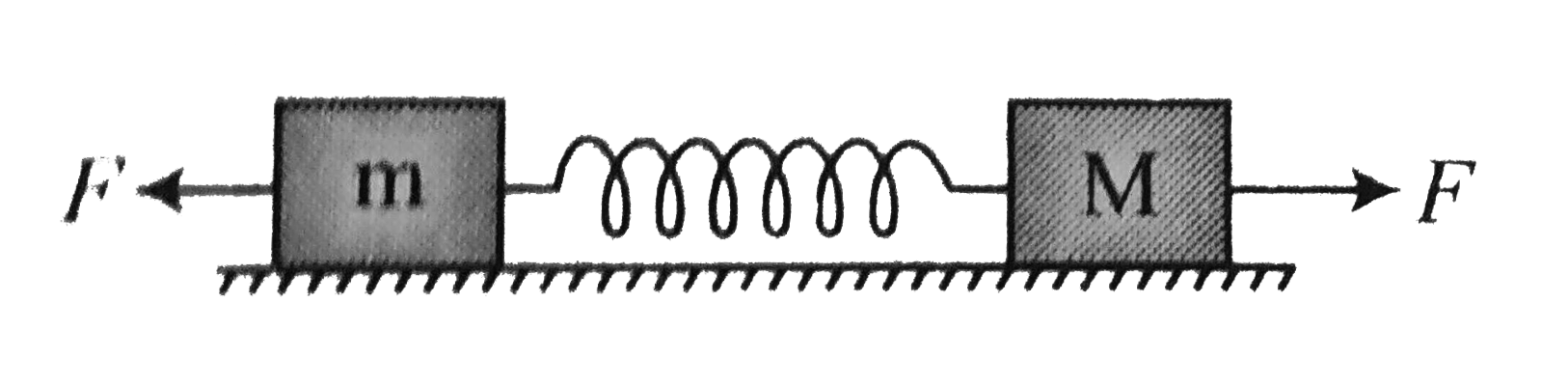
In the situation shown in figure all contact surfaces are smooth. The force constant of the spring is K. Two forces F are applied as shown. The maximum elongation produced in the spring is how many times of F/K (initially the spring is relaxed)?
View SolutionA spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View Solution
Knowledge Check
Natural length of a spring is 60 cm and its spring constant is 4000 N/m. A mass of 20 kg is hung from it. The extension produced in the spring is (Take, g=9.8m/s2)
A4.9 cmB0.49 cmC9.4 cmD0.94 cm
Two springs have their force constants in the ratio of 3:4. Both the springs are stretched by applying equal force F. If elongation in first spring is x then elogation is second spring is
View Solution
A spring having a spring constant k is fixed to a vertical wall as shown in Fig. A block of mass m moves with velocity v torards the spring from a parallel wall opposite to this wall. The mass hits the free end of the spring compressing it and is decelerated by the spring force and comes to rest and then turns the spring is decelerated by the spring force and comes to rest and then turns back till the spring acquires its natural length and contact with the spring is broken. In this process, it regains its angular speed in the opposite direction and makes a perfect elastice collision on the opposite left wall and starts moving with same speed as before towards right. The above processes are repeated and there is periodic oscillation.
Q. What is the time period of oscillation ?
View SolutionA long spring is stretched by 3 cm and its potential energy is V . If the spring is stretched by 6 cm ,its potential energy will be
View SolutionA long elastic spring is stretched by 2cm and its potential energy is U. If the spring is stretched by 10cm, the PE will be
View SolutionA string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160Nm−1 and is stretched by 1.0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring ?
View SolutionA string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160Nm−1 and is stretched by 1.0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring ?
View SolutionA rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.

View Solution