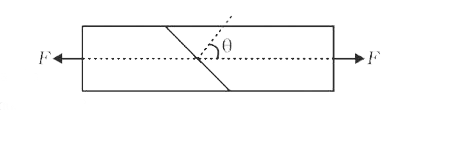
Consider a long steel bar under a tensile stress due to forces F, acting at the edges along the length of the bar

Consider a plane making an angle θ with the length. What are the tensile and shering stresses on this plane ? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?
Consider the adjacent diagram.
Let the cross-sectional area of the bar be A. Consider the equilibrium of the plane aa'. A force F must be acting on this plane making an angle π2−θ with the normal ON. Resolving F into components, along the plane (FP) and normal to the plane.
FP=Fcosθ
FN=Fsinθ
Let the area of the face aa' be A', then
AA'=sinθ
∴ A'=Asinθ
The tensile stress = Normal forceArea=FsinθA'
=FcosθA/sinθ=FAsinθ.cosθ
Shearing stress = Parallel forceArea
=FcosθA/Sinθ=FAsinθ.cosθ
=F2A(2sinθ.cosθ)=F2Asin2θ
(a) For tensile stress to be maximum, sin2θ=1
⇒ sinθ=1
⇒ θ=π2
(b) For shearing stress to be maximum,
sin2θ=1
⇒ 2θ=π2
⇒ θ=π4
Note We must not apply the formula for stress directly, forces must be resolved.

Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LONG SHORT ANSWER TYPE QUESTION16videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Long Answer Type Questions3videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Multiple Choice Questions37videos
MOTION IN A PLANE
Similar Questions
A bar of cross-section A is subjected two equal and opposite tensile forces at its ends consider a plane section of the bar whose makes an angle θ with the axis of the bar.
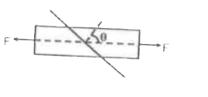
(a) what is the tensile stress on this plane ?
(b)what is the shearing stress on this plane ?
(c )for what value of θ is the tensile stress is maximum ?
(d) for what value of θ is the shearing stress maximum ?View SolutionA long rod of steel under a tensile stress due to the force acting on the edges along the length. The value of angle 0 for which shearing stress is maximum is
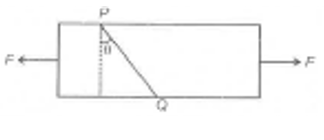 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the question rumber 66, for what value of θ, shearing stress is maximum?
A0∘B30∘C45∘D90∘
A bar of cross section A is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar.

a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of θ is the tensile stress maximum?
d. For what value of θ is the shearing stress maximum?View SolutionA bar of cross-section A is subjected to equal and opposite tensile forces at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar .
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of θ is the tensile stress maximum
(iv) For what value of θ is the shearing stress maximum?
 View Solution
View SolutionBreaking stress depends on
View SolutionDefine stress and strain?
View SolutionHugo de Vries stressed on
View SolutionTensile stress is possible in
View SolutionWhat is thermal stress?
View Solution

