A square loop of wire, edge length a, carries a current i. Compute the magnitude of the magnetic field produced at a point on the axis of the loop at a distance x from the centre.
AP=√x2+a24=√4x2+a22
CP=√AC2+AP2=√x2+a22=√4x2+2a22

sinα=ACAP=a√4x2+2a2
Now B=μ0i4π(AP)2sinα=μ0iaπ√4x2+a2√4x2+2a2
When the fields of all the four sides are considered, the horizontal
components add to zero. So, the total field is given by
BR=4Bcosθ=4μ0ia2π(4x2+a2)√4x2+2a2
For x=0, the expression reduces to BR=4μ0ia2(πa2)√2a2=2√2μ0iπa
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example20videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.135videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK12videos
SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank40videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A square loop of side 6cm carries a current of 30A. Calculate the magnitude of magnetic field B at a point P lying on the axis of the loop and a distance√7 cm from centre of the loop.
View SolutionA square loop of side a=6cm carries a current I=1A. Calculate magnetic induction B(μT) at point P, lying on the axis of loop and at a distance x=√7cm from the centre of loop.
View Solution
Knowledge Check
- Question 1 - Select One
A current - carrying loop is shown in the figure. The magnitude of the magnetic field produced at a point O is
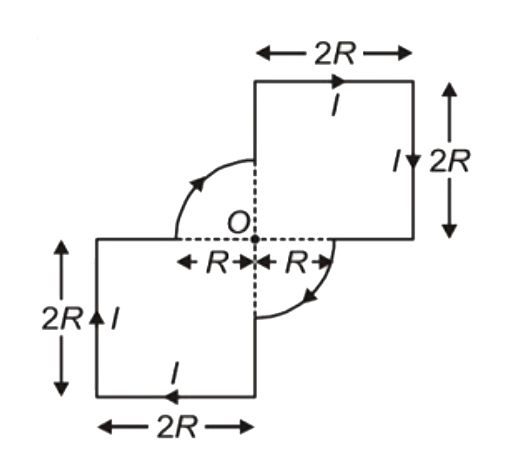 Aμ0I4RBμ0I2R(1+√2π)Cμ0I4R(1+√2π)Dμ04R(1+2√2π)
Aμ0I4RBμ0I2R(1+√2π)Cμ0I4R(1+√2π)Dμ04R(1+2√2π) - Question 2 - Select One
A square loop of edge 'a' carries a current l. The magnetic field at the centre of loop is
Aμ0l2√2πaB2√2μ0lπaCμ0l√2πaDμ0l√2πa - Question 3 - Select One
A square loop of side a carries a current I. The magnetic field at the center of the loop is
A2μ0I√2πaBμ0I√2πaC4μ0I√2πaDμ0Iπa
A circular loop of radius 9.7 cm carries a current 2.3 A. Obtain the magnitude of the magnetic field at the centre of the loop .
View SolutionA circular loop of radius R carries a current I. Obtain an expression for the magnetic field at a point on its axis at a distance x from its centre.
View SolutionTwo circular loops A and B of radii R and 4R are kept concentrically in the same plane. The loops carry currents I1 and I2 respectively. If the magnetic field at a point on the common axis of the loops at a distance 2R from their common centre is zero, the ratio I1I2 is _________.
View SolutionThe magnetic moment of a circular current loop is 2.3×10−5Am2. What is the magnitude of the magnetic field on the axis of the loop at a distance of 1 cm from the loop?
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View Solution

