A circular loop of radius R carries a current I. Obtain an expression for the magnetic field at a point on its axis at a distance x from its centre.

Text Solution

Verified by Experts

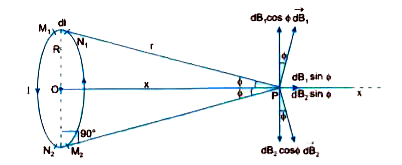
Consider a circular loop of radius R, carrying a current I. Plane of the coil is Y-Z plane (i.e., perpendicular to the plane of paper), while the axis of the loop OX lies in the plane of paper. Consider the circular loop to be divided into large number of current elements $I \to d l$ . Two such elements $N_{1} M_{1} and N_{2} M_{2}$ diametrically opposite to each other, produce the magnetic fields ${- \to d B}_{1}$ and ${- \to d B}_{2}$ perpendicular to both $\to r and \to d l$ and given by right hand rule as,
$∣ ∣ ∣ {- \to d B}_{1} ∣ ∣ ∣ = ∣ ∣ ∣ {- \to d B}_{2} ∣ ∣ ∣ = \frac{μ_{0}}{4 π} \cdot \frac{I d l {sin 90}^{\circ}}{r^{2}} = \frac{μ_{0}}{4 π} \frac{I d l}{(R^{2} + x^{2})}$
These fields may be resolved into components along x-axis and y-axis. Obviously components along y-axis balance each other but components along x-axis are all summed up. Hence, magnetic field due to whole current loop will be:
$B = \oint d B sin ϕ = \oint \frac{μ_{0}}{4 π} \frac{I d l}{(R^{2} + x^{2})} \cdot \frac{R}{\sqrt{(R^{2} + x^{2})}} = \frac{μ_{0} I R}{4 π {(R^{2} + x^{2})}^{3 / 2}} \oint d l$
$= \frac{μ_{0} I R}{4 π {(R^{2} + x^{2})}^{3 / 2}} \cdot 2 π R = \frac{μ_{0} I R^{2}}{2 {(R^{2} + x^{2})}^{3 / 2}}$

Updated on:21/07/2023

A circular coil of radius 2R is carrying current I. The ratio of magnetic fields at the centre of coil and at a point at a distance 6R from centre of coil on axis of coil is
A10
B $10 \sqrt{10}$
C $20 \sqrt{5}$
D $20 \sqrt{10}$
A circular coil of radius R carries a current in it. The magnetic field along its axis decreases as we move away from its centre. The space rate of fall of this field is constant at distance equal to
A2 R
BR
C3 R
DR/2
A circular coil of radius $R$ carries a current $i$ . The magnetic field at its centre is $B$ . The distance from the centre on the axis of the coil where the magnetic field will be $B / 8$ is
A $\sqrt{2} R$
B $\sqrt{3} R$
C $2 R$
D $3 R$