A square plate of mass M and side length L is hinged at one of its vertex (A) and is free to rotate about it. Find the time period of small oscillations if
(a) the plate performs oscillations in the vertical plane of the figure. (Axis is perpendicular to figure.)
(b) the plate performs oscillations about a horizontal axis passing through A lying in the plane of the figure.

2π√2a3g
2π√√2a3g
2π√2√2a3g
2π√2√2ag
The correct Answer is:C
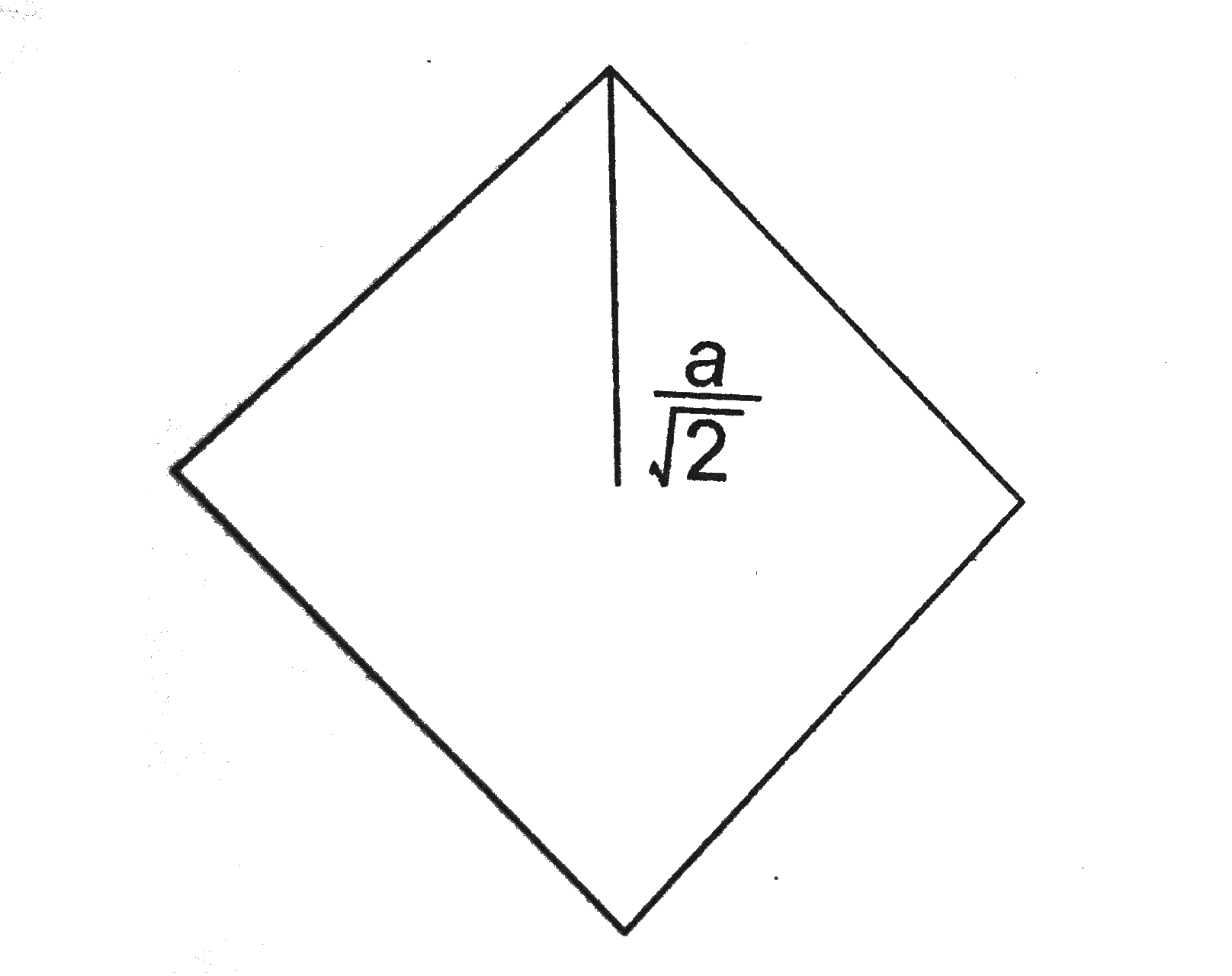
T=2π√1mgd=2π
⎷m(a2+a2)12+m(a√2)2mga√2
=2π√(a6+a2).√2g=2π√2√2a3g
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Problems Based On Mixed Concepts24videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning22videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Simple Pendulum And Different Cases Of Shm25videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
A square plate of mass M and side length L is hinged at one of its vertex (A) and is free to rotate about it. Find the time period of small oscillations if
(a) the plate performs oscillations in the vertical plane of the figure. (Axis is perpendicular to figure.)
(b) the plate performs oscillations about a horizontal axis passing through A lying in the plane of the figure.
 A2π√2a3gB2π√√2a3gC2π√2√2a3gD2π√2√2ag
A2π√2a3gB2π√√2a3gC2π√2√2a3gD2π√2√2ag - Question 2 - Select One
A solid cube of side l is made to oscillate about a horizontal axis passing through one of its edges. Its time period will be
A2π√2√23lgB2π√23lgC2π√√32lgD2π√2√3lg - Question 3 - Select One
A disc is made to oscillate about a horizontal axis passing through mid point of its radius. Determine time period.
A2π√3R2gB2π√2R3gC2π√RgD2π√2Rg
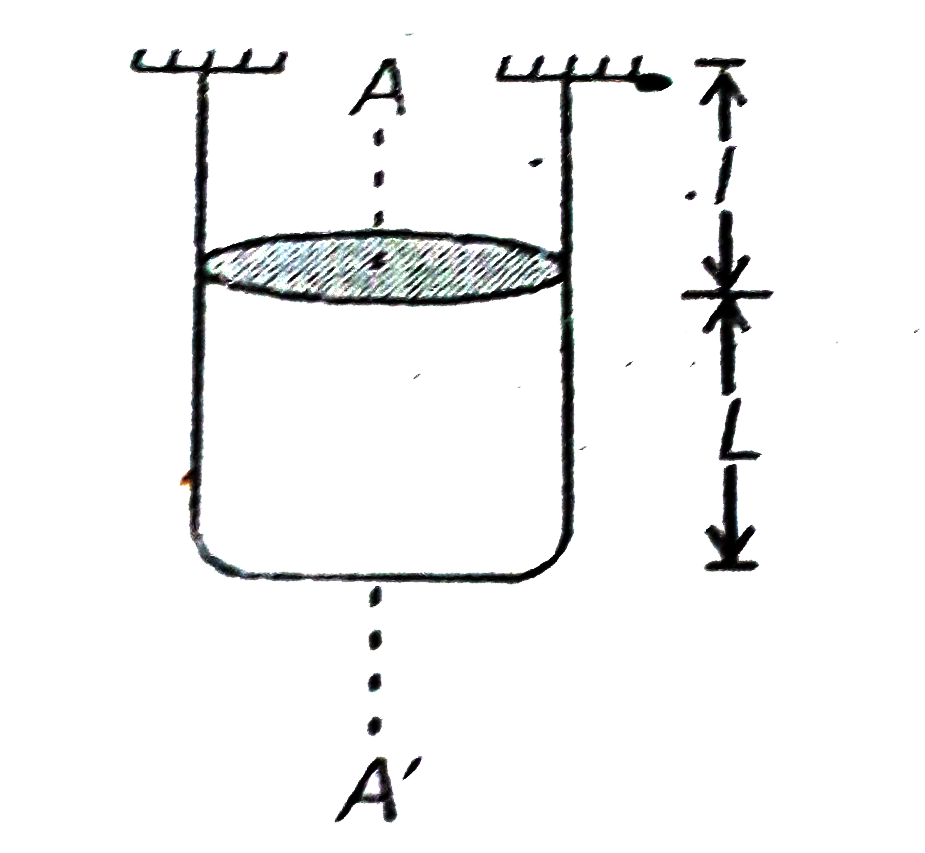
A solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
 View Solution
View SolutionA sphere is made to oscillate about a horizontal tangential axis. Determine time period.
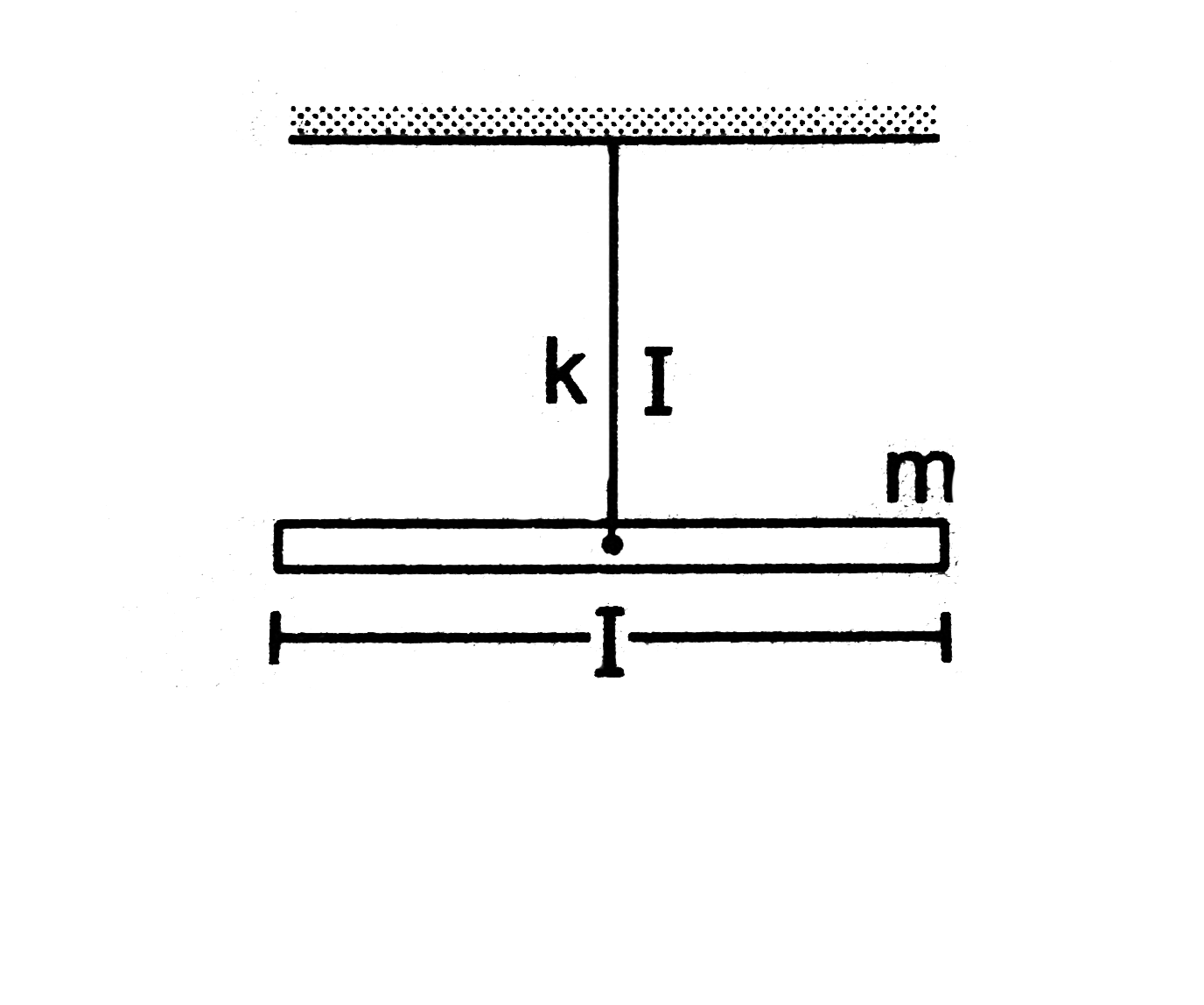
View SolutionA uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time perid iof the system makes a. small oscillations in the vertical plane about the suspension point and b. angular oscillations in the horizontal plane about the centre of the rod.
 View Solution
View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 View Solution
View SolutionA thin uniform rod of length l is pivoted at its upper end. It is free to swing in a vertical plane. Its time period for oscillation of small amplitude is
View Solution

