A square shaped, conducting wire loop of side L, total mass m and total resistance R initially lies in the horizontal x−y plane, with corners at (x,y,z)=(0,0,0),(0,L,0),(L,0,0),and(L,L,0). There is a uniform upward magnetic field in the space within and around the loop. The side of the loop that extends from (0,0,0)→(L,0,0) is held in place on the x-axis, the rest of the loop is released, it begins to rotate due to the gravitational torque.
(a) Find the net torque (magnitude and direction)that acts on the loop when it has rotated through an anglr ϕ from its original orientation and is rotating dounward at an angular speed ω.
(b) Find the angular acceleration of the loop at the instant described in part (a).
( c) Compared to teh case with zero magnetic field, does it take the loop a longer or shorter time to rotate through 90∘ ? Explain.
(d) Is mechanical energy conserved as the loop rotates downward ? Explain.
The correct Answer is:(a) mg(L)2cosϕ−ωB2L4sin2ϕR; (b) 6g5Lcosϕ−12ωB2L25mRsin2ϕ; (c ) Longer, (d) No
(a) magnetic flux passing through the positin when the loop has rotated by an angle ϕ
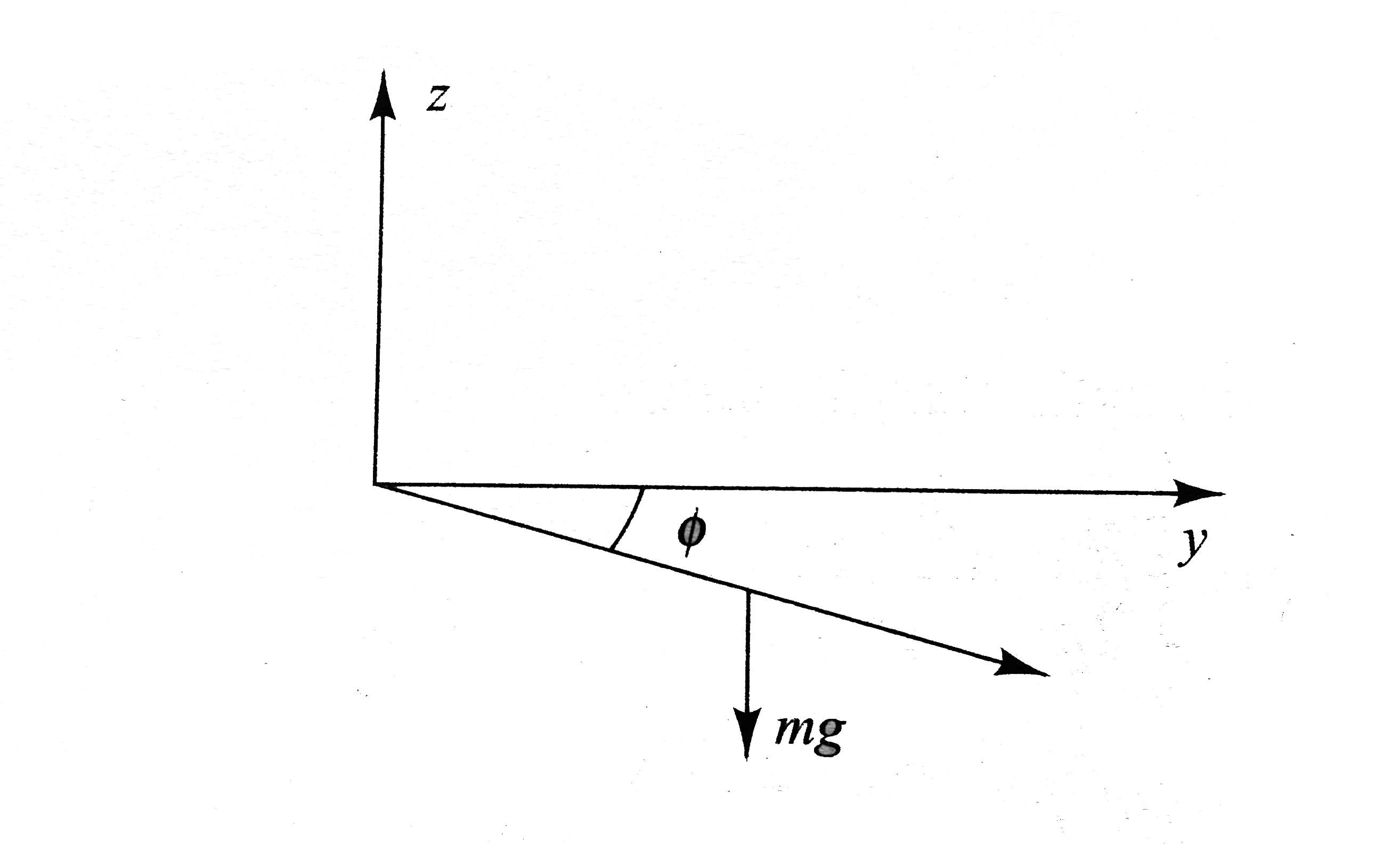
ϕmag=BL2cosθ
|e|=dϕdt=BL2sinϕdϕdt
|e|=BL2(sinϕ)ω
Current through the loop, I=|e|R=BL2(sinϕ)ωR
τmag=MBsinϕ=(IL2)Bsinϕ=B2L4ωsin2ϕR
τgravity=mgL2cosϕ
τnet=mgL2cosϕ−ωB2L4sin2ϕR
(b) τ≠t=Iα, where I=m4L2+2(13m4L2)=512mL2
α=τ≠tI=6g5Lcosϕ−12ωB2L25mRsin2ϕ
( c) Longer, because induced emf opposes the motion of the loop.
(d) No, because some energy will convert into heat due to flow of current.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Single Correct
79 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.2
27 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A loop made of straight edges has six corners at A(0,0,0),B(L,O,0),C(L,L,0),D(0,L,0),E(0,L,L) and F(0,0,L). Where L is in meter. A magnetic field B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionA loop made of straight edegs has six corners at A(0,0,0),B(L,O,0)C(L,L,0),D(0,L,0)E(0,L,L) and F(0,0,L). Where L is in meter. A magnetic field B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionA loop made of straight edegs has six corners at A(0,0,0),B(L,O,0)C(L,L,0),D(0,L,0)E(0,L,L) and F(0,0,L). Where L is in meter. A magnetic field B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionA loop made of straight edegs has six corners at A(0,0,0),B(L,O,0)C(L,L,0),D(0,L,0)E(0,L,L) and F(0,0,L). Where L is in meter. A magnetic field B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is (dependence on L)
View SolutionA square loop EFGH of side a, mass m and total resistance R is falling under gravity in a region of transverse non - uniform magnetic field given by B=By0a =, where B0 is a positive constant and y is the position of side EF of the loop. If at some instant the speed of the loop is v, then the total Lorentz acting on the loop is
View SolutionA square loop of side L, resistance R placed in a uniform magnetic field B acting normally to the plane of the loop. If we attempt to pull it out of the field with a constant velocity v, then the power needed is
View SolutionThe plane lx+my=0 is rotated through an angle α about its line of intersection with the plane z=0 . Prove that the equation of the plane in its new position is lx+my±(√l2+m2tanα)z=0.
View SolutionA triangular loop of side l carries a current l. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View Solution
