Question

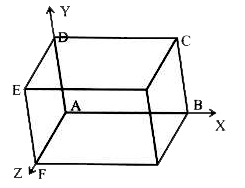
A loop made of straight edegs has six corners at ${\displaystyle A(0,0,0),B(L,O,0)C(L,L,0),D(0,L,0)E(0,L,L)}$ and ${\displaystyle F(0,0,L)}$. Where ${\displaystyle L}$ is in meter. A magnetic field ${\displaystyle B=B_0(\hat{i}+\hat{k})T}$ is present in the region. The flux passing through the loop ${\displaystyle ABCDEFA}$ (in that order) is

Answer

200

Explanation

To find the magnetic flux passing through the loop $$ABCDEFA$$ in the given magnetic field, we can follow these steps:

Step 1: Identify the Points
The corners of the loop are given as:
- \( A(0, 0, 0) \)
- \( B(L, 0, 0) \)
- \( C(L, L, 0) \)
- \( D(0, L, 0) \)
- \( E(0, L, L) \)
- \( F(0, 0, L) \)

Step 2: Determine the Magnetic Field
The magnetic field is given by:
\( \mathbf{B} = B_0 (\hat{i} + \hat{k}) \, \text{T} \)

Step 3: Identify the Planes of the Loop
The loop consists of two main planes:
1. The base plane \( ABCD \) lies in the \( xy \)-plane (where \( z = 0 \)).
2. The vertical plane \( ADEF \) lies along the \( xz \)-plane.

Step 4: Calculate the Area Vectors
- For the base plane \( ABCD \):
- The area vector \( \mathbf{A}_{ABCD} \) is perpendicular to the plane and directed along the \( z \)-axis:
\( \mathbf{A}_{ABCD} = L^2 \hat{k} \)

- For the vertical plane \( ADEF \):
- The area vector \( \mathbf{A}_{ADEF} \) is perpendicular to the plane and directed along the \( x \)-axis:
\( \mathbf{A}_{ADEF} = L^2 \hat{i} \)

Step 5: Combine the Area Vectors
The total area vector \( \mathbf{A} \) for the loop can be expressed as:
\( \mathbf{A} = \mathbf{A}_{ABCD} + \mathbf{A}_{ADEF} = L^2 \hat{k} + L^2 \hat{i} \)

Step 6: Calculate the Magnetic Flux
The magnetic flux \( \Phi \) through the loop is given by the dot product of the magnetic field \( \mathbf{B} \) and the area vector \( \mathbf{A} \):
\( \Phi = \mathbf{B} \cdot \mathbf{A} \)
Substituting the values:
\( \Phi = B_0 (\hat{i} + \hat{k}) \cdot (L^2 \hat{i} + L^2 \hat{k}) \)

Step 7: Compute the Dot Product
Calculating the dot product:
\( \Phi = B_0 \left( L^2 (\hat{i} \cdot \hat{i}) + L^2 (\hat{k} \cdot \hat{k}) \right) = B_0 \left( L^2 (1) + L^2 (1) \right) = B_0 (2L^2) \)

Step 8: Final Result
Thus, the magnetic flux passing through the loop \( ABCDEFA \) is:
\( \Phi = 2B_0 L^2 \, \text{Weber} \)