Question

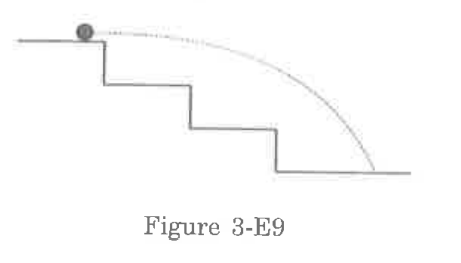
A stair case contains ten steps each 10cm high and 20 cm wide. The minimum horizontal velocity with which the ball has to be rolled off the upper most step, so as to hit directly the edge of the lowest steps is (approximately)

Options

A. `42 ms^(-1)`
B. `4.2 ms^(-1)`
C. `24 ms^(-1)`
D. `2.4 ms^(-1)`

Answer

B

Explanation

To solve the problem of finding the minimum horizontal velocity with which a ball must be rolled off the uppermost step of a staircase to hit the edge of the lowest step, we can follow these steps:

Step 1: Understand the Geometry of the Problem
- The staircase has 10 steps, each 10 cm high and 20 cm wide.
- The total height (h) from the top step to the bottom step is 10 steps × 10 cm/step = 100 cm = 1 m.
- The horizontal distance (range, R) from the edge of the uppermost step to the edge of the lowest step is 20 cm × 9 = 180 cm = 1.8 m.

Step 2: Set Up the Projectile Motion Equations
- The ball will be projected horizontally from the top step, so the initial vertical velocity (Vy) is 0.
- The time (t) it takes to fall from the height (h) can be calculated using the formula for free fall:
\( h = \frac{1}{2} g t^2 \)
where g is the acceleration due to gravity (approximately 9.8 m/s²).

Step 3: Calculate the Time of Flight
- Rearranging the formula gives:
\( t^2 = \frac{2h}{g} \)
Substituting h = 1 m:
\( t^2 = \frac{2 \times 1}{9.8} \approx 0.204 \quad \Rightarrow \quad t \approx \sqrt{0.204} \approx 0.451 \text{ seconds} \)

Step 4: Calculate the Minimum Horizontal Velocity
- The horizontal distance (R) that the ball must travel is 1.8 m.
- The horizontal velocity (u) can be calculated using the formula:
\( R = u \cdot t \)
Rearranging gives:
\( u = \frac{R}{t} \)
Substituting R = 1.8 m and t = 0.451 s:
\( u = \frac{1.8}{0.451} \approx 3.99 \text{ m/s} \)

Conclusion
The minimum horizontal velocity with which the ball has to be rolled off the uppermost step so as to hit directly the edge of the lowest step is approximately 4.0 m/s.