A standing wave is maintained in a homogeneous string of cross - sectional area a and density p . It is formed at y\he superpositions given of two waves travelling in opposite directions given by the equations
3πspω2a22k
πspω2a22k
5πspω2a22k
2πspω2a22k
The correct Answer is:C
To solve the problem of finding the equation of the standing wave formed by the superposition of two waves traveling in opposite directions on a homogeneous string, we will follow these steps:
1. Understanding the Standing Wave:
A standing wave is formed by the interference of two waves traveling in opposite directions. The general form of these waves can be written as:
y1=Asin(kx−ωt)(wave traveling in the positive x-direction)
y2=Asin(kx+ωt)(wave traveling in the negative x-direction)
2. Superposition of the Waves:
The resultant wave y is obtained by adding the two waves:
y=y1+y2=Asin(kx−ωt)+Asin(kx+ωt)
3. Using the Trigonometric Identity:
We can use the trigonometric identity for the sum of sine functions:
sinA+sinB=2sin(A+B2)cos(A−B2)
Applying this to our equation:
y=2Asin(kx)cos(ωt)
4. Identifying the Parameters:
- The amplitude of the standing wave is 2A.
- The wave number k is related to the wavelength λ by k=2πλ.
- The angular frequency ω is related to the frequency f by ω=2πf.
5. Finding the Distance Between Antinodes:
The distance between two consecutive antinodes is given by:
Distance=λ2=πk
6. Calculating the Volume of the String:
The volume V of the string between adjacent antinodes can be expressed as:
V=Distance×Cross-sectional area=πk⋅A
7. Energy Density Calculation:
The energy density u of the string is given by:
u=12ρA2ω2
where ρ is the density of the string.
8. Total Energy Calculation:
The total energy E in the volume V can be calculated as:
E=V⋅(u1+u2)=V⋅(u+u)=V⋅2u
Substituting the expressions for V and u:
E=(πkA)⋅2(12ρA2ω2)=πAρA2ω2k
9. Final Expression for Energy:
Thus, the final expression for the energy E can be simplified to:
E=πAρA2ω2k
Final Answer:
The energy E of the standing wave is given by:
E=5πsρω2A22k
A standing wave is formed by the interference of two waves traveling in opposite directions. The general form of these waves can be written as:
y1=Asin(kx−ωt)(wave traveling in the positive x-direction)
y2=Asin(kx+ωt)(wave traveling in the negative x-direction)
The resultant wave y is obtained by adding the two waves:
y=y1+y2=Asin(kx−ωt)+Asin(kx+ωt)
We can use the trigonometric identity for the sum of sine functions:
sinA+sinB=2sin(A+B2)cos(A−B2)
Applying this to our equation:
y=2Asin(kx)cos(ωt)
- The amplitude of the standing wave is 2A.
- The wave number k is related to the wavelength λ by k=2πλ.
- The angular frequency ω is related to the frequency f by ω=2πf.
The distance between two consecutive antinodes is given by:
Distance=λ2=πk
The volume V of the string between adjacent antinodes can be expressed as:
V=Distance×Cross-sectional area=πk⋅A
The energy density u of the string is given by:
u=12ρA2ω2
where ρ is the density of the string.
The total energy E in the volume V can be calculated as:
E=V⋅(u1+u2)=V⋅(u+u)=V⋅2u
Substituting the expressions for V and u:
E=(πkA)⋅2(12ρA2ω2)=πAρA2ω2k
Thus, the final expression for the energy E can be simplified to:
E=πAρA2ω2k
The energy E of the standing wave is given by:
E=5πsρω2A22k
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - More Than One Option is Correct
23 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Comprehion Type Questions
20 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE MAINS
50 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
A standing wave is maintained in a homogeneous string of cross-sectional area s and density ρ . It is formed by the superposition of two waves travelling in opposite directions given by the equation y1=asin(ωt−kx) and y2=2asin(omegt+kx). The total mechanical energy confined between the sections corresponding to the adjacent antinodes is
View SolutionA standing wave ξ=asinkx.Cosωt is maintained in a homogeneous rod with cross − sectional area S and density ρ. Find the total mechanical energy confined between the sections corresponding to the adjacent displacement nodes.
View SolutionAssertion: Stationary waves are so called because particles are at rest in stationary waves.
Reason: They are formed by the superposition of two identical waves travelling in opposite directions.
View SolutionThe transvers displacement of a string (clamped at its both ends) is given by
y(x,t)=0.06sin(2π3s)cos(120πt)
Where x and y are in m and t in s. The length of the string 1.5m and its mass is 3.0×10−2kg.
Answer the following :
(a) Does the funcation represent a travelling wave or a stational wave ?
(b) Interpret the wave as a superposition of two waves travelling in opposite directions. What is the wavelength. Frequency and speed of each wave ?
Datermine the tension in the string.
View SolutionThe transverse displacement of a string (clamped at its two ends ) is given by
y(x,t)=0.06sin(2π3)xcos(120πt)
wherer x ,y are in m and t ini s. The length of the string is 1.5m and its mass is 3×10−2 kg. Answer the following: (i) Does the function represent a travelling or a stationary wave ?
(ii) Interpret the wave as a superimposition of two waves travelling in opposite directions. What are the wavelength, frequency and speed of propagation of each wave ?
(iii) Determing the tension in the string.
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Figure 7.104( c) shows the standing wave pattern at t=0 due to superposition of waves given by y1 and y2 in Figs.7.104(a) and (b) . In Fig. 7.104 (c ) , N is a node and A and antinode . At this instant say t=0 , instantaneous velocity of points on the string named as A
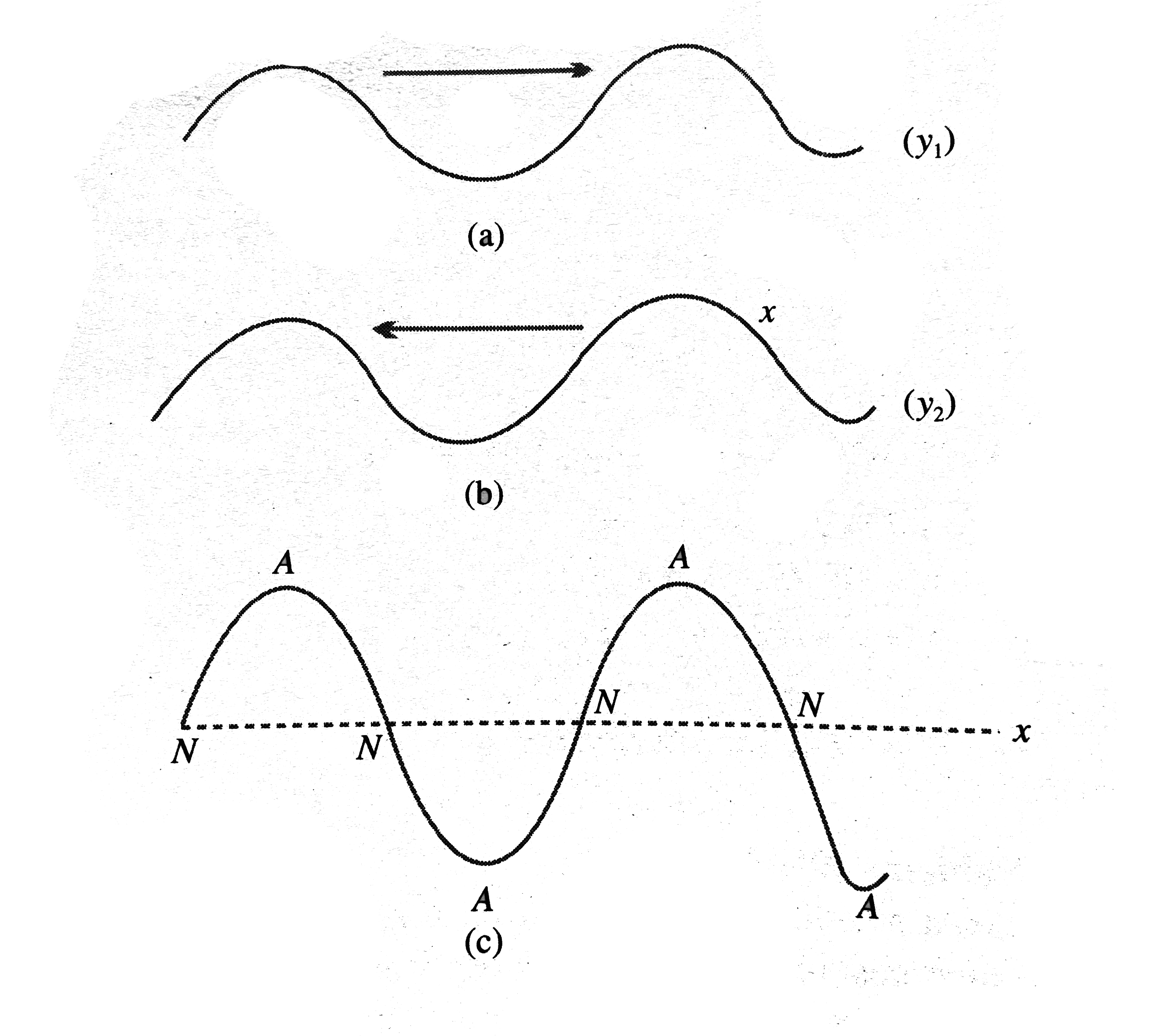
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
If one end of the string is at x=0 , positions of the nodes can be described as
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Amplitude of simple harmonic motion of a point on the string that is located at x=1.8cm will be
View SolutionA travelling wave of amplitude 5A is partically reflected from a bounday with the amplitude 3A. Due to superposition of two waves with different amplitude in opposite direction a standing wave pattern is formed. Datermine the ratio of amplitude at antinode to node.
View Solutiony1=8sin(ωt−kx)andy2=6sin(ωt+kx) are two waves travelling in a string of area of cross-section s and density rho. These two waves are superimposed to produce a standing wave.
(a) Find the energy of the standing wave between two consecutive nodes.
(b) Find the total amount of energy crossing through a node per second.
View Solution
