A standing wave ξ=asinkx.Cosωt is maintained in a homogeneous rod with cross − sectional area S and density ρ. Find the total mechanical energy confined between the sections corresponding to the adjacent displacement nodes.
The correct Answer is:A, B, D
To find the total mechanical energy confined between the sections corresponding to adjacent displacement nodes of a standing wave in a homogeneous rod, we can follow these steps:
Step 1: Identify the Length Between Nodes
The standing wave is given by the equation:
ξ=Asin(kx)cos(ωt)
The distance between adjacent displacement nodes is half the wavelength, which can be expressed as:
L=λ2
Step 2: Determine the Kinetic Energy
The kinetic energy dT of an element of length dx in the rod can be expressed as:
dT=12mv2=12ρSdx(∂ξ∂t)2
Calculating the time derivative of ξ:
∂ξ∂t=−Aωsin(kx)sin(ωt)
Thus,
(∂ξ∂t)2=A2ω2sin2(kx)sin2(ωt)
Substituting this back into the expression for kinetic energy:
dT=12ρSdx⋅A2ω2sin2(kx)sin2(ωt)
Step 3: Integrate Kinetic Energy Over One Node Length
To find the total kinetic energy T between two nodes, integrate dT from 0 to λ2:
T=∫λ2012ρSA2ω2sin2(kx)sin2(ωt)dx
Using k=2πλ, we can rewrite the integral:
T=12ρSA2ω2sin2(ωt)∫λ20sin2(kx)dx
The integral ∫λ20sin2(kx)dx evaluates to λ4:
T=12ρSA2ω2sin2(ωt)⋅λ4
Step 4: Determine the Potential Energy
The potential energy dU can be expressed as:
dU=12ρS(∂ξ∂x)2dx
Calculating the spatial derivative:
∂ξ∂x=Akcos(kx)cos(ωt)
Thus,
(∂ξ∂x)2=A2k2cos2(kx)cos2(ωt)
Substituting this into the expression for potential energy:
dU=12ρSdx⋅A2k2cos2(kx)cos2(ωt)
Step 5: Integrate Potential Energy Over One Node Length
To find the total potential energy U between two nodes, integrate dU:
U=∫λ2012ρSA2k2cos2(kx)cos2(ωt)dx
The integral ∫λ20cos2(kx)dx also evaluates to λ4:
U=12ρSA2k2cos2(ωt)⋅λ4
Step 6: Total Mechanical Energy
The total mechanical energy E is the sum of kinetic and potential energy:
E=T+U
Substituting the expressions for T and U:
E=(12ρSA2ω2sin2(ωt)⋅λ4)+(12ρSA2k2cos2(ωt)⋅λ4)
Final Expression
Using k=2πλ and simplifying, we can express the total mechanical energy confined between the sections corresponding to the adjacent displacement nodes.
The standing wave is given by the equation:
ξ=Asin(kx)cos(ωt)
The distance between adjacent displacement nodes is half the wavelength, which can be expressed as:
L=λ2
The kinetic energy dT of an element of length dx in the rod can be expressed as:
dT=12mv2=12ρSdx(∂ξ∂t)2
Calculating the time derivative of ξ:
∂ξ∂t=−Aωsin(kx)sin(ωt)
Thus,
(∂ξ∂t)2=A2ω2sin2(kx)sin2(ωt)
Substituting this back into the expression for kinetic energy:
dT=12ρSdx⋅A2ω2sin2(kx)sin2(ωt)
To find the total kinetic energy T between two nodes, integrate dT from 0 to λ2:
T=∫λ2012ρSA2ω2sin2(kx)sin2(ωt)dx
Using k=2πλ, we can rewrite the integral:
T=12ρSA2ω2sin2(ωt)∫λ20sin2(kx)dx
The integral ∫λ20sin2(kx)dx evaluates to λ4:
T=12ρSA2ω2sin2(ωt)⋅λ4
The potential energy dU can be expressed as:
dU=12ρS(∂ξ∂x)2dx
Calculating the spatial derivative:
∂ξ∂x=Akcos(kx)cos(ωt)
Thus,
(∂ξ∂x)2=A2k2cos2(kx)cos2(ωt)
Substituting this into the expression for potential energy:
dU=12ρSdx⋅A2k2cos2(kx)cos2(ωt)
To find the total potential energy U between two nodes, integrate dU:
U=∫λ2012ρSA2k2cos2(kx)cos2(ωt)dx
The integral ∫λ20cos2(kx)dx also evaluates to λ4:
U=12ρSA2k2cos2(ωt)⋅λ4
The total mechanical energy E is the sum of kinetic and potential energy:
E=T+U
Substituting the expressions for T and U:
E=(12ρSA2ω2sin2(ωt)⋅λ4)+(12ρSA2k2cos2(ωt)⋅λ4)
Using k=2πλ and simplifying, we can express the total mechanical energy confined between the sections corresponding to the adjacent displacement nodes.
Topper's Solved these Questions
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Comprehension Based
3 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary
30 Videos
Similar Questions
A standing wave is maintained in a homogeneous string of cross-sectional area s and density ρ . It is formed by the superposition of two waves travelling in opposite directions given by the equation y1=asin(ωt−kx) and y2=2asin(omegt+kx). The total mechanical energy confined between the sections corresponding to the adjacent antinodes is
View SolutionA standing wave is maintained in a homogeneous string of cross - sectional area a and density p . It is formed at y\he superpositions given of two waves travelling in opposite directions given by the equations
View Solution
Knowledge Check
A long straight cable of length l is placed symmetrically along z-axis and has radius a(<<l). The cable consists of a thin wire and a co- axial conducting tube. An alternating current I(t)=I0 sin (2πvt). Flows down the central thin wire and returns along the co-axial conducting tube. the induced electric at a distance s from the wire inside the cable is
E(s,t)=μ0I0v cos (2πvt)In(sa)ˆk.
(i) Calculate the displacement current density inside the cable.
(ii) Integrate the displacement current density across the cross- section of the cable to find the total displacement current Id.
(iii) compare the conduction current I0 with the displacement current Id0.A2πλ2I0ln(as)sin(2πυt)ˆkB1λ2I0ln(as)sin(2πυt)ˆkCπλ2I0ln(as)sin(2πυt)ˆkDZero
A longitudinal standing wave y=acoskxcosωt is maintained in a homogeneious medium of density ρ. Here ω is the angular speed and k , the wave number and a is the amplitude of the standing wave . This standing wave exists all over a given region of space.
If a graph E(=Ep+Ek) versus t , i.e., total space energy density verus time were drawn at the instants of time t=0 and t=T/4, between two successive nodes separated by distance λ/2 which of the following graphs correctly shows the total energy (E) distribution at the two instants.
View SolutionA longitudinal standing wave y=acoskxcosωt is maintained in a homogeneious medium of density ρ. Here ω is the angular speed and k , the wave number and a is the amplitude of the standing wave . This standing wave exists all over a given region of space.
The space density of the potential energy PE=Ep(x,t) at a point (x,t) in this space is
View SolutionA longitudinal standing wave y=acoskxcosωt is maintained in a homogeneious medium of density ρ. Here ω is the angular speed and k , the wave number and a is the amplitude of the standing wave . This standing wave exists all over a given region of space.
The space density of the kinetic energy . KE=Ek(x,t) at the point (x,t) is given by
View SolutionA standing wave is formed by two harmonic waves, y1=Asin(kx−ωt)andy2=Asin(kx+ωt) travelling on a string in opposite directions. Mass density is 'ρ' and area of cross section is S. Find the total mechanical energy between two adjacent nodes on the string.
View Solutiony1=8sin(ωt−kx)andy2=6sin(ωt+kx) are two waves travelling in a string of area of cross-section s and density rho. These two waves are superimposed to produce a standing wave.
(a) Find the energy of the standing wave between two consecutive nodes.
(b) Find the total amount of energy crossing through a node per second.
View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H ).Find the speed of the vessel with which it move
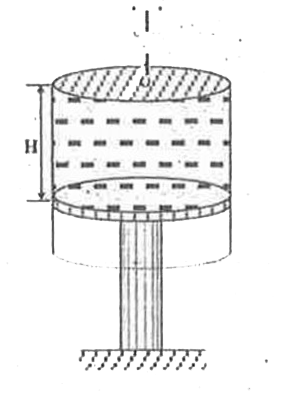
View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H )
Speed of the liquid with which it comes out of the vessel is

View Solution
