A standing wave y=2Asinkxcosωt is set up in the wire AB fixed at both ends by two vertical walls (see Fig. 3.197). The region between the walls contains a constant magnetic field B. Now answer the following question:

The wire is found to vibrate in the third harmonic. The maximum emf induced is
(a) 4(AB)ωk
(b) 3(AB)ωk
( c) 2(AB)ωk
(d) ABωk
The correct Answer is:A
(a) y=2Asinkxcosωt
v=dydt=−2Asinkxωsinωt
vmax=−2Aωsinkx,k=3πAB
e=∫l=AB0bvmaxdx=−2aωB∫AB0sinkxdx=+2ωABk[cos(3π)ABAB−cosθ]=−4(AB)ωk
ωt=π2
t=π2ω
For second harmonic k=2πAB
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Integer
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Archives Fill In The Blanks
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A standing wave y=2Asinkxcosωt is setup in the wire AB fixed at both ends by two vertical walls (see the figure). the region between the wall contains a constant magnetic field B. Now answer the following questions.
In the above question, the time when the emf becomes maximum for the first time is
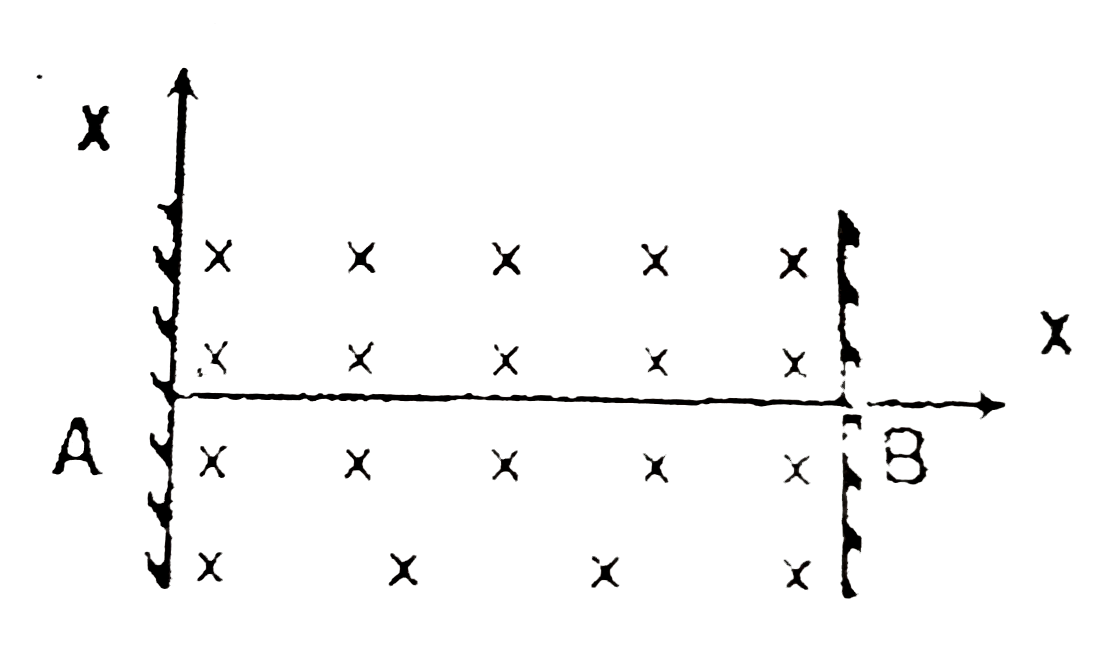
View Solution(i) The equation of wave in a string fixed at both end is y=2sinπtcosπx. Find the phase difference between oscillations of two points located at x=0.4m and x=0.6m.
(ii) A string having length L is under tension with both the ends free to move. Standing wave is set in the string and the shape of the string at time t=0 is as shown in the figure. Both ends are at extreme. The string is back in the same shape after regular intervals of time equal to T and the maximum displacement of the free ends at any instant is A. Write the equation of the standing wave.

View Solution
Knowledge Check
A stsnding wave y=2Asinkxcosωt is set up in the wire AB fixed at both ends by two vertical walls (see Fig. 3.197). The region between the walls contains a constant magnetic field B. Now answer the following question:

In the above qestion, the time when the emf becomes maximum for the time isA(a) 2πωB(b) πωC( c) π2ωD(d) π4ωA stsnding wave y=2Asinkxcosωt is set up in the wire AB fixed at both ends by two vertical walls (see Fig. 3.197). The region between the walls contains a constant magnetic field B. Now answer the following question:

In which of the following modes the emf induced in AB is always zero?A(a) fundamental modesB(b) second harmonicC( c) ssecond overtoneD(d) fourth overtoneThere are two infinite parallel current carrying wires in vertical plane. Lower wire is fixed and upper wire is having a linear mass density λ. Two wires are carrying currents I1 and I2. Now upper wire is placed in a magnetic field produced by lower wire. Magnetic field due to lower wire at the location of upper wire is μ0I2πd, where I1 current lower wire, d separation between wires.
Force on any small portion of upper wire having length dl is dF=μ0I1I2dl2πd, where I2 current in the upper wire. If directions of current in the wires is appropriate then upper wire can be in equilibrium if its weight is balanced by magnetic force. Now answer the following questions.
If upper wire is slightly displaced from its mean position and released it will perform simple harmonic motion. As wire then total mechanical energy of wireARemains constantBDecreasesCWe can't say anything about mechanical energy in magnetic fieldDIncreases
An aluminimum wire of cross - sectional area 1×10−6m2 is joined to a steel wire of the same cross - sectional area . This compound wire is stretched on a sonometer , pulled by a weight of 10kg. The total length of the compound wire between the bridges is 1.5m of which the aluminium wire is 0.6m and the rest is steel wire . Transverse vibrations are set up in the wire by using an external source of variable frequency . Find the lowest frequency of excitation for which standing waves are formed , such that the joint in the wire is a node . What is the total number of nodes observed at this frequency , excluding the two at the ends of the wire ? The density of aluminium is 2.6×103kg/m3 and that of steel is 1.04×104kg/m3
View SolutionThe four wire loops shpwn figure have vertical edge lengths of either L,2L or 3L. They will move with the same speed into a region of uniform magnetic field →B directed out of the oage. Rank them according to the maximum magnitude of the induced emf greatest to least.

View SolutionEstimation of frequency of a wave forming a standing wave represented by y=Asinkxcost can be done if the speed and wavelength are known using speed=Frequency×wavelength . Speed of motion depends on the medium properties namely tension in string and mass per unit length of string . A string may vibrate with different frequencies . The corresponding wavelength should be related to the length of the string by a whole number for a string fixed at both ends . Answer the following questions:
A string fixed at both ends having a third overtone frequency of 200Hz while carrying a wave at a speed of 30ms−1 has a length of
View SolutionEstimation of frequency of a wave forming a standing wave represented by y=Asinkxcost can be done if the speed and wavelength are known using speed=Frequency×wavelength . Speed of motion depends on the medium properties namely tension in string and mass per unit length of string . A string may vibrate with different frequencies . The corresponding wavelength should be related to the length of the string by a whole number for a string fixed at both ends . Answer the following questions:
Speed of a wave in a string forming a stationary wave does not depend on
View SolutionEstimation of frequency of a wave forming a standing wave represented by y=Asinkxcost can be done if the speed and wavelength are known using speed=Frequency×wavelength . Speed of motion depends on the medium properties namely tension in string and mass per unit length of string . A string may vibrate with different frequencies . The corresponding wavelength should be related to the length of the string by a whole number for a string fixed at both ends . Answer the following questions:
If y=10sin5xcos2tm represents a stationary wave then , the possible one of the travelling waves causing this is
View Solution
