A star like the sun has serveral bodies moving around it at different distance. Consider that all of them are moving in circular orbits. Let $r$ be the distance of the body from the centre of the star and let its linear velocity be $υ$ , angular velocity $ω$ , kinetic energy $K$ , gravitational potential energy $U$ , total energy $E$ and angular momentum $L$ . As the radius $r$ of the orbit increase, determine which of the above quantities increase and which ones decrease.

Video Solution

Text Solution

Verified by Experts

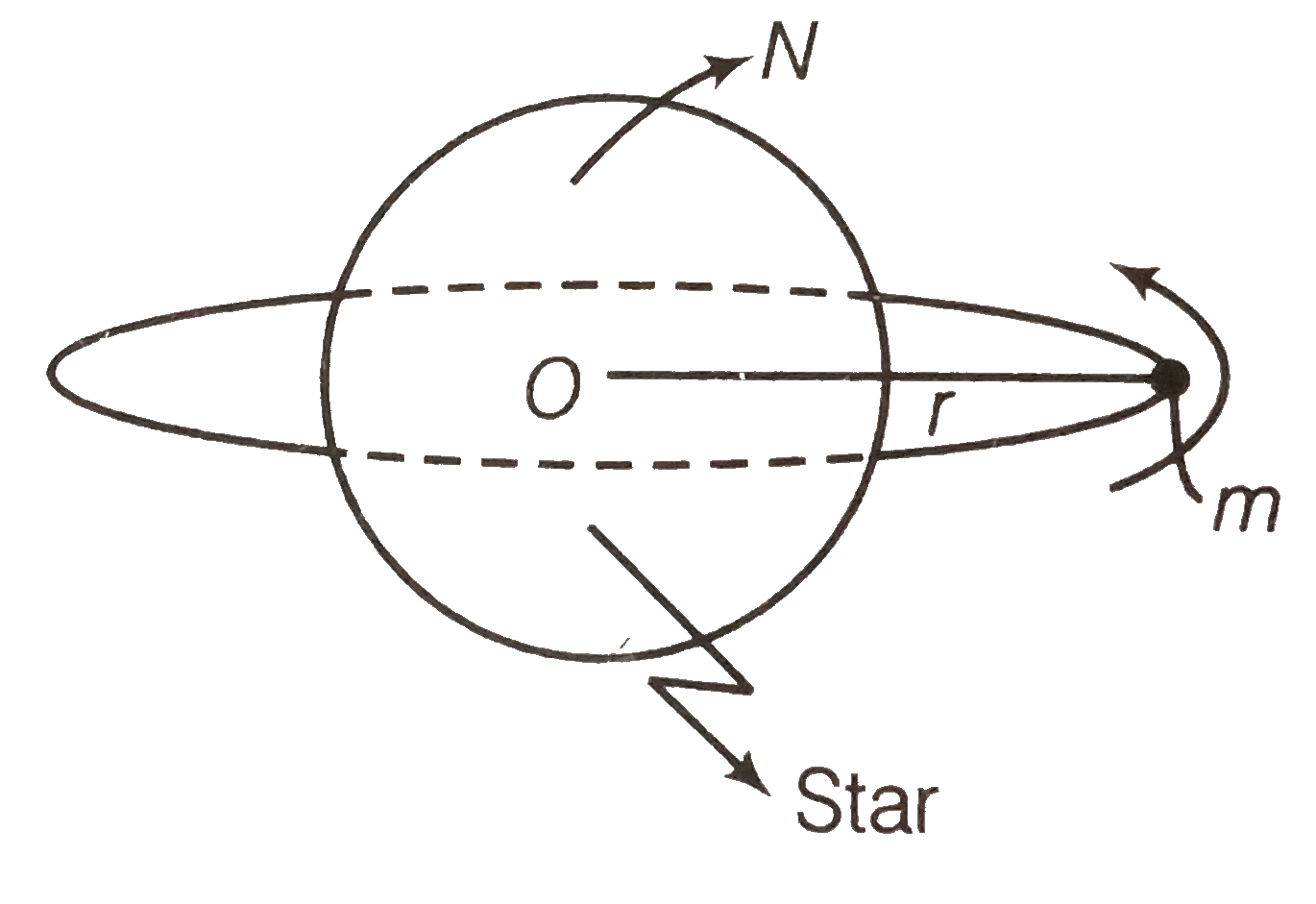
The situation is shown in the diagram, where a body of mass $m$ is revolving around a star of mass M.
Linear velocity of the body $v = \sqrt{\frac{G M}{r}}$
$\Rightarrow v \propto \frac{1}{\sqrt{r}}$
Therefore, when r increases, v decreases
Angular velocity of the body $ω = \frac{2 π}{T}$
According to Kepler's law of period,
$T^{2} \propto r^{3} \Rightarrow T = k r^{3 / 2} (∴ ω = \frac{2 π}{T})$
Therefore, when r increases, $ω$ decreases.
Kinetic energy of the body $K = \frac{1}{2} m v^{2} = \frac{1}{2} m \times \frac{G M}{r} = \frac{G M m}{2 r}$
$∴ K \propto \frac{1}{r}$
Therefore, when r increases, KE decreases
Gravitational potential energy of the body,
$U = - \frac{G M m}{r} \Rightarrow U \propto - \frac{1}{r}$
Therefore, when r increases, PE becomes less negative i.e., increases.
Total energy of the body $E = K E + P E = \frac{G M m}{2 r} + (- \frac{G M m}{r}) = - \frac{G M m}{2 r}$
Therefore, when r increases, total energy becomes less negative, i.e., increases.
Angular momentum of the body $L = m v r = m r \sqrt{\frac{G M}{r}} = m \sqrt{G M r}$
$∴ L \propto \sqrt{r}$
Therefore when r increases, angular momentum L increases.
Note In this case, we have not considered the sun -object system as isolated and the force on the system is not zero. So, angular momentum is not conserved.

Updated on:21/07/2023