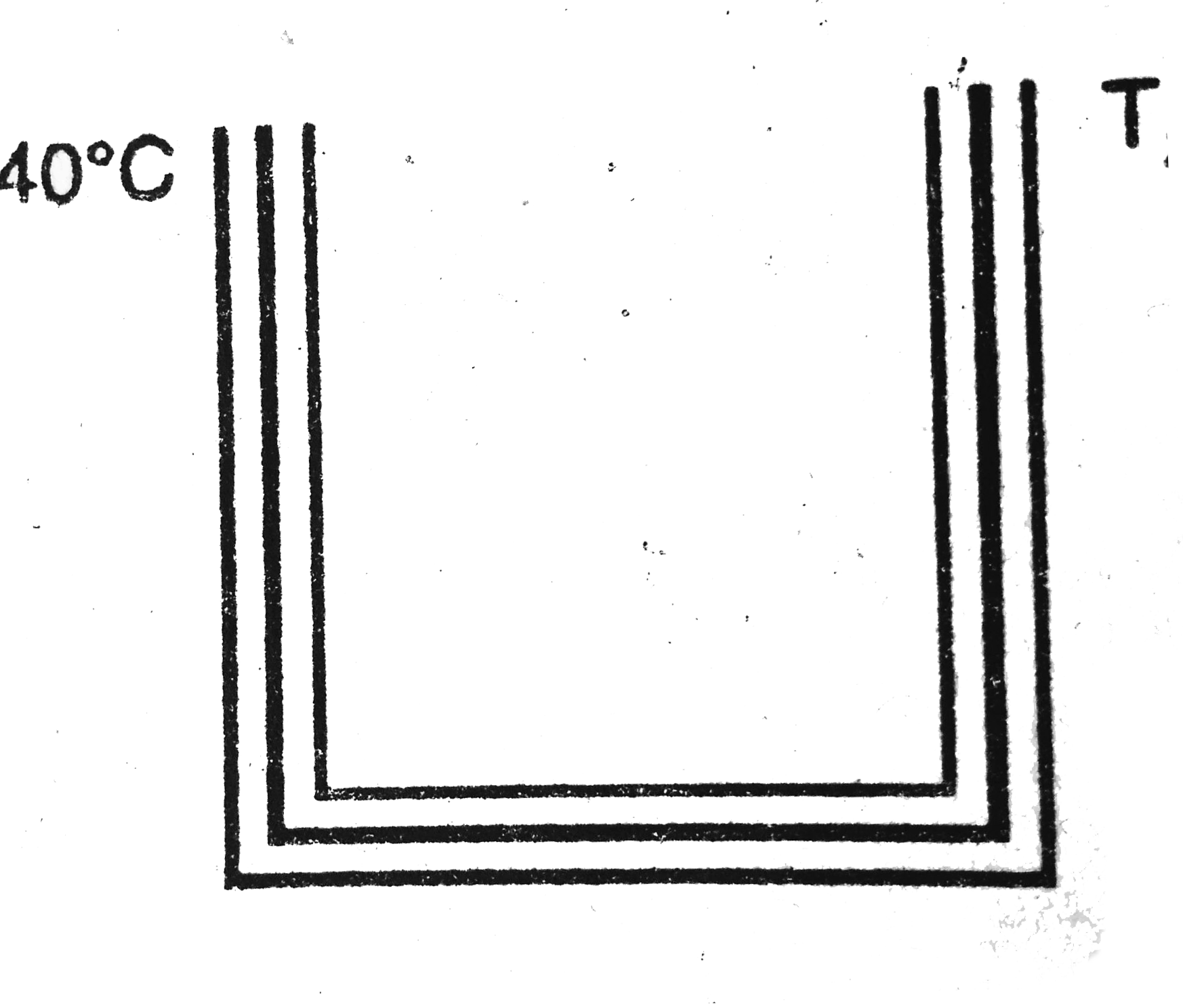
A steel farme (K=45Wm^(-1)^(@)C^(-1) of total length 60cm and cross se

Three conducting rods of same material and cross-section are shown in figure. Temperatures of A,D and C are maintained at $20^{\circ} C, 90^{\circ} C and 0^{\circ} C$ . The ratio of lengths BD and BC if there is no heat flow in AB is

A $\frac{2}{7}$
B $\frac{7}{2}$
C $\frac{9}{2}$
D $\frac{2}{9}$
The ends of copper rod of length $1 m$ and area of cross section $1 c m^{2}$ are maintained at $0^{\circ} C$ and $100^{\circ} C$ . At the centre of rod, there is a source of heat of $32 W$ . The thermal conductivity of copper is $400 W / m K$
AThe temperature of rod at centre is $250^{\circ} C$
BThe temperature of rod at centre is $50^{\circ} C$
CThe temperature gradient in right half is $500^{\circ} C / m$
DThe temperature gradient in left half is $300^{\circ} C / m$
$0.5$ mole of an ideal gas at constant temperature $27^{\circ} C$ kept inside a cylinder of length $L$ and cross-section area A closed by a massless piston The cylinder is attached with a conducting rod of length $L$ cross-section area $(1 / 9) m^{2}$ and thermal conductivity k whise other end is maintained at $0^{\circ} C$ If piston is moved such that rate of heat flow through the conducing rod is constant then find velocity of piston when it is at height $L / 2$ from the bottom of cylinder [Neglect any kind of heat loss from system
.
A $\frac{k}{50 R}$
B $\frac{k}{100 R}$
C $\frac{k}{110 R}$
D $\frac{k}{90 R}$

A steel farme $(K = 45 W m^{- 1}$ ^(@)C^(-1) $o f \to t a l \leq n > h$ 60cm $and c r o s s sec t i o n a r e a$ 0.02cm^(2) $, F or m s t h r e e s o f a □ . T h e e e e n d s a r e m a \int a \in e d a t$ 20^(@)C $and$ 40^(@)C . Find the rate of heat flow through a cross section of the frame.