A steel wire and a copper wire of equal length and equal cross- sectional area are joined end to end and the combination is subjected to a tension. Find the ratio of
copper/steel
(a) the stresses developed . In the two wires,
(b) the strains developed. (Y of steel )
The correct Answer is:A, B, C
To solve the problem, we need to find the ratio of stresses and strains developed in a steel wire and a copper wire that are joined end to end and subjected to the same tension.
Given Data:
- Young's modulus of steel (Y_steel) = 2×1011N/m2
- Young's modulus of copper (Y_copper) = 1.3×1011N/m2
- Both wires have equal length (L) and equal cross-sectional area (A).
1. Understanding Stress:
Stress (σ) is defined as the force (F) applied per unit area (A):
σ=FA
2. Applying Tension:
Since both wires are subjected to the same tension (T) and have the same cross-sectional area (A), the stress in both wires will be the same:
σsteel=TAandσcopper=TA
3. Calculating the Ratio of Stresses:
σcopperσsteel=T/AT/A=1
Therefore, the ratio of stresses developed in copper to steel is:
Ratio of stresses=1:1
(b) Finding the Ratio of Strains Developed
1. Understanding Strain:
Strain (ε) is defined as the change in length (ΔL) divided by the original length (L):
ϵ=ΔLL
2. Using Young's Modulus:
Young's modulus (Y) relates stress and strain:
Y=σϵ
Rearranging gives:
ϵ=σY
3. Calculating Strains for Both Wires:
For steel:
ϵsteel=σsteelYsteel=T/AYsteel
For copper:
ϵcopper=σcopperYcopper=T/AYcopper
4. Calculating the Ratio of Strains:
ϵcopperϵsteel=T/AYcopper÷T/AYsteel=YsteelYcopper
Substituting the values:
ϵcopperϵsteel=2×10111.3×1011=21.3=2013
5. Final Ratio of Strains:
Therefore, the ratio of strains developed in copper to steel is:
Ratio of strains=20:13
Final Answers:
- (a) The ratio of stresses developed: 1:1
- (b) The ratio of strains developed: 20:13
- Young's modulus of steel (Y_steel) = 2×1011N/m2
- Young's modulus of copper (Y_copper) = 1.3×1011N/m2
- Both wires have equal length (L) and equal cross-sectional area (A).
Stress (σ) is defined as the force (F) applied per unit area (A):
σ=FA
Since both wires are subjected to the same tension (T) and have the same cross-sectional area (A), the stress in both wires will be the same:
σsteel=TAandσcopper=TA
σcopperσsteel=T/AT/A=1
Therefore, the ratio of stresses developed in copper to steel is:
Ratio of stresses=1:1
Strain (ε) is defined as the change in length (ΔL) divided by the original length (L):
ϵ=ΔLL
Young's modulus (Y) relates stress and strain:
Y=σϵ
Rearranging gives:
ϵ=σY
For steel:
ϵsteel=σsteelYsteel=T/AYsteel
For copper:
ϵcopper=σcopperYcopper=T/AYcopper
ϵcopperϵsteel=T/AYcopper÷T/AYsteel=YsteelYcopper
Substituting the values:
ϵcopperϵsteel=2×10111.3×1011=21.3=2013
Therefore, the ratio of strains developed in copper to steel is:
Ratio of strains=20:13
- (a) The ratio of stresses developed: 1:1
- (b) The ratio of strains developed: 20:13
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 2 Single Correct
10 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 2 More Than One Correct
8 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 1 Single Correct
16 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
469 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
A steel wire and a copper wire of equal length and equal cross sectional area are joined end to end and the combination is subjected to a tension. Find the ratio of a. The stresses developed in the two wire and b. the strains developed. Y of steel =2×1011Nm−2. Y of copper =1.3×1011Nm−2.
View SolutionTwo wires of equal cross section but one made of steel and the other of copper, are joined end to end. When the combination is kept under tension, the elongations in the two wires are found to be equal. Find the ratio of the lengths of the two wires. Young modulus of steel =2.0×1011Nm−2 and that of copper =1.1×1011Nm−2
View SolutionA steel wire and copper wire of the same diameter and of length 1m and 2m respectively are connected end to end and a force is applied. The increase in length of the combination is 0.01m.Calculate the elongation produced in the individual wires. Given that Y of copper is 12×1010Nm2 and that of steel is 20×1010Nm−2.
View SolutionA steel wire and a copper wire, identical in all respects are to be stretched equally. On which wire more work has to be done.
View SolutionIn figure the upper wire is made of steel and the lower of copper. The wires have equal cross section. Find the ratio of the longitudinal strains developed in the two wires.

View SolutionA brass of length 2m and cross-sectional area 2.0cm2 is attached end to end to a steel rod of length and cross-sectional area 1.0cm2. The compound rod is subjected to equal and oppsite pulls of magnitude 5×104N at its ends. If the elongations of the two rods are equal, the length of the steel rod (L) is
{YBrass=1.0×1011N/m2 and Ysteel=2.0×1011N/m2
View SolutionA steel wire of original length 1m and cross-sectional area 4.00mm2 is clamped at the two ends so that it lies horizontally and without tension. If a load of 2.16kg is suspended from the middle point of the wire, what would be its vertical depression ?
Y of the steel =2.0×1011Nm−2. Take g=10ms−2
View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390Wm−1C−1 and that of steel =46Wm−1C−1 .

View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390WM−1.∘C−1 and that of steel =46Wm−1.∘C−1 .

View SolutionA rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2
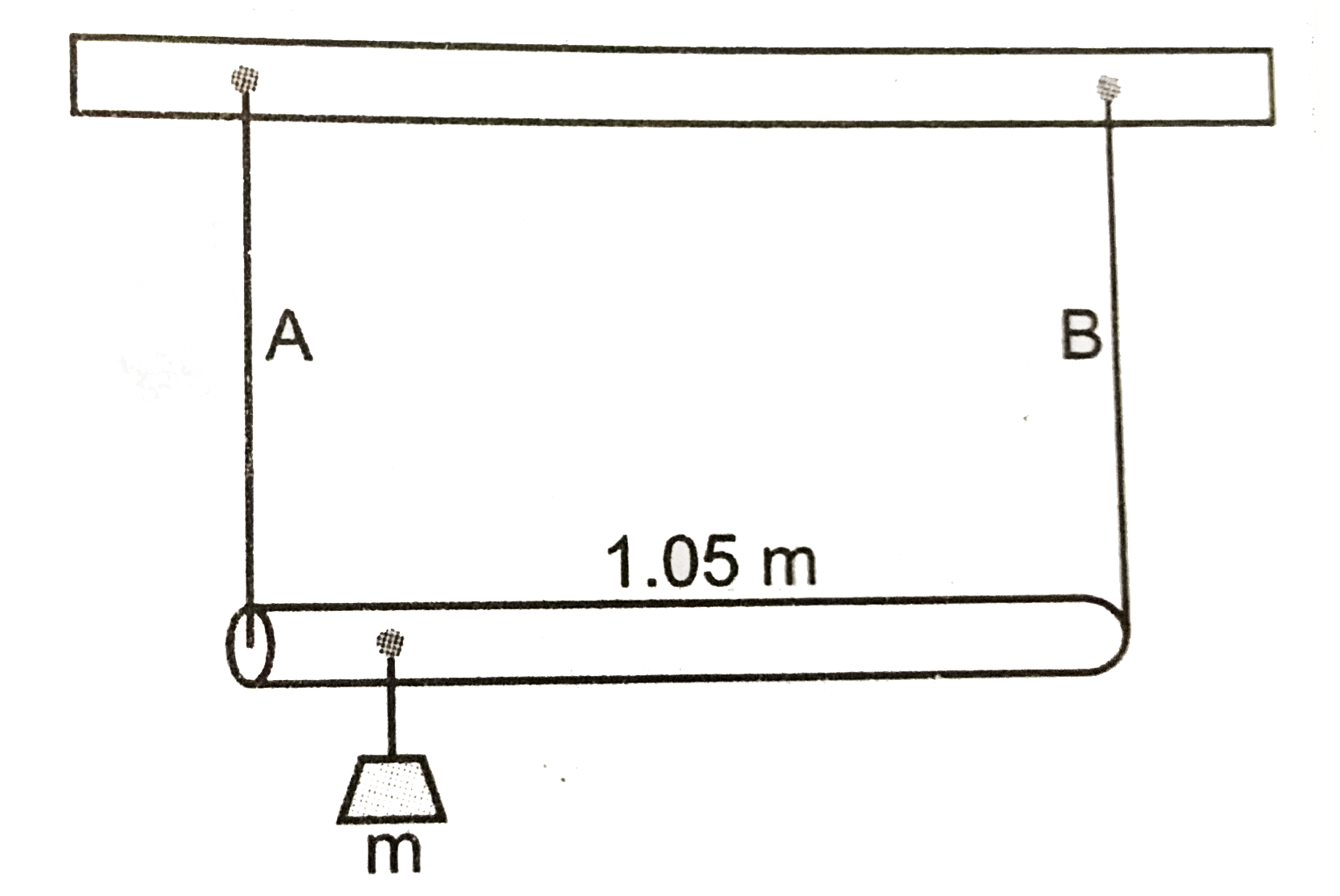
View Solution
