A steel wire of cross- section is held straight(but under no tension) by attaching it firmly to two points a distance apart at . If the temperature now decreases to and if the two points remain fixed, what will be the tension in the wire ? For steel, .
The correct Answer is:A, B
To solve the problem, we will follow these steps:
Step 1: Identify the given data
- Cross-sectional area of the steel wire, A=2.0mm2=2.0×10−6m2
- Initial length of the wire, L=1.50m
- Initial temperature, T1=30∘C
- Final temperature, T2=−10∘C
- Young's modulus for steel, Y=20.0000MPa=20×106Pa
- Coefficient of linear expansion for steel, α=13×10−6°C−1
Step 2: Calculate the change in temperature
ΔT=T2−T1=−10∘C−30∘C=−40∘C
Step 3: Calculate the change in length due to thermal contraction
The change in length (ΔL) can be calculated using the formula:
ΔL=L⋅α⋅ΔT
Substituting the values:
ΔL=1.50m⋅13×10−6°C−1⋅(−40∘C)
ΔL=1.50⋅13⋅(−40)×10−6m
ΔL=−0.00078m=−0.78mm
Step 4: Calculate the thermal stress in the wire
The thermal stress (σ) generated in the wire can be calculated using the formula:
σ=Y⋅ΔLL
Substituting the values:
σ=20×106Pa⋅−0.000781.50
σ=20×106⋅(−0.00052)Pa
σ=−10400Pa=−10.4kPa
Step 5: Calculate the tension in the wire
The tension (T) in the wire can be calculated using the formula:
T=σ⋅A
Substituting the values:
T=−10400Pa⋅2.0×10−6m2
T=−0.0208N
Final Answer
The tension in the wire due to the decrease in temperature is approximately 0.0208N (the negative sign indicates that it is a compressive force).
- Cross-sectional area of the steel wire, A=2.0mm2=2.0×10−6m2
- Initial length of the wire, L=1.50m
- Initial temperature, T1=30∘C
- Final temperature, T2=−10∘C
- Young's modulus for steel, Y=20.0000MPa=20×106Pa
- Coefficient of linear expansion for steel, α=13×10−6°C−1
ΔT=T2−T1=−10∘C−30∘C=−40∘C
The change in length (ΔL) can be calculated using the formula:
ΔL=L⋅α⋅ΔT
Substituting the values:
ΔL=1.50m⋅13×10−6°C−1⋅(−40∘C)
ΔL=1.50⋅13⋅(−40)×10−6m
ΔL=−0.00078m=−0.78mm
The thermal stress (σ) generated in the wire can be calculated using the formula:
σ=Y⋅ΔLL
Substituting the values:
σ=20×106Pa⋅−0.000781.50
σ=20×106⋅(−0.00052)Pa
σ=−10400Pa=−10.4kPa
The tension (T) in the wire can be calculated using the formula:
T=σ⋅A
Substituting the values:
T=−10400Pa⋅2.0×10−6m2
T=−0.0208N
The tension in the wire due to the decrease in temperature is approximately 0.0208N (the negative sign indicates that it is a compressive force).
Topper's Solved these Questions
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Single Correct
12 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 More Than One Correct
7 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 1 Objective
10 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary
30 Videos
- UNIT AND DIMENSIONSBOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason
2 Videos
Similar Questions
It takes 2.0 seconds for a sound wave to travel between two fixed points when the day temperature is 10∘C. If the temperature rise to 30∘C the sound wave travels between the same fixed parts in
View SolutionResistance of a metal wire of length 1 m is 26Ω at 20∘C. If the diameter of the wire is 0.3mm, what will be the resistivity of the metal at that temperature ? .
View SolutionA string of density 7.5gcm−3 and area of cross - section 0.2mm2 is stretched under a tension of 20 N. When it is plucked at the mid-point, the speed of the transverse wave on the wire is
View SolutionA steel wire 0.72 m long has a mass of 5.0×10−3 kg . If the wire is under a tension of 60 N, what is the speed of transverse waves on the wire ?
View SolutionA steel wire of original length 1m and cross-sectional area 4.00mm2 is clamped at the two ends so that it lies horizontally and without tension. If a load of 2.16kg is suspended from the middle point of the wire, what would be its vertical depression ?
Y of the steel =2.0×1011Nm−2. Take g=10ms−2
View SolutionA steel wire of length 2L and cross-section area A is stretched, wetl within elastic limit horizontally between two pillars, a mass m is suspended from the mid-point of wire such that depression at the middle is x. Strain in the wire is proportional to
View SolutionA mild steel wire of length 1.0m and cross sectional area 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is
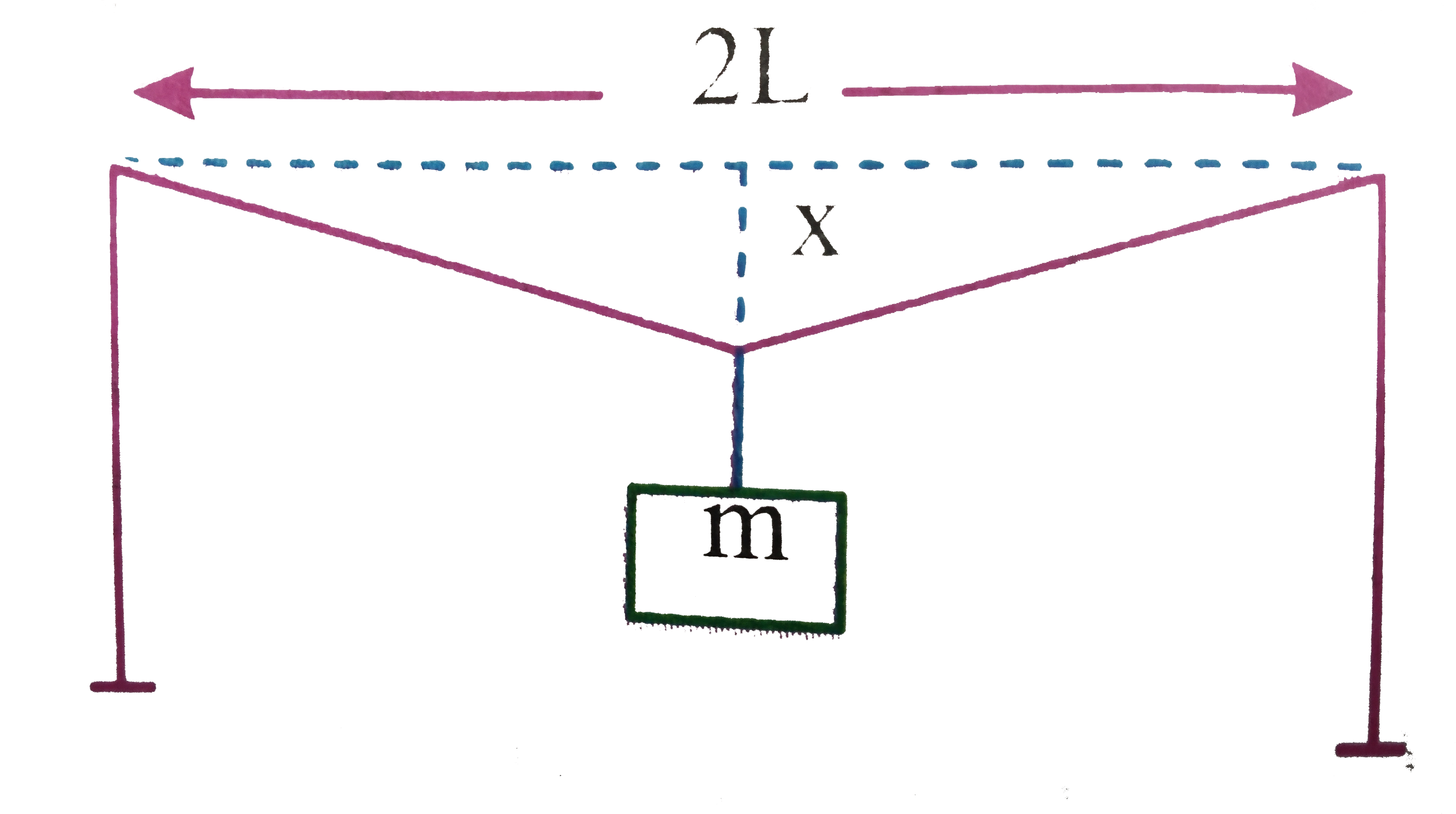
View SolutionA steel wire 2mm in diameter is just stretched between two rigid walls at 20°C. If the temperature falls to 10°C, find the tension in the wire. Linear coefficient of expansion of steel = 11×10−6/kandY=2×1011N/m2
View SolutionA steel wire of length 20 cm and uniform cross-section 1mm2 is tied rigidly at both the ends. If the temperature of the wire is altered from 40∘C to 20∘C, the change in tension. [Given coefficient of linear expansion of steel is 1.1×105.∘C−1 and Young's modulus for steel is 2.0×1011Nm−2]
View SolutionA steel rod is rigidly clamped at its two ends. The rod is under zero tension at 20∘C. If the temperature rises to 100∘C, what force will the rod exert on one of the clapms? Area of cross section of the rod =2.00mm2 . Coefficient of linear expansion of steel =12.0×10−6C−1 and Young's modulus of steel 2.00×1011Nm−2.
View Solution
