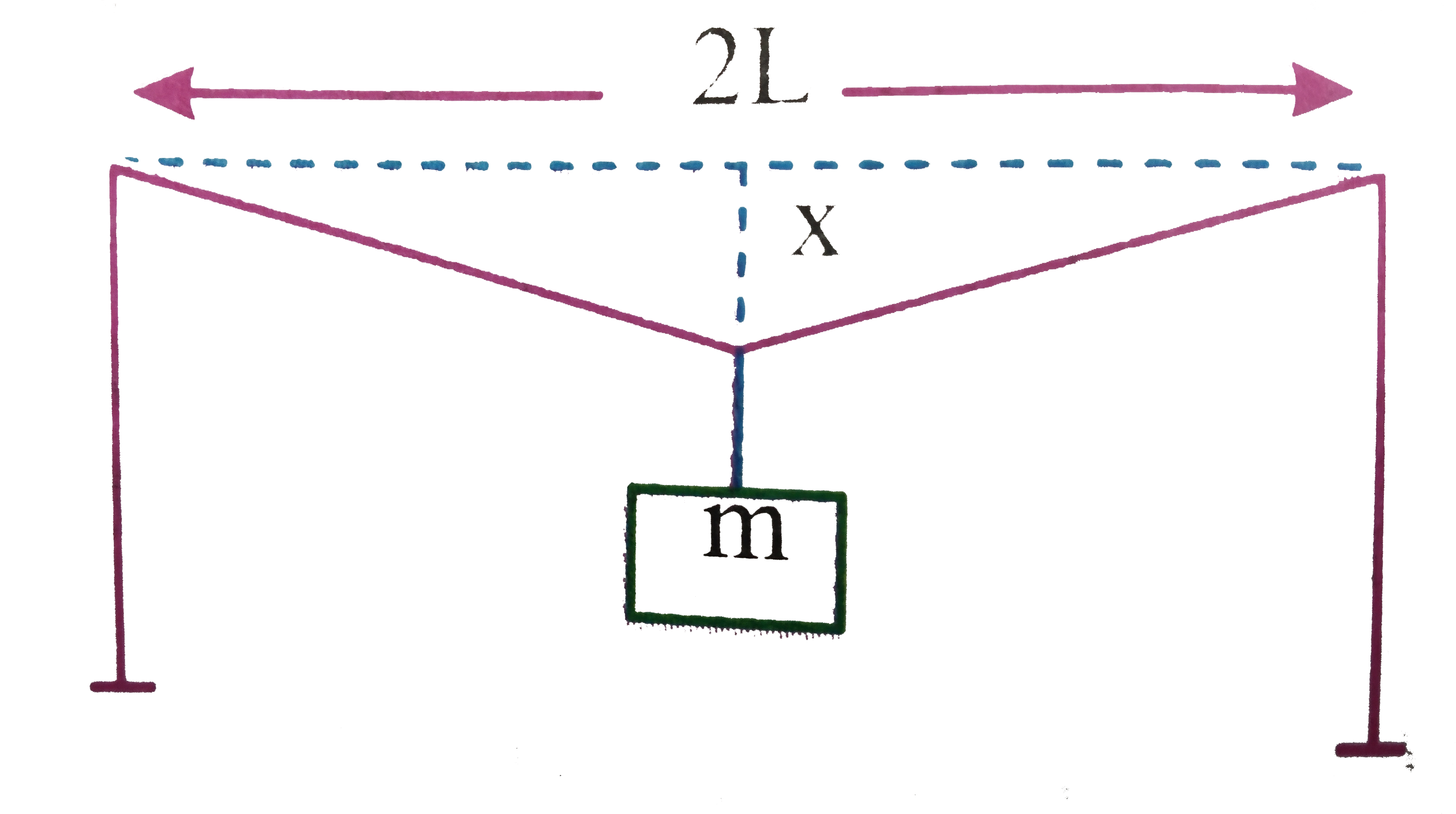
A steel wire of length 2L and cross-section area A is stretched, wetl within elastic limit horizontally between two pillars, a mass m is suspended from the mid-point of wire such that depression at the middle is x. Strain in the wire is proportional to
X2/l
X/L
X2/L2
X/L2
To solve the problem, we need to determine the strain in the steel wire when a mass m is suspended from its midpoint, causing a depression x at that point.
1. Understanding the Setup:
- The steel wire has a total length of 2L and is stretched horizontally between two pillars.
- A mass m is suspended at the midpoint of the wire, causing a downward depression x.
2. Identifying Lengths:
- When the mass is suspended, the wire forms two segments: each segment has a length of L (from the midpoint to each pillar).
- The new length of each segment, due to the depression, can be found using the Pythagorean theorem. The length of each segment becomes √L2+x2.
3. Calculating Change in Length:
- The original length of the wire between the two pillars is 2L.
- The total length of the wire after the mass is suspended is 2√L2+x2.
- The change in length ΔL is given by:
ΔL=2√L2+x2−2L
4. Simplifying the Change in Length:
- Factor out the common term:
ΔL=2(√L2+x2−L)
- Using the binomial approximation for small x (assuming x is small compared to L):
√L2+x2≈L(1+x22L2)
- Thus,
ΔL≈2(L(1+x22L2)−L)=2L(x22L2)=x2L
5. Calculating Strain:
- Strain ϵ is defined as the change in length per unit original length:
Strain=ΔLOriginal Length=ΔL2L
- Substituting ΔL:
Strain=x2L2L=x22L2
6. Conclusion:
- The strain in the wire is proportional to x22L2.
Final Answer:
The strain in the wire is proportional to x22L2.
- The steel wire has a total length of 2L and is stretched horizontally between two pillars.
- A mass m is suspended at the midpoint of the wire, causing a downward depression x.
- When the mass is suspended, the wire forms two segments: each segment has a length of L (from the midpoint to each pillar).
- The new length of each segment, due to the depression, can be found using the Pythagorean theorem. The length of each segment becomes √L2+x2.
- The original length of the wire between the two pillars is 2L.
- The total length of the wire after the mass is suspended is 2√L2+x2.
- The change in length ΔL is given by:
ΔL=2√L2+x2−2L
- Factor out the common term:
ΔL=2(√L2+x2−L)
- Using the binomial approximation for small x (assuming x is small compared to L):
√L2+x2≈L(1+x22L2)
- Thus,
ΔL≈2(L(1+x22L2)−L)=2L(x22L2)=x2L
- Strain ϵ is defined as the change in length per unit original length:
Strain=ΔLOriginal Length=ΔL2L
- Substituting ΔL:
Strain=x2L2L=x22L2
- The strain in the wire is proportional to x22L2.
The strain in the wire is proportional to x22L2.
Topper's Solved these Questions
Similar Questions
A mild steel wire of length 1.0m and cross sectional area 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is
View SolutionA mild steel wire of length 1.0 m and cross-sectional are 0.5×10−2cm2 is streached, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid point of the wire, calculate the depression at the mid point.
g=10ms−2,Y=20×1011Nm−2.
View Solution
Knowledge Check
A mild steel wire of length 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is
 Ax22L2BxLCx2LDx22L
Ax22L2BxLCx2LDx22LA wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the force constant of the wire is
AYLABYlACYALDYAlA metal wire of length L1 and area of cross section A is attached to a rigid support. Another metal wire of length L2 and of the same cross sectional area is attached to the free end of the first wire. A body of mass M is then suspended from the free end of the second wire, if Y1 and Y2 are the Young's moduli of the wires respectively the effective force constant of the system of two wires is
A[(Y1Y2)A][2(Y1L2+Y2L1)]B[(Y1Y2)A](L1L2)2C[(Y1Y2)A](Y1L2+Y2L1)D[(Y1Y2)1/2A](L2+L1)1/2
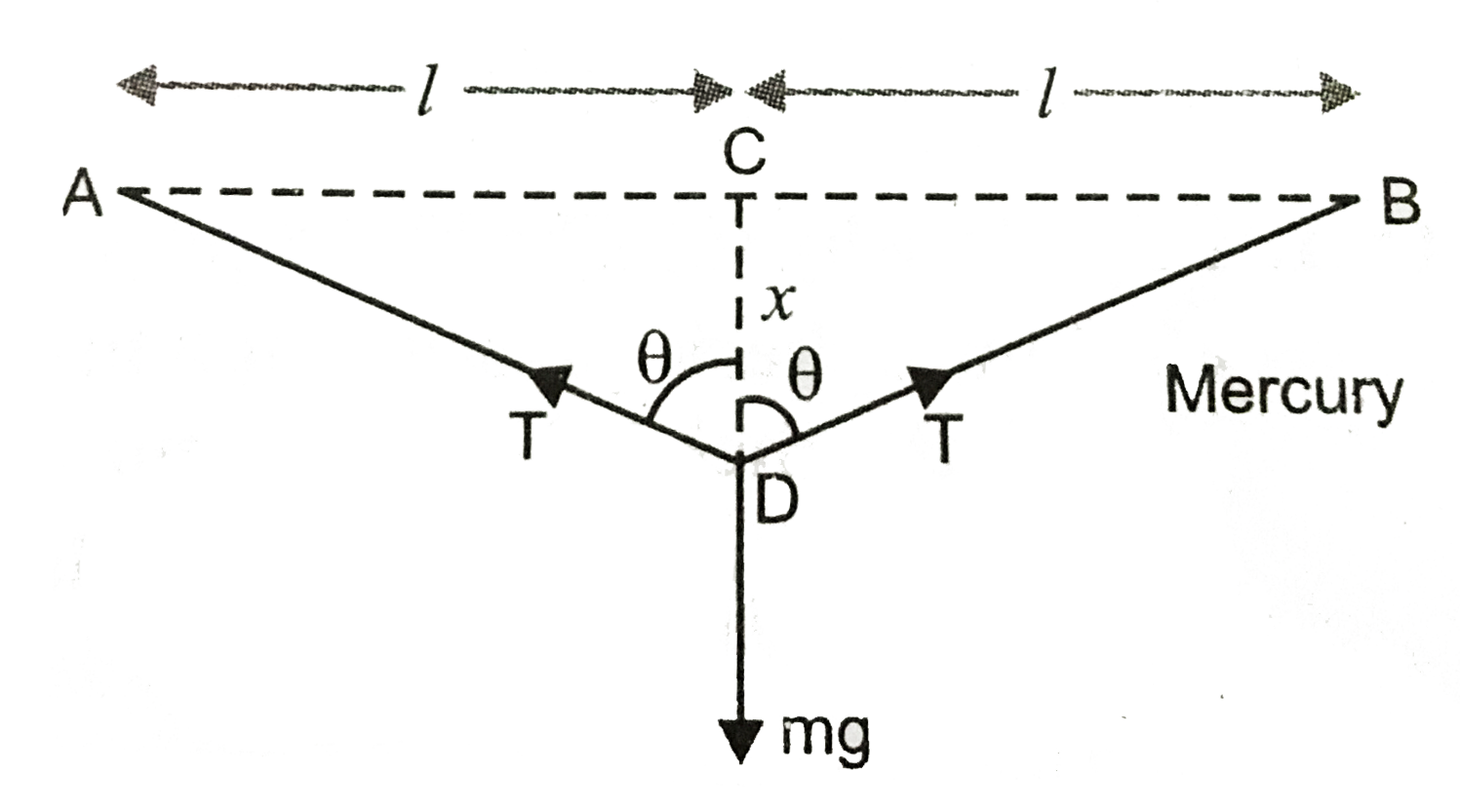
A wire of cross section A is stretched horizontally between two clamps located 2lm apart. A weight Wkg is suspended from the mid-point of the wire. If the mid-point sags vertically through a distance x<l, the strain produced is
View SolutionA steel wire of original length 1m and cross-sectional area 4.00mm2 is clamped at the two ends so that it lies horizontally and without tension. If a load of 2.16kg is suspended from the middle point of the wire, what would be its vertical depression ?
Y of the steel =2.0×1011Nm−2. Take g=10ms−2
View SolutionA steel wire of negligible mass, length 2I, cross sectional area 'A' and Young's modulus 'Y' is held between two rigid walls. A small body of mass 'm' is suspended from its middle point 'O' as shown. The vertical descent of the middle point 'O' of the wire is

View SolutionA mass m is suspended from a wire . Change in length of the wire is Δl. Now the same wire is stretched to double its length and the same mass is suspended from the wire. The change in length in this case will become (it is suspended that elongation in the wire is within the proportional limit)
View SolutionA metal wire of length L1 and area of cross section A is ttached to a rigid support. Another metal wire of length L2 and of the same cross sectional area is attached to the free end of the first wire. A body of mass M is then suspended from the free end of the second wire, if Y1 and Y2 are the Young's moduli of the wires respectively the effective force constant of the system of two wires is
View Solution
