A steel wire of length 4.5 m and cross-sectional area 3×10−5m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4x10−5m2 under a given load. The ratio of the Young's modulus of steel to that of copper is
1.3
1.5
1.7
1.9
The correct Answer is:C
To find the ratio of the Young's modulus of steel to that of copper, we can follow these steps:
Step 1: Understand the given information
We have two wires:
- Steel wire: Length Ls=4.5m, Cross-sectional area As=3×10−5m2
- Copper wire: Length Lc=3.5m, Cross-sectional area Ac=4×10−5m2
Both wires stretch by the same amount under the same load.
Step 2: Write the formula for Young's modulus
The Young's modulus Y is defined as:
Y=StressStrain=F/AΔL/L
where:
- F is the force applied,
- A is the cross-sectional area,
- ΔL is the extension (stretch),
- L is the original length of the wire.
Step 3: Set up the equations for both wires
For the steel wire:
Ys=FAs⋅LsΔL
For the copper wire:
Yc=FAc⋅LcΔL
Step 4: Relate the two Young's moduli
Since both wires stretch by the same amount (ΔL) and are subjected to the same force (F), we can set up the ratio:
YsYc=AcAs⋅LsLc
Step 5: Substitute the values
Substituting the values we have:
- Ac=4×10−5m2
- As=3×10−5m2
- Ls=4.5m
- Lc=3.5m
Now substituting these into the ratio:
YsYc=4×10−53×10−5⋅4.53.5
Step 6: Simplify the expression
The 10−5 cancels out:
YsYc=43⋅4.53.5
Calculating 4.53.5:
4.53.5=4535=97
Now substituting back:
YsYc=43⋅97=3621=127≈1.714
Step 7: Conclusion
Thus, the ratio of the Young's modulus of steel to that of copper is approximately:
YsYc≈1.7
Final Answer
The ratio of the Young's modulus of steel to that of copper is ≈1.7.
---
We have two wires:
- Steel wire: Length Ls=4.5m, Cross-sectional area As=3×10−5m2
- Copper wire: Length Lc=3.5m, Cross-sectional area Ac=4×10−5m2
The Young's modulus Y is defined as:
Y=StressStrain=F/AΔL/L
where:
- F is the force applied,
- A is the cross-sectional area,
- ΔL is the extension (stretch),
- L is the original length of the wire.
For the steel wire:
Ys=FAs⋅LsΔL
Yc=FAc⋅LcΔL
Since both wires stretch by the same amount (ΔL) and are subjected to the same force (F), we can set up the ratio:
YsYc=AcAs⋅LsLc
Substituting the values we have:
- Ac=4×10−5m2
- As=3×10−5m2
- Ls=4.5m
- Lc=3.5m
YsYc=4×10−53×10−5⋅4.53.5
The 10−5 cancels out:
YsYc=43⋅4.53.5
4.53.5=4535=97
YsYc=43⋅97=3621=127≈1.714
Thus, the ratio of the Young's modulus of steel to that of copper is approximately:
YsYc≈1.7
The ratio of the Young's modulus of steel to that of copper is ≈1.7.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - APPLICATIONS OF ELASTIC BEHAVIOUR OF MATERIALS
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - HOTS
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - STRESS-STRAIN CURVE
5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar
5 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A steel wire of length 4.7m and cross-sectional area 3×10−6m2 stretches by the same amount as a copper wire of length 3.5m and cross-sectional area of 4×10−6m2 under a given load. The ratio of Young's modulus of steel to that of copper is
View SolutionA steel wire of length 4.7 m and cross-section 3.0×102m2 stretches by the same amount as a copper wire of length 3.5 m and cross-section 4.0xx102m2 under a given load. What is the ratio of the Young.s modulus of steel to that of copper?
View Solution
Knowledge Check
A wire of length L and cross-sectional area A is made of a material of Young's modulus Y. IF the wire is stretched by an amount x, the workdone is
AYAx22LBYAx2L2CYAx2LDYAx2L
A steel wire of length 4.7m and cross-section 3.0×10−5m2 stretched by the same amount as a copper wire of length 3.5m and cross-section 4.0×10−5m2 under a given load. What is the ratio of Young's modulus of steel to that of copper ?
View Solution
A steel wire of length 60 cm and area of cross section 10−6m2 is joined with a n aluminium wire of length 45 cm and are of cross section 3×10−6m2. The composite string is stretched by a tension of 80 N. Density of steel is 7800kgm−3 and that of aluminium is 2600kgm−3 the minimum frequency of tuning fork. Which can produce standing wave in it with node at joint is
View SolutionCalculate the force required to incrase the length of wire of cross-sectional area 10−6m2 by 50% if the Young's modulus of the material of the wire is 90×109Pa.
View SolutionA brass of length 2m and cross-sectional area 2.0cm2 is attached end to end to a steel rod of length and cross-sectional area 1.0cm2. The compound rod is subjected to equal and oppsite pulls of magnitude 5×104N at its ends. If the elongations of the two rods are equal, the length of the steel rod (L) is
{YBrass=1.0×1011N/m2 and Ysteel=2.0×1011N/m2
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
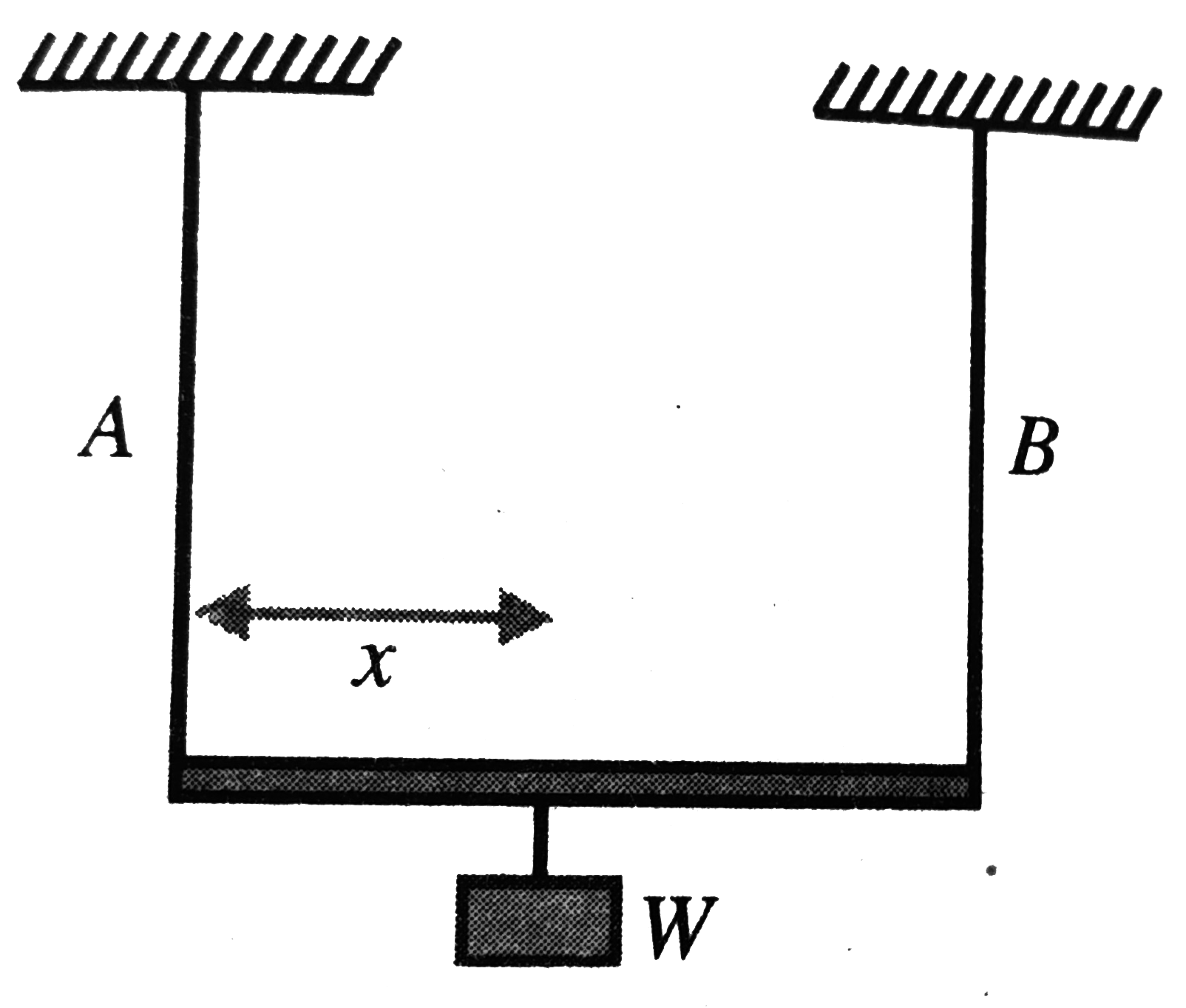
Determine the value of x so that equal stresses are produced in each wire.
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
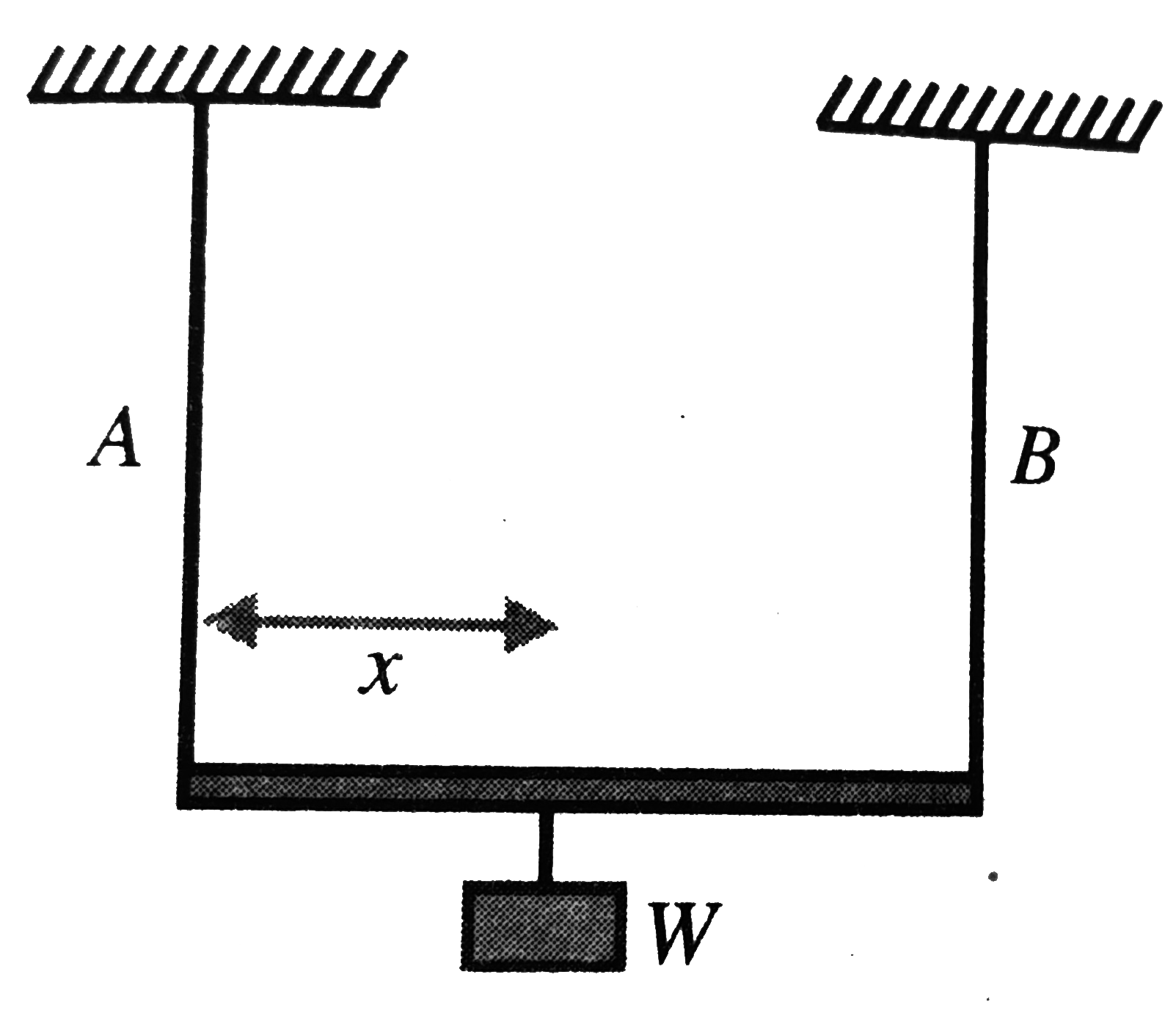
Determine the value of x so that equal strains are produced in each wire
View SolutionA steel wire of length l and cross sectional area A is stretched by 1 cm under a given load. When the same load is applied to another steel wire of double its length and half of its cross section area, the amount of stretching (extension) is
View Solution
