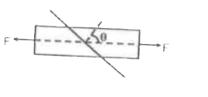
A bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle θ with length. The ratio of tensile stress to the shearing stress on the plane BB' is
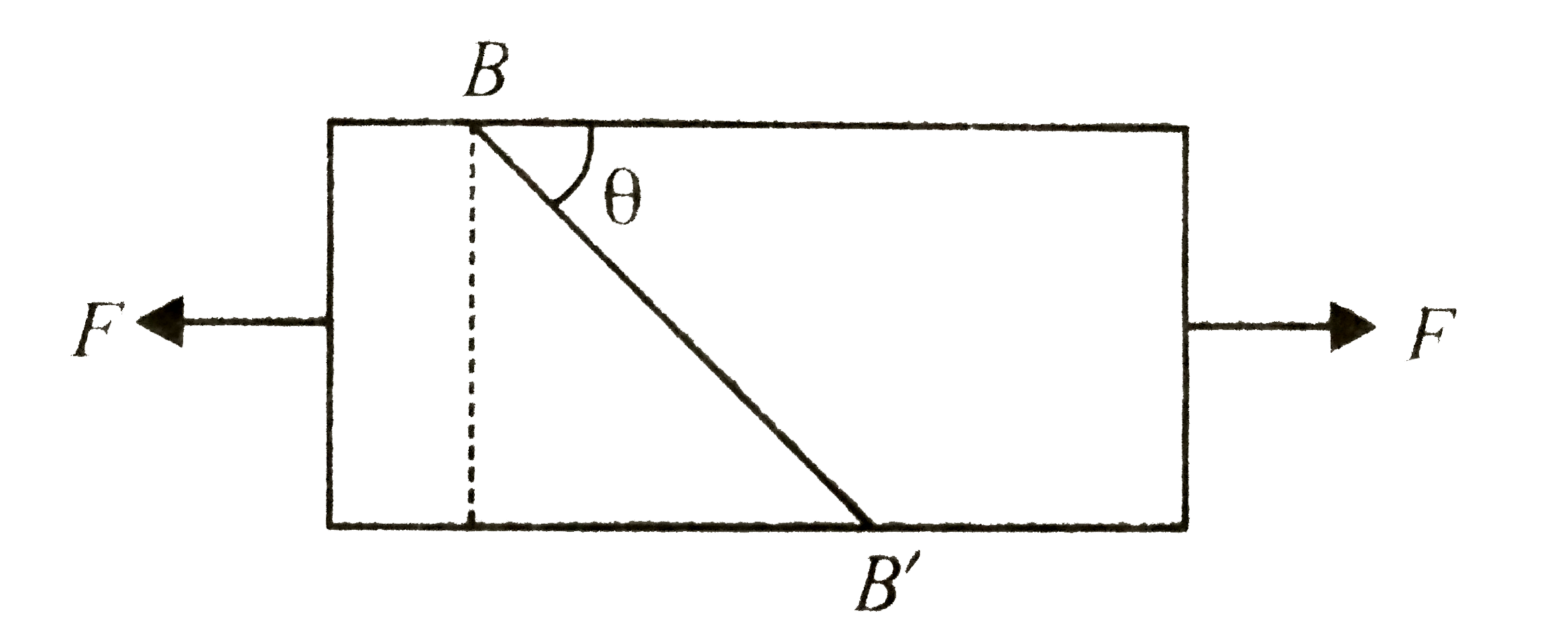
1. tanθ
2. secθ
3. cotθ
4. cosθ
The correct Answer is:A
Consider the equilibrium of the palne BB.
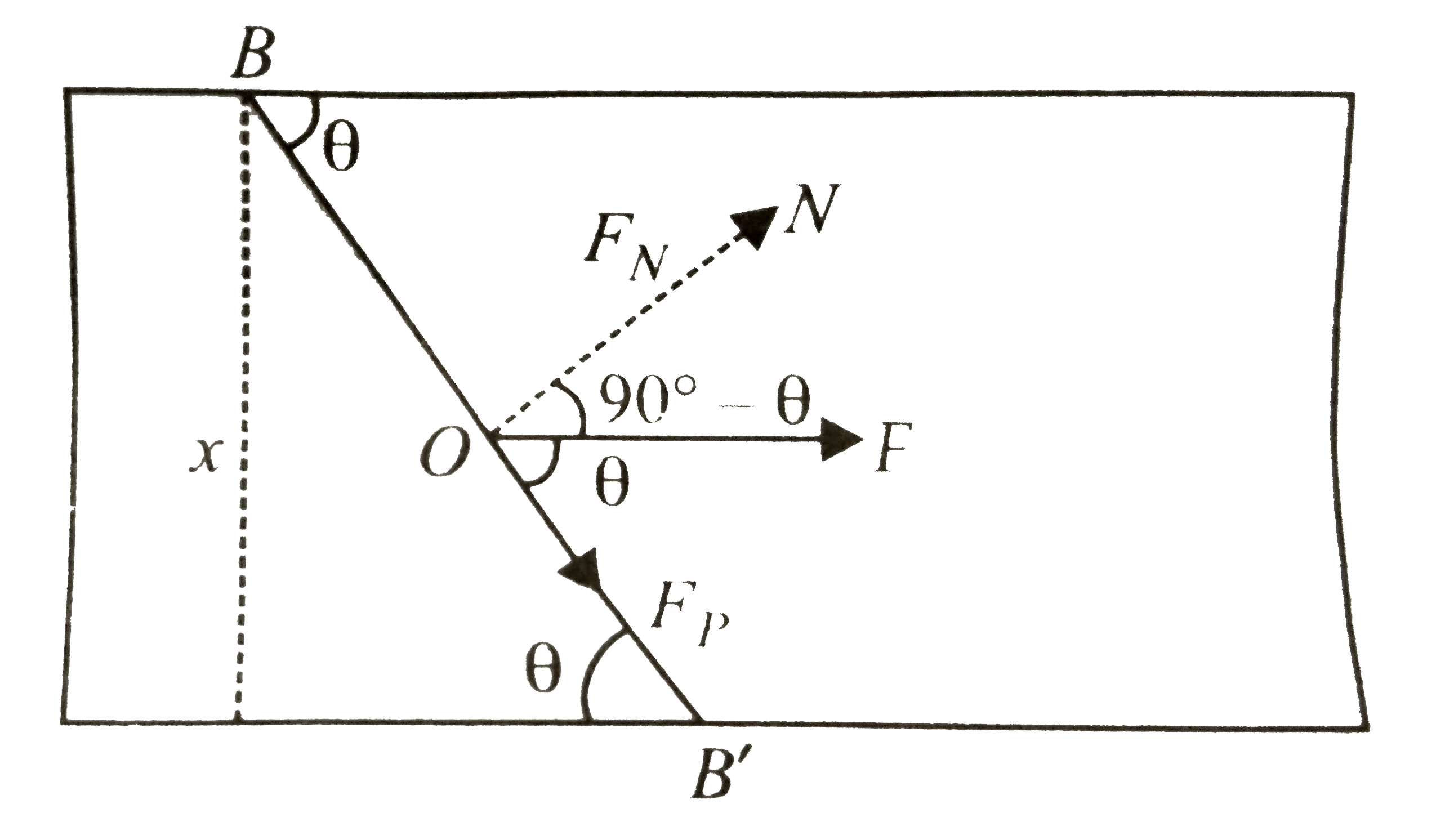
A force F must be acting on this on this plane making an angle (90∘−θ) with the normal ON. Resolving F into two components, along the palne and normal to the plane.
Component of force F along the palne, Fp=Fcosθ Component of force F normal to the palne ,
FN=Fcos(90∘−θ)=Fsinθ
Let the are of the face BB be A . Then AA=sinθ
∴A'=Asinθ
∴ Tensile strss =FsinθθA'=FAsin2θ
Shearing stress =FcosθA'=FAcosθsinθ=Fsinθ2A
Their corresponding ratio is
Tensile stressShearing stress=FAsin2θ×AFsinθcosθ=tanθ
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - APPLICATIONS OF ELASTIC BEHAVIOUR OF MATERIALS
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - HOTS
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - STRESS-STRAIN CURVE
5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar
5 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.
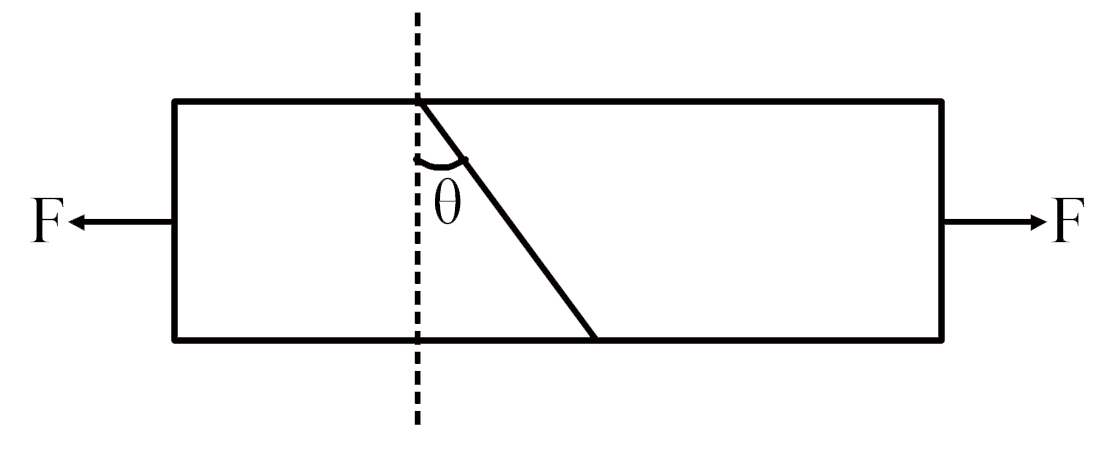
The tensile stress at this plane in terms of F, A and θ is
View SolutionA bar of cross section A is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar.

a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of θ is the tensile stress maximum?
d. For what value of θ is the shearing stress maximum?
View SolutionA bar of cross-section A is subjected to equal and opposite tensile forces at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar .
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of θ is the tensile stress maximum
(iv) For what value of θ is the shearing stress maximum?
View SolutionA bar of cross-section A is subjected two equal and opposite tensile forces at its ends consider a plane section of the bar whose makes an angle θ with the axis of the bar.
(a) what is the tensile stress on this plane ?
(b)what is the shearing stress on this plane ?
(c )for what value of θ is the tensile stress is maximum ?
(d) for what value of θ is the shearing stress maximum ?
View SolutionConsider a long steel bar under a tensile stress due to forces F, acting at the edges along the length of the bar

Consider a plane making an angle θ with the length. What are the tensile and shering stresses on this plane ? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?
View SolutionA rod area of cross section A is being acted upon by two forces F - F as shown in figure. Consider a section ab of rod whose normal makes angle θ with horimontal. The shear stress upon this section is maximum when θ=180∘n. Find n.

View SolutionA massless uniform rod is subjected to froce F at its free end as shown in figure. The ratio of tensile stress at plane P1 to stress at P2 is
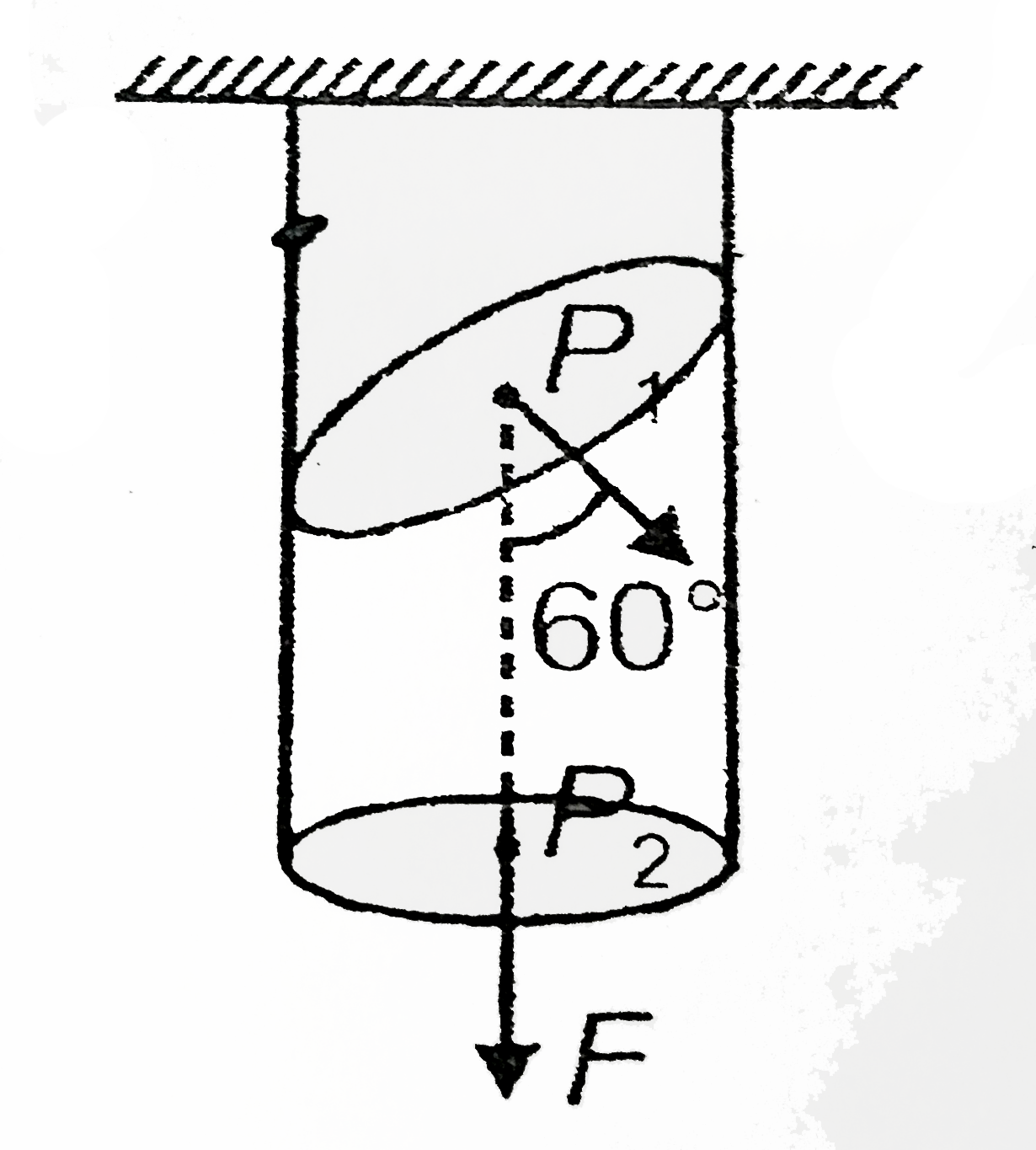
View SolutionA copper rod with length 1.4 m and area of cross-section of 2cm2 is fastened to a steel rod with length L and cross-sectional area 1cm2. The compound rod is subjected to equal and opposite pulls to magnitude 6.00×104 N at its ends .
(a) Find the length L of the steel rod if the elongation of the two rods are equal .
(b) What is stress in each rod ?
(c ) What is the strain in each rod ? [Ysteel=2×1011Pa,YCu=1.1×1011Pa]

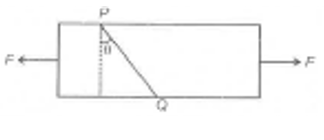
View SolutionA long rod of steel under a tensile stress due to the force acting on the edges along the length. The value of angle 0 for which shearing stress is maximum is
View SolutionFind the moment of inertia of a section of circular disc of radius R about an axis perpendicualr to its plane as shown in the figure. The section has mass m and subtends an angle θ at the centre.
View Solution
