A stiff wire is bent into a cylinder loop of diameter D. It is clamped by knife edges at two points opposite to each other . A transverse wave is sent around the loop by means resonance frequency (fundamental mode) of the loop in terms of wave speed v and diameter D is
vD
2vπD
vπD
v2πD
The correct Answer is:C
To find the fundamental mode of resonance frequency of a stiff wire bent into a cylindrical loop of diameter D, we can follow these steps:
Step 1: Determine the Length of the Wire
The wire is bent into a circular loop, so the length of the wire L is equal to the circumference of the circle. The circumference C of a circle is given by the formula:
C=πD
Thus, the length of the wire L is:
L=πD
Step 2: Identify the Boundary Conditions
The wire is clamped at two points opposite each other. These points act as nodes for the standing wave. In the fundamental mode of resonance, there is one complete wave (one loop) between the two nodes.
Step 3: Relate Wavelength to Length
In the fundamental mode, the length of the wire corresponds to half the wavelength λ:
L=λ2
Substituting the expression for L:
πD=λ2
From this, we can solve for the wavelength λ:
λ=2πD
Step 4: Use the Wave Speed Relation
The relationship between wave speed v, frequency f, and wavelength λ is given by:
v=fλ
We can rearrange this to find the frequency:
f=vλ
Step 5: Substitute for Wavelength
Now, substituting the expression for λ into the frequency equation:
f=v2πD
Conclusion
Thus, the fundamental mode of resonance frequency of the loop in terms of wave speed v and diameter D is:
f=v2πD
The wire is bent into a circular loop, so the length of the wire L is equal to the circumference of the circle. The circumference C of a circle is given by the formula:
C=πD
Thus, the length of the wire L is:
L=πD
The wire is clamped at two points opposite each other. These points act as nodes for the standing wave. In the fundamental mode of resonance, there is one complete wave (one loop) between the two nodes.
In the fundamental mode, the length of the wire corresponds to half the wavelength λ:
L=λ2
Substituting the expression for L:
πD=λ2
From this, we can solve for the wavelength λ:
λ=2πD
The relationship between wave speed v, frequency f, and wavelength λ is given by:
v=fλ
We can rearrange this to find the frequency:
f=vλ
Now, substituting the expression for λ into the frequency equation:
f=v2πD
Thus, the fundamental mode of resonance frequency of the loop in terms of wave speed v and diameter D is:
f=v2πD
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Multiple26videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Assertion - Reasoning6videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Subjective24videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - 241videos
THERMODYNAMICS
Similar Questions
A thin insulating wire is stretched·along the diameter of an. insulated circular hoop of radius R. A small bead of mass m and charge-q is threaded onto the wire. Two small identical charges are tied to the hoop at points opposite to each other, so that the diameter passing through them is perpendicular to the thread as shown in figure. The bead is released at a point which.is located at a distance x0 from the centre of the hoop. Assume that x0<<R.
(a) What is the resultant force acting on the charged bead?
(b) Describe the motion of the bead after it is released X
(c) Use the assumption that xR<<1 to obtain an approximate equation of motion, and find the displacement and velocity of the bead as functions of time
(d) When will the velocity of the bead will bcome zero for the first time?
 View Solution
View SolutionConsider two thin identical conducting wires covered with very thin insulating material.One of the wires is bent into a loop and produces magnetic field B1 at its centre when a current I passes through it.The second wire is bent into a coil with three identical loops adjacent to each other and produces magnetic field B2 at the centre of the loops when current "I/3" passes through it.The ratio B1:B2 is: (a) 1:3 (b) 9:1 (c) 1:9 (d) 1:1
View Solution
Knowledge Check
- Question 1 - Select One
A vibrating sonometer wire in resonance with a tuning fork of frequency 150 Hz. If only loop is formed on the wire and the length of one loop is 40 cm, then the velocity of transverse waves on the wire will be
Aa. 120m/sBb. 240m/sCc. 90m/sDd. 60m/s - Question 2 - Select One
The figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
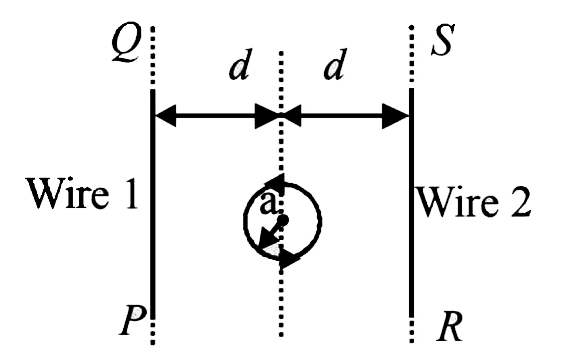
(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that caseA(a) current in wire 1andwire2 in the direction PQandRS, respectively and h≈aB(b) current in wire 1andwire2 in the direction PQandSR, respectively and h≈aCcurrent in wire 1andwire2 in the direction PQandSR, respectively and h≈1.2aDcurrent in wire 1andwire2 in the direction PQandRS, respectively and h≈1.2a - Question 3 - Select One
The figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.

(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that caseAμ0I2a2dBμ0I2a22dC√3μ0I2a2dD√3μ0I2a22d
A steel wire of diameter d=1.0mm is stretched horizontally between two clamps located at the distance l=2.0m from each other. A weight of mass m=0.25kg is suspended from the mid-point O of the wire. What will the resulting descent of the point O be in centrimetres?
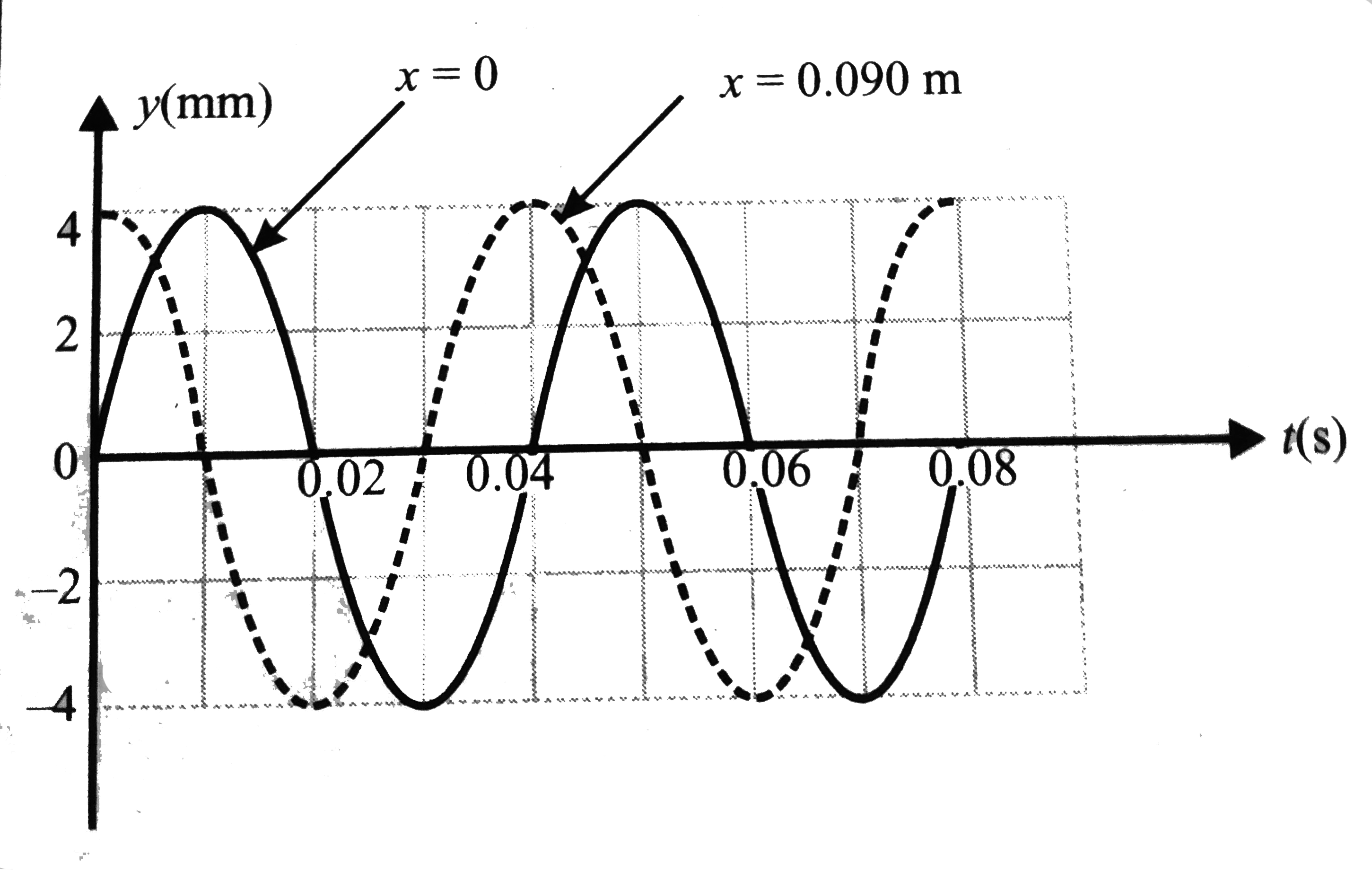
View SolutionA sinusoidal wave is propagating along a streched string that lies along the x-axis. The displacement of the string as a function of time is graphed in for particles at x-0 and at x=0.0900 m. (a) what is the amplitude of the wave? (b)what is the period of the wave? (c ) you are told that the two points x=0 and x=0.0900 m are within one wavelength of each other. if the wave is moving in the +x-direction, determine the wavelength and the wave speed. (d) if instead the wave is moving in the -x-direction, determine the wavelength and the wave speed. (e) would it be possible to derermine definitely the wavelength in parts (c ) and (d) if you were not told that the two points were within one wavelength of each other? why ot why not?
 View Solution
View SolutionA thin insulating wire is stretched along the diameter of an insulated circular hoop of radius E. A small bead of mass m and charge –q is threaded onto the wire. Two small identical charge= are tied to the hoop at points opposite to each other, so that the diameter passing throughtheL-is perpendicular to the thread (see figure). The bead is released at a point which is a distance-, from the centre of the hoop. Assume that x0<<R.
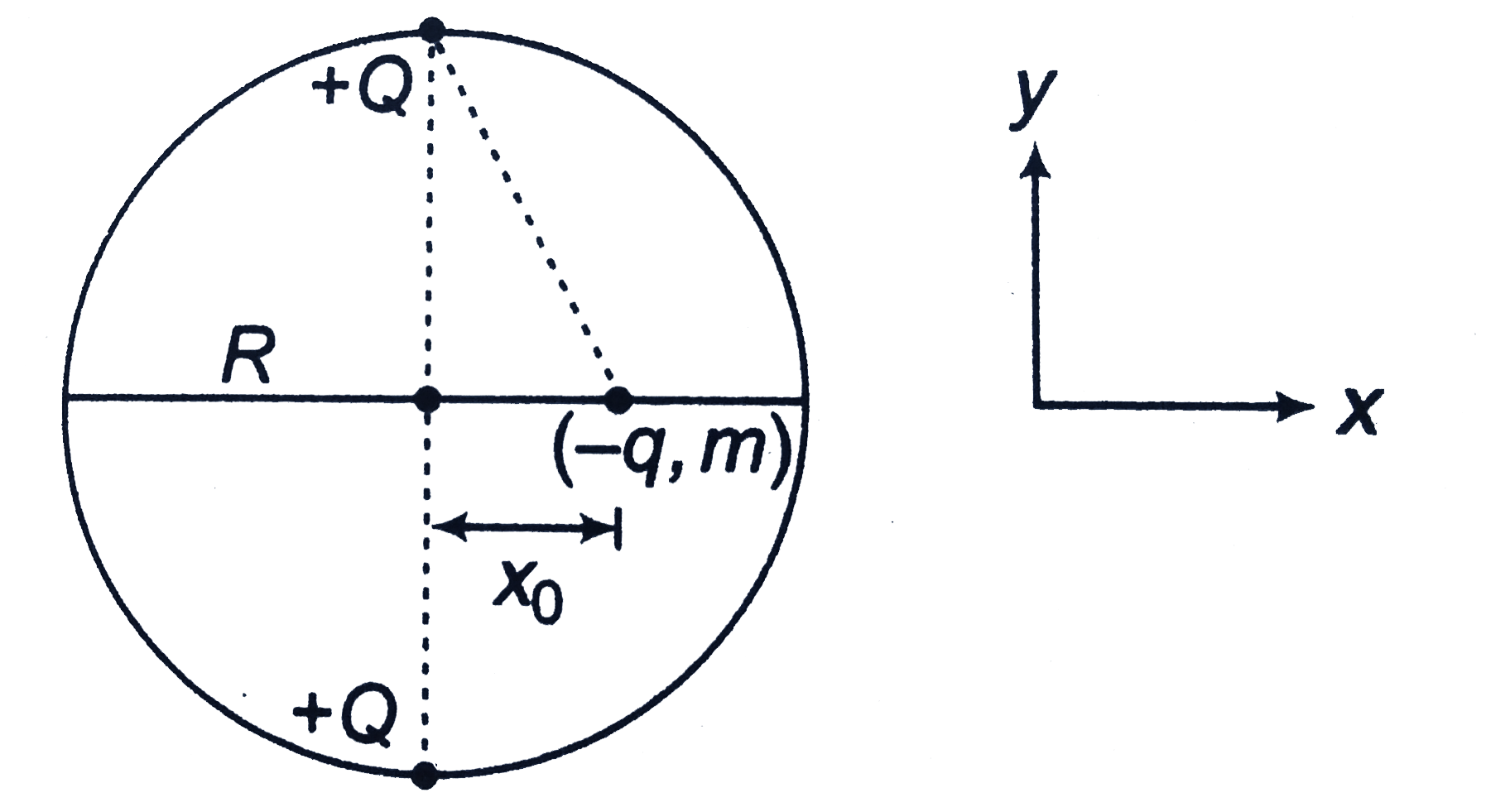
a. What is the resultant acting on the charged bead?
b. Describe (qualitatively) the motion of the bead after it is released.
c. Use the assumption that x/R<<1 to obtain an approximate equation of motinand find the dislacemet ad velocity of the bead as functuions of time.
d. When will the velocity of the bead will become zero for the first time?View SolutionA wire with mass 40.0 g is stretched so that its ends are tied down at points 80.0 cm apart.The wire vibrates in its fundamental mode with frequency 60.0 Hz and with an amplitude at the antinodes of 0.300 cm.
(a) What is the speed of propagation of transverse wave in the wire?
Compute the tension in the wire.
(c) Find the maximum transverse velocity and acceleration of particles in the wire.View SolutionA circular insulated copper wire loop is twisted to form two loops of are A and 2A as shown in the figure. At the point of crossing the wires remain electrically insulated from each other. The entire loop lies in the plane ( of the paper). A uniform magnetic →B point into the plane of the paper . At t=0, the loop starts rotation about the common diameter as axis with a constant angular velocity ω in the magnetic field. Which of the following options is /are correct ?
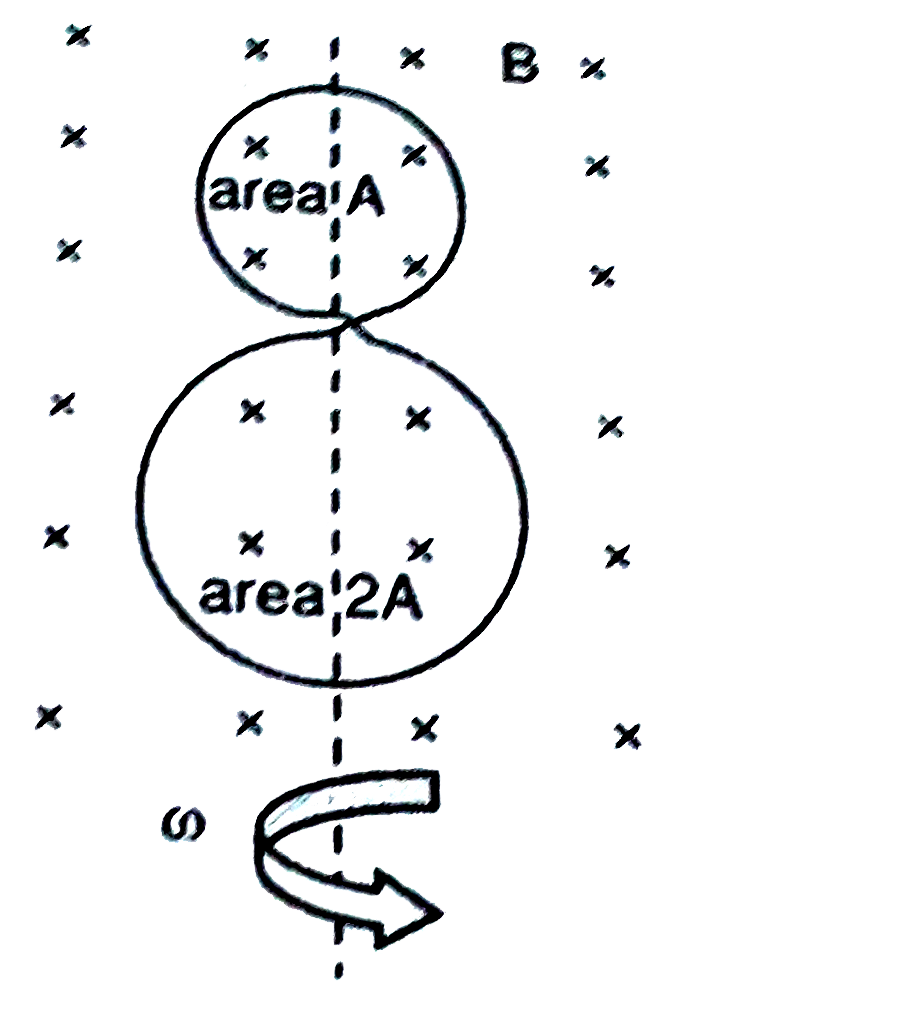 View Solution
View Solution

