A thin insulating wire is stretched along the diameter of an insulated circular hoop of radius E. A small bead of mass m and charge –q is threaded onto the wire. Two small identical charge= are tied to the hoop at points opposite to each other, so that the diameter passing throughtheL-is perpendicular to the thread (see figure). The bead is released at a point which is a distance-, from the centre of the hoop. Assume that x0<<R.
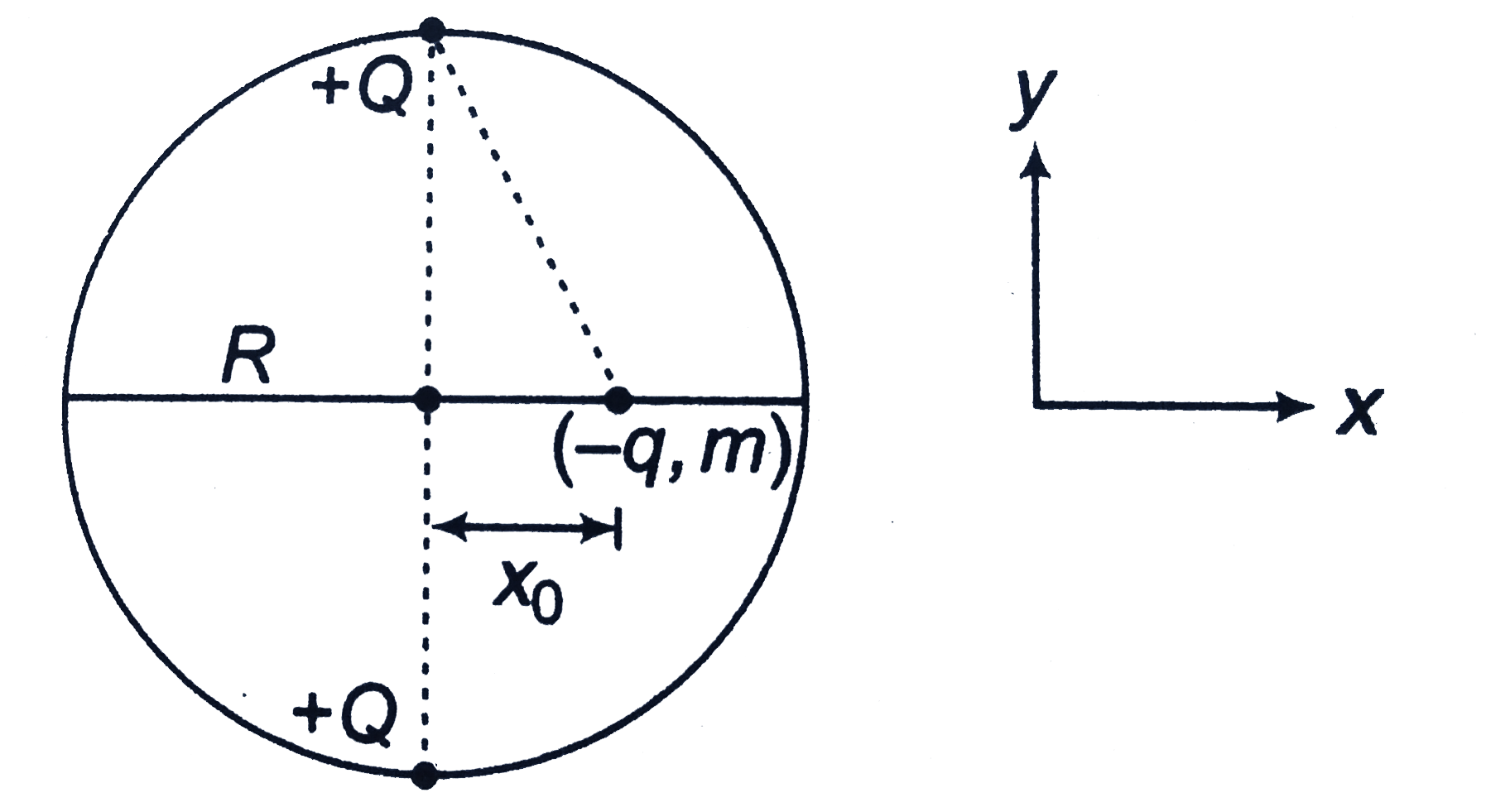
a. What is the resultant acting on the charged bead?
b. Describe (qualitatively) the motion of the bead after it is released.
c. Use the assumption that x/R<<1 to obtain an approximate equation of motinand find the dislacemet ad velocity of the bead as functuions of time.
d. When will the velocity of the bead will become zero for the first time?
The correct Answer is:A, B, C, D
a. Fnet=2Fcosθ
=2kQ.q√R2+x202.x0√(R2+x20)(Here,k=14πε0
=2kQqx0(R2+x20)32

We can generalised the force by putting x0=x we have
F=−2kQqx(R2+x2)32
Motion of bead will be periodic between
x=±x0
c. for x/Rltlt1, R^2+x^2=R^2<br>or F=-((2kQq)/R^3)xor a=F/m=-((2kQq)/(mR^3))x<br>sinceaprop-xmotionwillbesimp≤ha.rmonic∈nature.<br>Compar∈gwitha=-omea^2x, omega=sqrt((2kQq)/(mR^3))<br>x=x_0cos omegat(asthepartic≤⋆tsformextremeposition)<br>v=(dx)/(dt)=-omegax_0sinomegat<br>d.Velociytwilbecomezeroatt=T/2=pi/omega<imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_VOL_4_C24_E01_214_S02.pngwh=80%mx-autosty≤=background:white;><br>ort=pisqrt((mR^3)/(2kQq))
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.1
10 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.2
15 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
Similar Questions
Which of the following is correct regarding electric charge ?
(i) If a body is having positive charge i.e. shortage of electrons.
(ii) If a body is having negative charge i.e. excess of electrons.
(iii) Minimum possible charge =±1.6×10−19C.
(iv) Charge is quantised i.e. Q=±ne,
where n=1,2,3,4....
View SolutionThere are two charge +1μc and +2μc kept at certain separation ,the ratio of electrostatic forces acting on them will be in the ratio
View SolutionTwo concentric conducting shells A and B are of radii R and 2R. A charge +q is placed at the centre of the shells. Shell B is earthed and a charge q is given to shell A. Find the charge on outer surface of A and B.
View SolutionA capacitor of 2μF is charged as shown in the figure. When the switch S is turned to position 2, the percentage of its stored energy dissipated is

View SolutionAn infinite number of particles each of mass m are placed on the positive X-axis of 1m,2m,4m,8m,... from the origin. Find the magnitude of the resultant gravitational force on mass m kept at the origin.
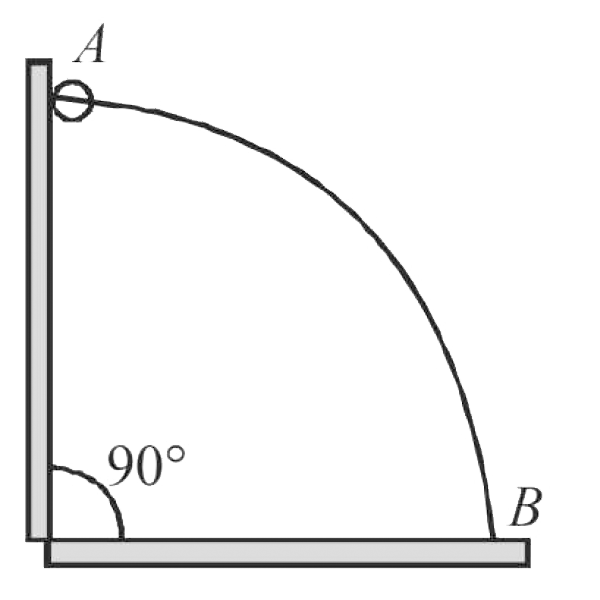
View SolutionA wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
View SolutionTwo small balls, each having charge q, are suspended by two insulating threads of equal length L fron a hook in an elevator. The elevator is freely falling. Calculate the angle etween the two threads and tension in each thread.
View SolutionTwo small beads having positive charges 3q and q are fixed at the opposite ends of a horizontal, insulating rod, extending from the origein to the point x=d as shown in fig. A third small charged bead is free to slide on the rod. At what position is the third bead in equilibrium? Can it be in stable eqyilibrium ?
View SolutionA small bead of mass m = 1 kg is free to move on a circular hoop. The circular hoop has centre at C and radius r = 1 m and it rotates about a fixed vertical axis. The coefficient of friction between bead and hoop is μ=0.5. The maximum angular speed of the hoop for which the bead does not have relative motion with respect to hoop, at the position shown in figure is : (Take g=10m/s2)
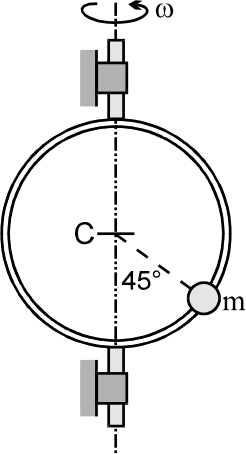
View SolutionA small bead of mass 'm' is threaded on a frictionless circulat wire of radius 'a' . The circule wire frame is rotated about its vertical diameter as shown. (assume acceleration due to grasvity is g) The angular speed required if the bead is to be made to move in a horizontal circle of radius (a sqrt(3))/(2) is :
View SolutionA thin insulating wire is stretched·along the diameter of an. insulated circular hoop of radius R. A small bead of mass m and charge-q is threaded onto the wire. Two small identical charges are tied to the hoop at points opposite to each other, so that the diameter passing through them is perpendicular to the thread as shown in figure. The bead is released at a point which.is located at a distance x0 from the centre of the hoop. Assume that x0<<R.
(a) What is the resultant force acting on the charged bead?
(b) Describe the motion of the bead after it is released X
(c) Use the assumption that xR<<1 to obtain an approximate equation of motion, and find the displacement and velocity of the bead as functions of time
(d) When will the velocity of the bead will bcome zero for the first time?

View SolutionTwo small spheres each of mass m are suspended from a common point by threads 0.5 m long. They are equally charged and repel each other to a distance of 0.28m. If =g10ms^(-2) , what is the charge on each sphere?
View SolutionA small bead of mass M slides on a smooth wire that is bent in a circle of radius R. It is released at the top of the circular part of the wire (point A in the figure) with a negligibly small velocity. Find the height H where the bead will reverse direction
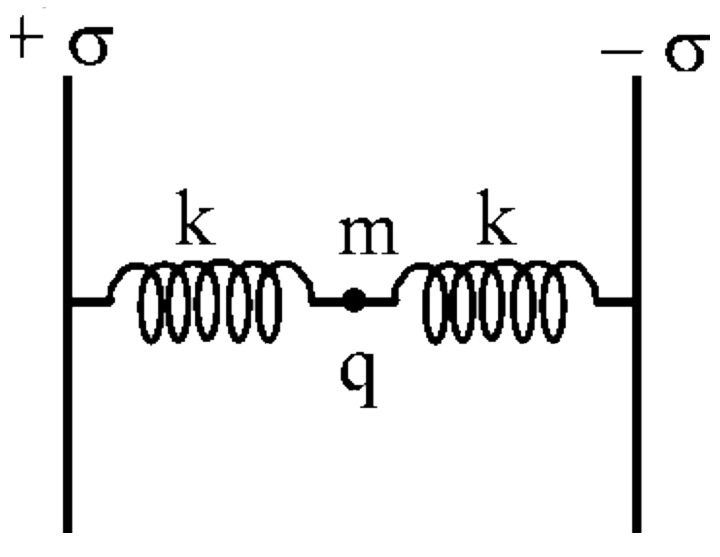
View Solutionपृष्ठीय आवेश घनत्व +σ और -σ वाली दो बड़ी विद्युतरोधी प्लेटें एक दूसरे से d दूरी पर रखी जाती हैं। द्रव्यमान m का एक छोटा परीक्षण आवेश q दो समरूप स्प्रिंगों से जुड़ा हुआ है, जैसा कि आकृति में दिखाया गया है। अब आवेश q, प्राकृतिक लंबाई में स्प्रिंगों के साथ विरामावस्था से छोड़ा जाता है, तो q : (गुरुत्व को नगण्य मान लीजिए)
View SolutionA wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
View Solution
