A stone is allowed to fall from the top of a tower 100m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25m/s. Calculate when and where the two stone will meet.
To solve the problem of when and where the two stones will meet, we can break it down into several steps.
Step 1: Understand the Problem
We have two stones:
1. Stone A is dropped from a height of 100 meters (initial velocity = 0 m/s).
2. Stone B is projected upwards from the ground with an initial velocity of 25 m/s.
Step 2: Define the Motion of Each Stone
- For Stone A (falling down):
- Initial height (h) = 100 m
- Initial velocity (u) = 0 m/s
- Acceleration (a) = g = 9.8 m/s² (approximately 10 m/s² can be used for simplicity)
Using the equation of motion:
s=ut+12at2
The distance fallen by Stone A after time t is:
sA=0⋅t+12gt2=12gt2
- For Stone B (moving up):
- Initial velocity (u) = 25 m/s
- Acceleration (a) = -g (since it is moving against gravity)
The distance traveled by Stone B after time t is:
sB=ut+12at2=25t−12gt2
Step 3: Set Up the Meeting Condition
At the time of meeting, the distance fallen by Stone A plus the distance traveled by Stone B should equal the height of the tower:
sA+sB=100
Substituting the expressions for sA and sB:
12gt2+(25t−12gt2)=100
This simplifies to:
25t=100
Step 4: Solve for Time t
From the equation 25t=100:
t=10025=4 seconds
Step 5: Calculate the Distance Where They Meet
Now, we can find the distance traveled by either stone in 4 seconds. We can use Stone B's equation:
sB=25t−12gt2
Substituting t=4 seconds and g≈10:
sB=25⋅4−12⋅10⋅(42)
sB=100−12⋅10⋅16
sB=100−80=20 meters
Conclusion
The two stones will meet after 4 seconds at a height of 20 meters above the ground.
Summary of Results
- Time of meeting: 4 seconds
- Height of meeting: 20 meters above the ground (or 80 meters below the top of the tower)
We have two stones:
1. Stone A is dropped from a height of 100 meters (initial velocity = 0 m/s).
2. Stone B is projected upwards from the ground with an initial velocity of 25 m/s.
- For Stone A (falling down):
- Initial height (h) = 100 m
- Initial velocity (u) = 0 m/s
- Acceleration (a) = g = 9.8 m/s² (approximately 10 m/s² can be used for simplicity)
Using the equation of motion:
s=ut+12at2
The distance fallen by Stone A after time t is:
sA=0⋅t+12gt2=12gt2
- Initial velocity (u) = 25 m/s
- Acceleration (a) = -g (since it is moving against gravity)
The distance traveled by Stone B after time t is:
sB=ut+12at2=25t−12gt2
At the time of meeting, the distance fallen by Stone A plus the distance traveled by Stone B should equal the height of the tower:
sA+sB=100
Substituting the expressions for sA and sB:
12gt2+(25t−12gt2)=100
This simplifies to:
25t=100
From the equation 25t=100:
t=10025=4 seconds
Now, we can find the distance traveled by either stone in 4 seconds. We can use Stone B's equation:
sB=25t−12gt2
Substituting t=4 seconds and g≈10:
sB=25⋅4−12⋅10⋅(42)
sB=100−12⋅10⋅16
sB=100−80=20 meters
The two stones will meet after 4 seconds at a height of 20 meters above the ground.
- Time of meeting: 4 seconds
- Height of meeting: 20 meters above the ground (or 80 meters below the top of the tower)
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - Short answer28videos
GRAVITATION
- BOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - Long answer7videos
GRAVITATION
- BOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - Model Test paper (1)36videos
GRAVITATION
- BOOK - PRADEEPCHAPTER - FORCES AND LAWS OF MOTIONEXERCISE - MOCK TEST36videos
FORCES AND LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - MOTIONEXERCISE - Mock test24videos
MOTION
Similar Questions

A stone is allowed to fall from the top of a tower 300 m height and at the same time another stone is projected vertically up from the ground with a velocity 100m/s. Find when and where the two stones meet?View SolutionA stone is dropped from the top of a tower 200 m high. At the same time, another stone is projected vertically upwards from the ground with a velocity of 40m/s. Calcuate when and where the two stones will mest.
View Solution
Knowledge Check
- Question 1 - Select One
A stone is dropped from the top of a 400m high tower. At the same time another stone is projected vertically upwards from the ground with a speed of 50m/s. The two stones will cross each other after a time
A2 sB4 sC6 sD8 s - Question 2 - Select One
One stone is dropped from a tower from rest and simultaneously another stone is projected vertically upwards from the tower with some initial velocity. The graph of distance (s) between the two stones varies with time (t) as (before either stone hits the ground).
A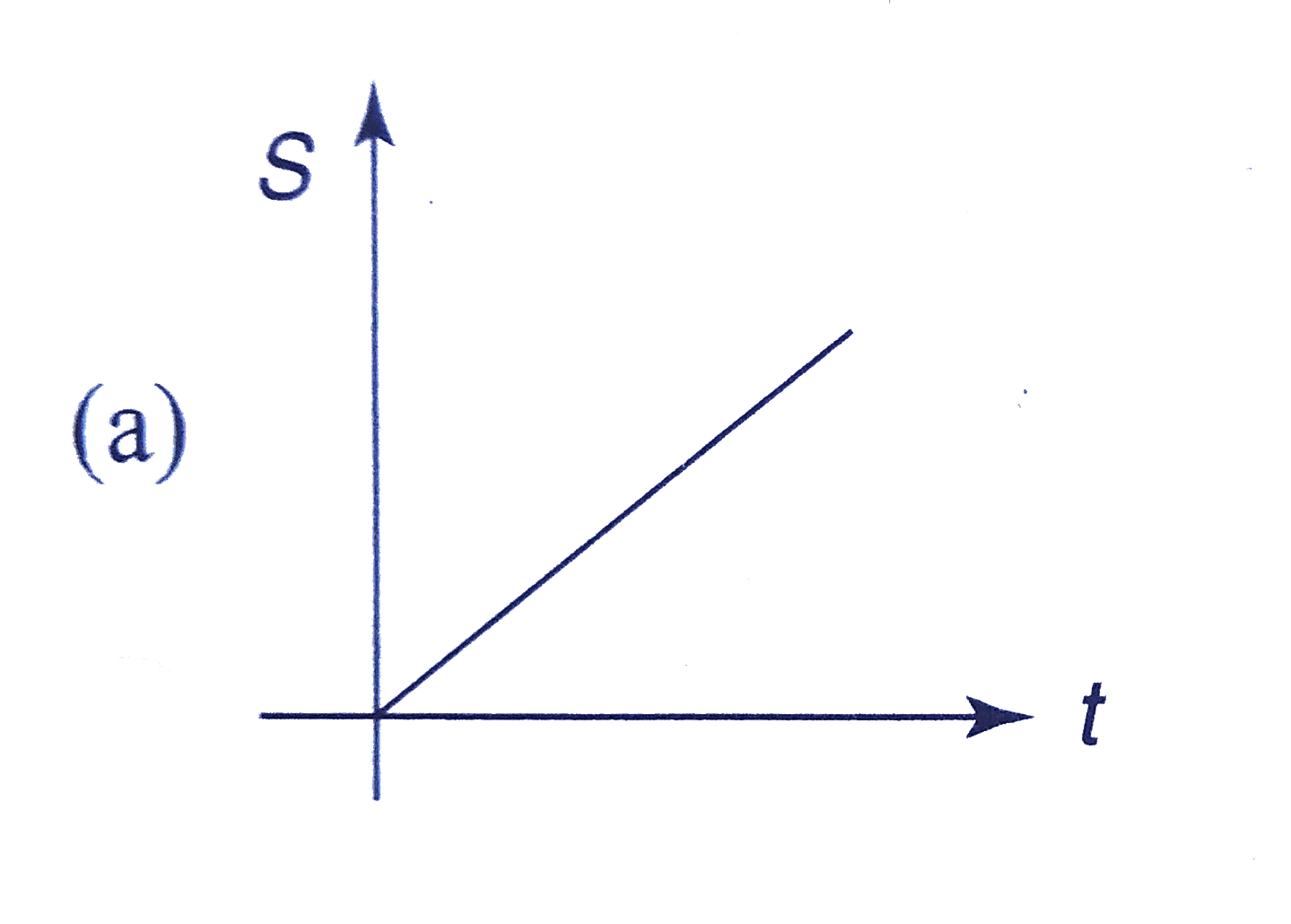 .B
.B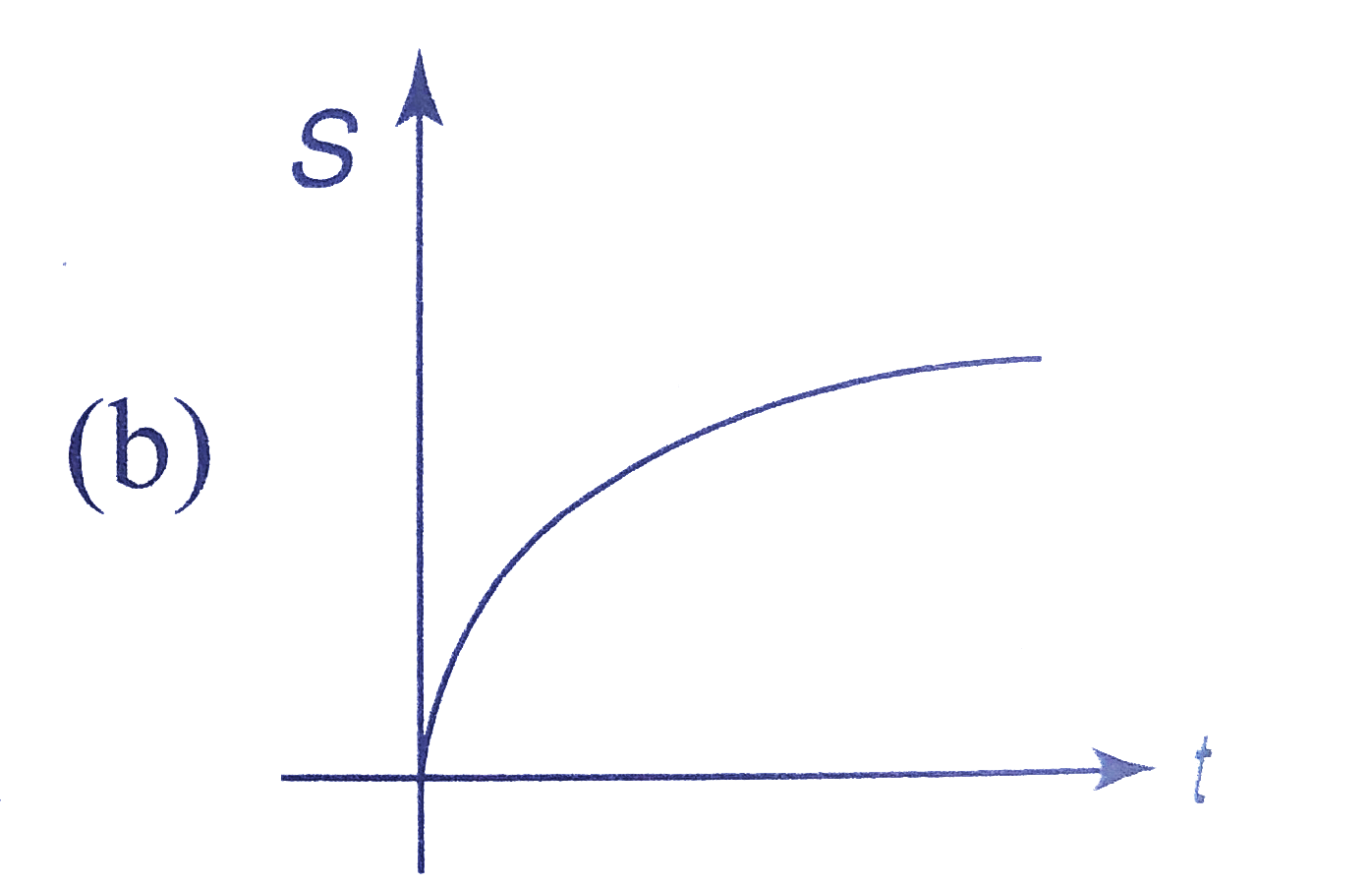 .C
.C .D
.D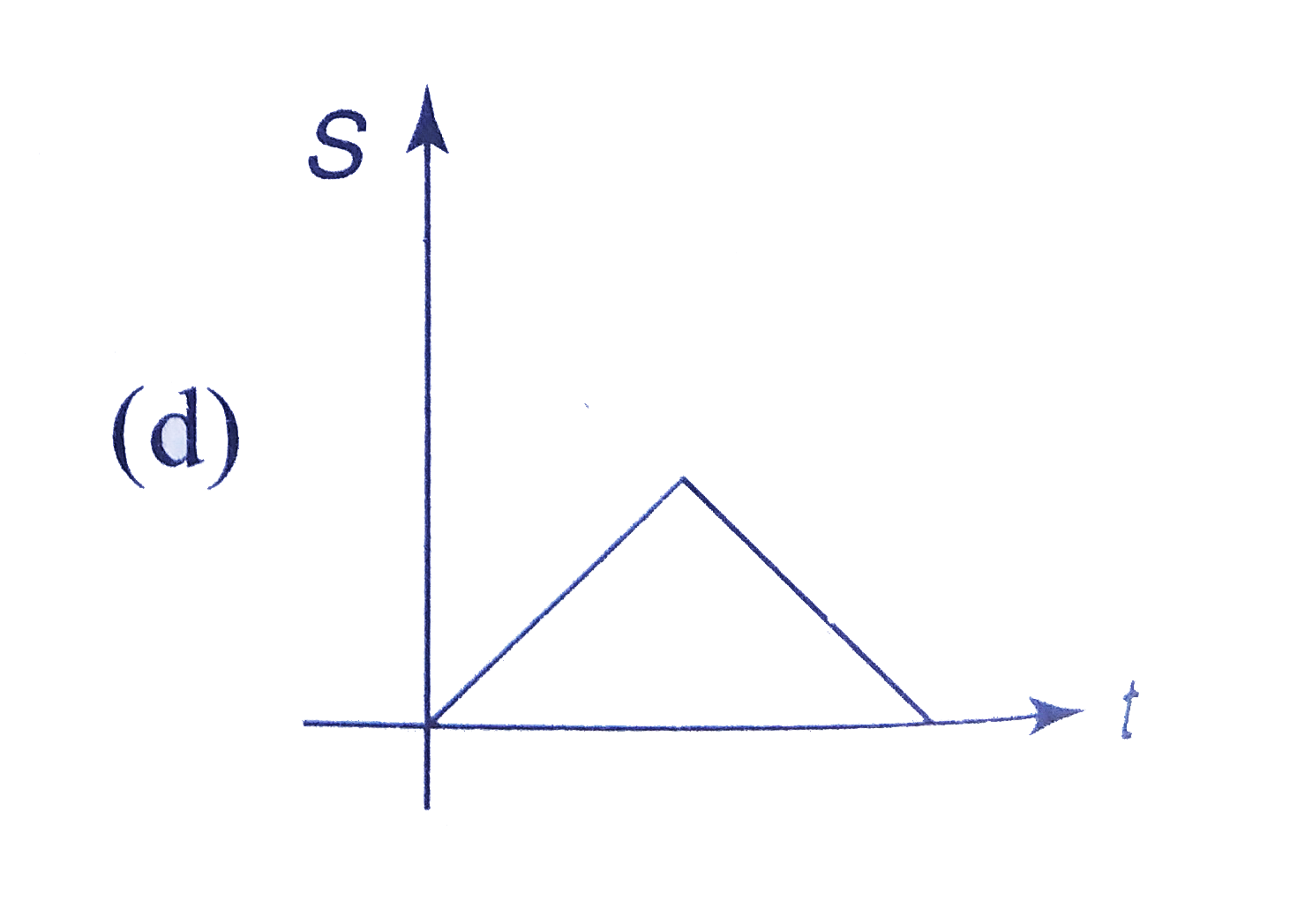 .
.
Form the top of a tower 100m in height a ball is dropped and at the same time another ball is projected vertically upwards from the ground with a velcoity of 25ms−1. Find when and where the two balls will meet.
View SolutionFrom the top of a tower 100 m in height a ball is dropped and at the same time another ball is projected vertically upwards from the ground with a velocity of 25 m/s. Find when and where the two balls will meet? (g=9.8m/s)
View SolutionA ball A is dropped from the top of a tower 500m high and at the same instant another ball b is projected upwards with the velocity of 100m/s. after how much time and where the two balls will meet?
View SolutionA stone is dropped from a height of 100m .At the same instant another stone is projected vertically upwards with velocity of 50ms^(-1) .If g=10ms^(-2) ,the height from the ground at which the 2 stones meet is
View SolutionA stone is released from the top of a tower of height 1960 m. calculate the time taken by the stone to hit the ground.
View SolutionA stone is dropped form 100 m high cliff. Another stone is thrown upward from ground with a velocity 10m/s. At what time both the stones will meet each other ?
View Solution
