A stone is dropped at t=0. A second stone, will twice the mass of the first, is dropped from the same point at t=100ms.
(a) How far below the release point is the centre of mass of the two stones at t=300ms?(Neither stone has yet reached at groung).
(b) How fast is the centre of the mass of the two-stone system moving at that time?
The correct Answer is:A, B, C
To solve the problem, we will break it down into two parts as stated in the question.
Part (a): Finding the distance of the center of mass below the release point at t=300ms
1. Identify the masses and times:
- Let the mass of the first stone (Stone A) be m.
- The mass of the second stone (Stone B) is 2m.
- Stone A is dropped at t=0ms.
- Stone B is dropped at t=100ms.
2. Calculate the time each stone has been falling at t=300ms:
- For Stone A:
t1=300ms−0ms=300ms=0.3s
- For Stone B:
t2=300ms−100ms=200ms=0.2s
3. Calculate the distance fallen by each stone:
- Using the formula for distance fallen under gravity:
d=12gt2
- For Stone A:
d1=12⋅10m/s2⋅(0.3s)2=12⋅10⋅0.09=0.45m
- For Stone B:
d2=12⋅10m/s2⋅(0.2s)2=12⋅10⋅0.04=0.2m
4. Calculate the center of mass (CM) position:
- The formula for the center of mass dcm of two masses is:
dcm=m1d1+m2d2m1+m2
- Substituting the values:
dcm=m⋅0.45+2m⋅0.2m+2m=0.45m+0.4m3m=0.85m3m=0.853≈0.2833m=28.3cm
Part (b): Finding the velocity of the center of mass at t=300ms
1. Calculate the velocity of each stone:
- The velocity of an object falling under gravity is given by:
v=gt
- For Stone A:
v1=g⋅t1=10m/s2⋅0.3s=3m/s
- For Stone B:
v2=g⋅t2=10m/s2⋅0.2s=2m/s
2. Calculate the velocity of the center of mass:
- Using the formula for the velocity of the center of mass:
vcm=m1v1+m2v2m1+m2
- Substituting the values:
vcm=m⋅3+2m⋅2m+2m=3m+4m3m=7m3m=73≈2.33m/s
Final Answers:
(a) The center of mass is approximately 28.3cm below the release point.
(b) The velocity of the center of mass is approximately 2.33m/s.
- Let the mass of the first stone (Stone A) be m.
- The mass of the second stone (Stone B) is 2m.
- Stone A is dropped at t=0ms.
- Stone B is dropped at t=100ms.
- For Stone A:
t1=300ms−0ms=300ms=0.3s
- For Stone B:
t2=300ms−100ms=200ms=0.2s
- Using the formula for distance fallen under gravity:
d=12gt2
- For Stone A:
d1=12⋅10m/s2⋅(0.3s)2=12⋅10⋅0.09=0.45m
- For Stone B:
d2=12⋅10m/s2⋅(0.2s)2=12⋅10⋅0.04=0.2m
- The formula for the center of mass dcm of two masses is:
dcm=m1d1+m2d2m1+m2
- Substituting the values:
dcm=m⋅0.45+2m⋅0.2m+2m=0.45m+0.4m3m=0.85m3m=0.853≈0.2833m=28.3cm
- The velocity of an object falling under gravity is given by:
v=gt
- For Stone A:
v1=g⋅t1=10m/s2⋅0.3s=3m/s
- For Stone B:
v2=g⋅t2=10m/s2⋅0.2s=2m/s
- Using the formula for the velocity of the center of mass:
vcm=m1v1+m2v2m1+m2
- Substituting the values:
vcm=m⋅3+2m⋅2m+2m=3m+4m3m=7m3m=73≈2.33m/s
(a) The center of mass is approximately 28.3cm below the release point.
(b) The velocity of the center of mass is approximately 2.33m/s.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.3
7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.4
4 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.1
13 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
Consider a system of two identical masses. One is dropped from a height and another is thrown from ground with speed U. The acceleration of centre of mass of the system at time t is
View SolutionA stone is dropped off the edge of a cliff. The height (h metres) of the cliff is proportional to the square of the time (t seconds) taken by the stone to reach the ground.
Write down a relationship between h and t, using k as the constant of variation.
View Solution
Knowledge Check
A stone is dropped from a building, and 2 seconds later another stone is dropped. How far apart are the two stones by the time the first one has reached a speed of 30 m/s?
A80mB60mC20mD40mOne stone is dropped from a tower from rest and simultaneously another stone is projected vertically upwards from the tower with some initial velocity. The graph of distance (s) between the two stones varies with time (t) as (before either stone hits the ground).
A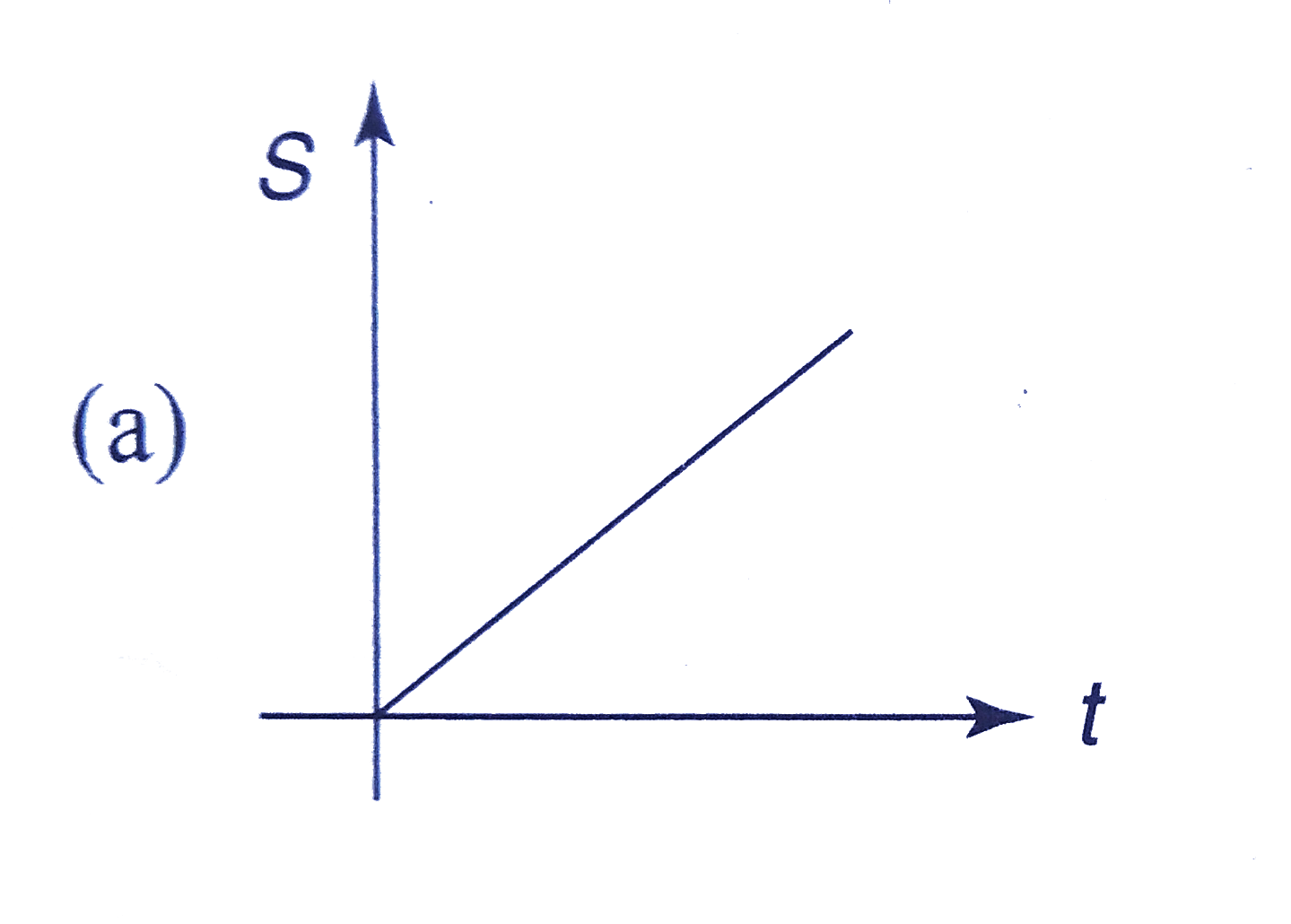 .B
.B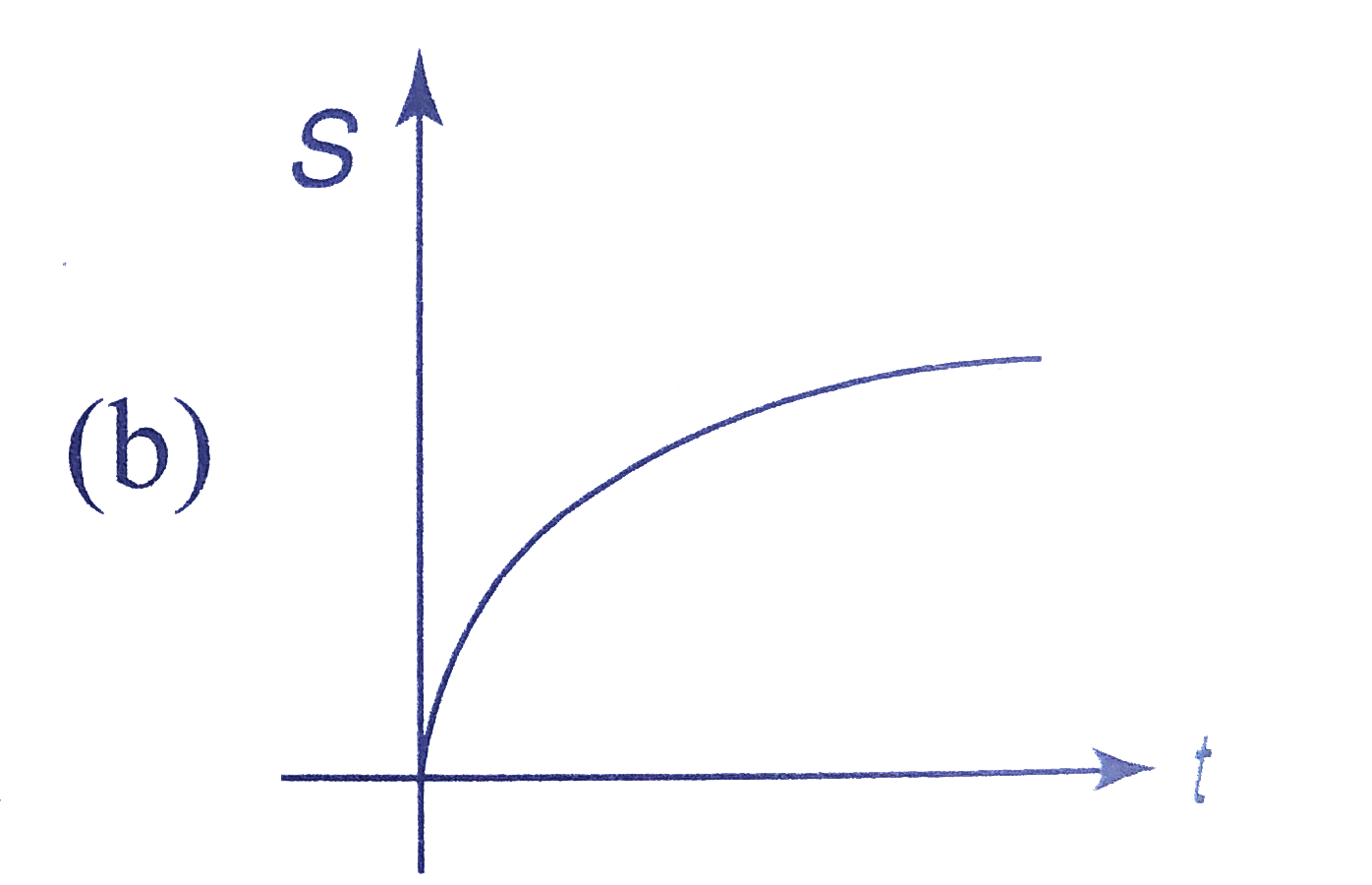 .C
.C .D
.D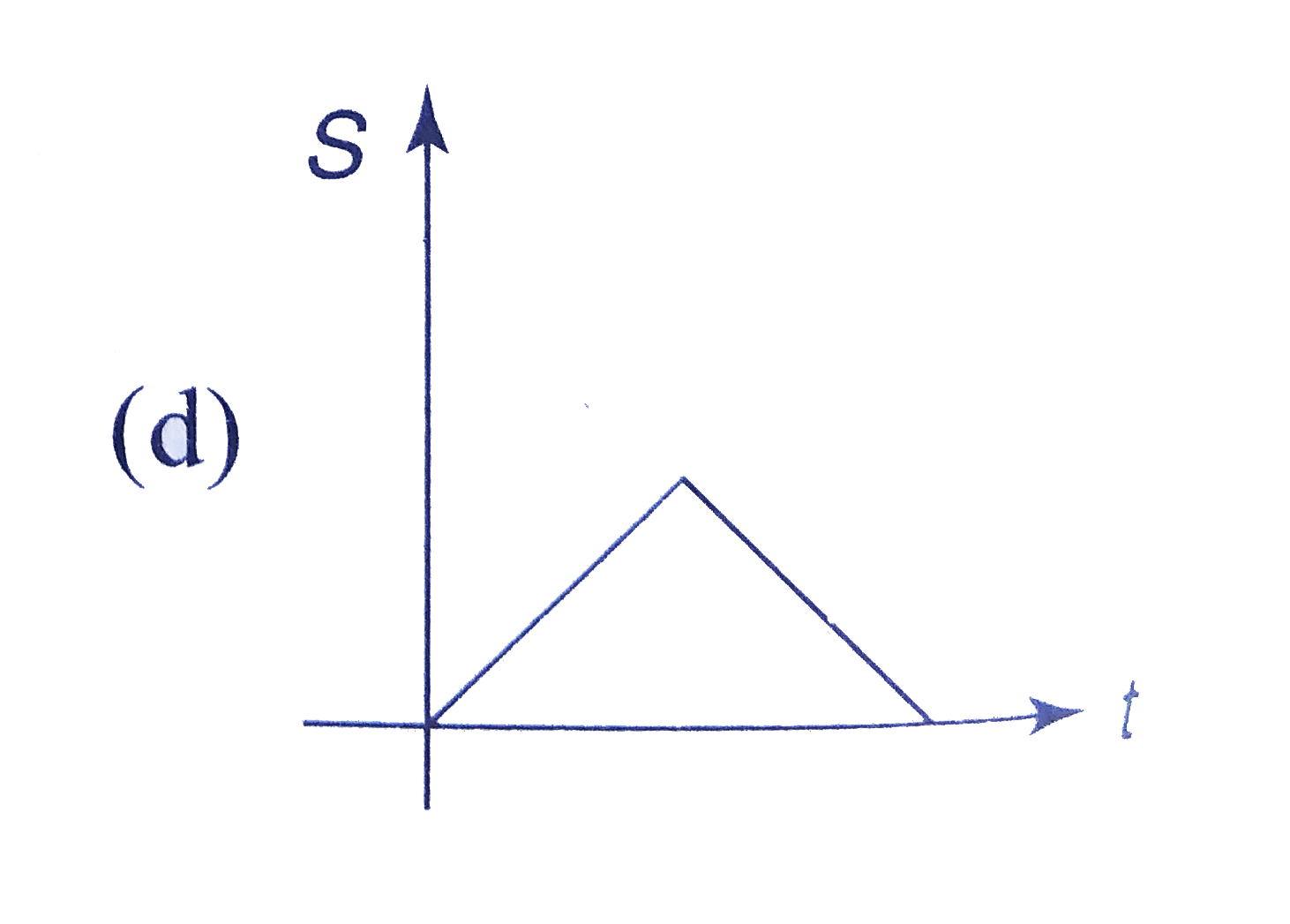 .
.Assertion : A stone and a feather dropped from the same height do not reach the ground at the same time.
Reason : Acceleration due to gravity is dependent on the mass of the object.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
A stone is dropped from the top of tall tower and one second later another stone is dropped from a balcany 20 m below the top . If both the stones reach the ground at the same instant , determine the height of the tower .take g=10ms−2
View SolutionA stone is dropped into a river from a bridge 53.6 m above the water. Another stone is thrown vertically down 1.00 s after the first is dropped. The stones strike the water at the same time. (a) What is the initial speed of the second stone ? (b) Plot velocity versus time on a graph for each stone, taking zero time as the instant the first stone is released .
View SolutionA stone of mass 500g is dropped from the top of a tower of 100m height. Simultaneously another stone of mass 1 kg is thrown horizontally with a speed of 10ms−1 from same point. The height of the centre of mass of the above two stone system after 3 sec is (g=10ms−2)
View SolutionA stone of mass 500g is dropped from the top of a tower of 100m height. Simultaneously another stone of mass 1 kg is thrown horizontally with a speed of 10ms−1 from same point. The height of the centre of mass of the above two stone system after 3 sec is (g=10ms−2)
View SolutionTwo stones of different masses are dropped simultaneously from the top of a building
View Solution
