Consider a system of two identical masses. One is dropped from a height and another is thrown from ground with speed U. The acceleration of centre of mass of the system at time t is
g2
g
2g
Zero
To solve the problem, we need to analyze the motion of both masses and then find the acceleration of the center of mass of the system.
1. Identify the Masses and Their Initial Conditions:
- Let the mass of each object be m.
- One mass (let's call it m1) is dropped from a height h (initial velocity u1=0).
- The other mass (let's call it m2) is thrown upwards from the ground with an initial speed U (initial velocity u2=U).
2. Determine the Acceleration of Each Mass:
- The acceleration due to gravity acts on both masses. Therefore:
- The acceleration of m1 (the dropped mass) is a1=g (downward).
- The acceleration of m2 (the thrown mass) is a2=−g (upward, since it is thrown upwards).
3. Calculate the Position of Each Mass at Time t:
- For m1 (dropped from height h):
y1=h−12gt2
- For m2 (thrown upwards):
y2=Ut−12gt2
4. Calculate the Center of Mass (CM) of the System:
- The position of the center of mass YCM is given by:
YCM=m1y1+m2y2m1+m2
- Since m1=m2=m:
YCM=m(h−12gt2)+m(Ut−12gt2)2m
YCM=h+Ut−gt22
5. Differentiate to Find the Velocity of the Center of Mass:
- To find the velocity VCM, differentiate YCM with respect to time t:
VCM=ddt(h+Ut−gt22)=U−gt2
6. Differentiate Again to Find the Acceleration of the Center of Mass:
- To find the acceleration ACM, differentiate VCM with respect to time t:
ACM=ddt(U−gt2)=−g2
7. Conclusion:
- The acceleration of the center of mass of the system is −g (downward).
Final Answer:
The acceleration of the center of mass of the system at time t is −g (downward).
- Let the mass of each object be m.
- One mass (let's call it m1) is dropped from a height h (initial velocity u1=0).
- The other mass (let's call it m2) is thrown upwards from the ground with an initial speed U (initial velocity u2=U).
- The acceleration due to gravity acts on both masses. Therefore:
- The acceleration of m1 (the dropped mass) is a1=g (downward).
- The acceleration of m2 (the thrown mass) is a2=−g (upward, since it is thrown upwards).
- For m1 (dropped from height h):
y1=h−12gt2
- For m2 (thrown upwards):
y2=Ut−12gt2
- The position of the center of mass YCM is given by:
YCM=m1y1+m2y2m1+m2
- Since m1=m2=m:
YCM=m(h−12gt2)+m(Ut−12gt2)2m
YCM=h+Ut−gt22
- To find the velocity VCM, differentiate YCM with respect to time t:
VCM=ddt(h+Ut−gt22)=U−gt2
- To find the acceleration ACM, differentiate VCM with respect to time t:
ACM=ddt(U−gt2)=−g2
- The acceleration of the center of mass of the system is −g (downward).
The acceleration of the center of mass of the system at time t is −g (downward).
Topper's Solved these Questions
Similar Questions
Knowledge Check
The magnitude of acceleration of centre of mass of the system is
 A4m/sB10ms2C5ms2D2√2ms2
A4m/sB10ms2C5ms2D2√2ms2If the system is released, then the acceleration of the centre of mass of the system is :
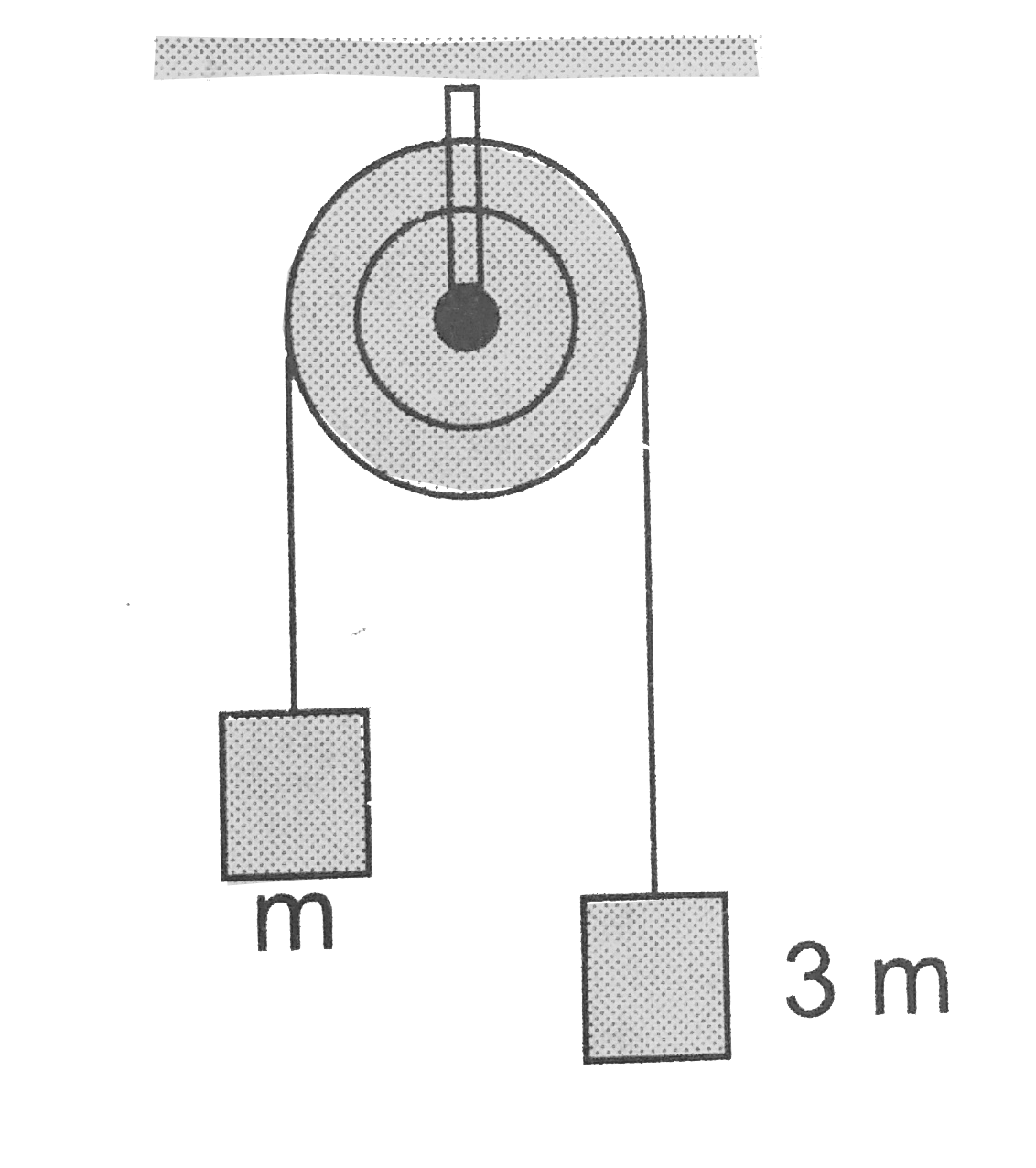 .Ag4Bg2CgD2 g
.Ag4Bg2CgD2 gThe centre of mass of two particles system lies
Aat the midpoint on the line joining the two particles.Bat one end of line joining the two particlesCon the line perpendicular to the line joining two particlesDon the line joining the two particles
If the system is released, then the acceleration of the centre of mass of the system :
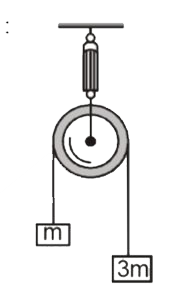
View SolutionA body is thrown from a height h with speed, u it hits the ground with speed v
View SolutionConsider a system of two identical particles. One of the particle is at rest and other has an acceleration →a. The centre of mass has an acceleration
View SolutionA stone is dropped from a height h. Simultaneously, another stone is thrown up from the ground which reaches a height 4 h. The two stones cross each other after time
View SolutionConsider a system of two identical particles. One of the particls is at rest and the other has an acceleration.The centre of mass has an acceleration vaca The centre of mass has an acceleration.
View Solution
