A straight wire carrying a current 10A is bent into a semicircular arc of radius 5cm. The magnitude of magnetic field at the center is
8A
4A
2A
1A
The correct Answer is:A
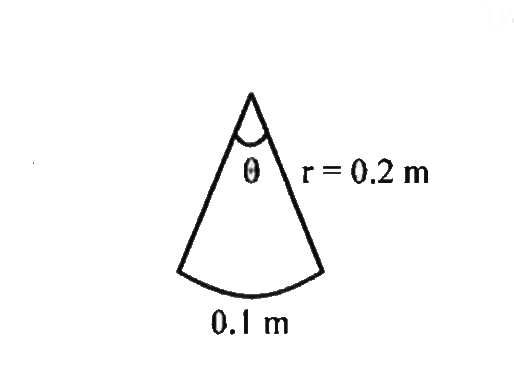
θ=arcradius=0.10.2=12 radian
∴ The dield (B) at the centre of a circular coil corresponds to 2π radian s.
∴For12 radian, the field will be B'B2×2π=B4π
Let I be teh current to produce the field,
B'=2×10−6T
∴B'=14π[μ04π2πIr]
∴2×10−6=14π×10−7×2πI0.2=10−7I2×0.2
∴I=2×2×0.2×10−610−7=8A
Note: The magnetic field dut to an are substending an angle θ at the centre is (θ2πB).
In this coseθ=12 raian and B'=B4π.
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - MCQ (GRAPHICAL MCQS)2videos
MAGNETIC EFFECT OF ELECTRIC CURRENT
- BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - TEST YOUR GRASP10videos
MAGNETIC EFFECT OF ELECTRIC CURRENT
- BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - MCQ (STANDARD LEVEL)46videos
MAGNETIC EFFECT OF ELECTRIC CURRENT
- BOOK - MARVEL PUBLICATIONCHAPTER - FRICTIONAL IN SOLIDS AND LIQUIDS EXERCISE - TEST YOUR GRASP10videos
FRICTIONAL IN SOLIDS AND LIQUIDS
- BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETISMEXERCISE - TEST YOUR GRASP10videos
MAGNETISM
Similar Questions
A straight wire carrying a current of 13 A is bent into a semi-circular arc of radius 2 cm as shown in figure. The magnetic field is 1.5×10−4T at the centre of arc, then the magnetic field due to straight segment is
 View Solution
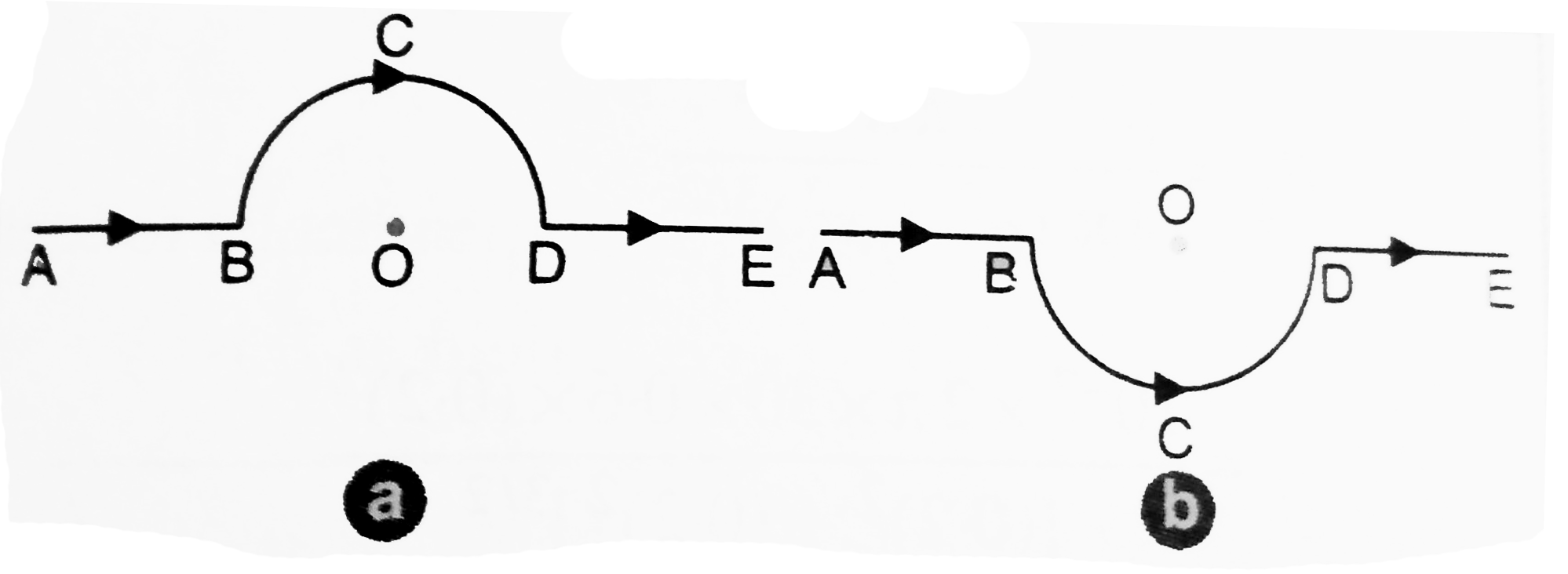
View SolutionA straight wire carrying a current of 12A is bent into a semicircular arc of radius 2⋅0cm as shown in figure. Consider the magnetic field →B at the centre of arc.
(a) What is the magnetic field due to the staight segments?
(b) In what way the contribution to →B from the semicircle differs from that of a circular loop and in what way does it resemble?
(c) Would your answer be different if the wire were bent into a semicircle arc of the same radius but in the opposite way as shown in figure
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A wire of length L carrying a current I is bent into a circle. The magnitude of the magnetic field at the centre of the circle is
Aπμ0ILBμ0I2LC2πμ0ILDμ0I2πL - Question 2 - Select One
A wire of length L carrying a current I is bent into a circle. The magnitude of the magneitc field at the centre of the circle is
Aπμ0ILBμ0I2LC2πμ0ILDμ0I2πL - Question 3 - Select One or More
A long straight conductor carrying a current i is bent to form an almost complete circular loop of radius r on it. The magnetic field at the centre of the loop
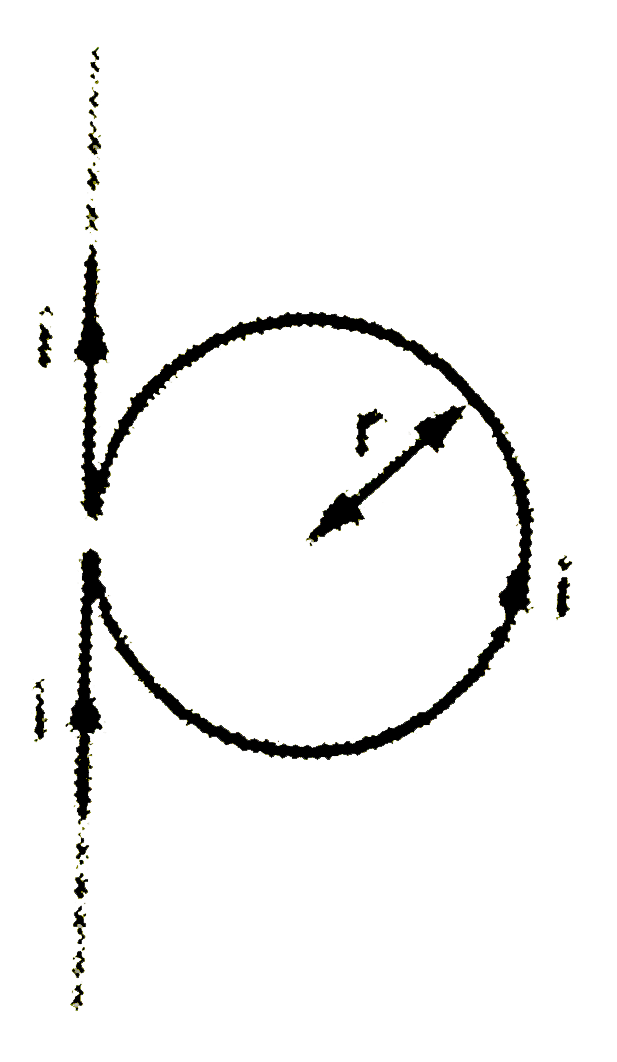 Ais directed into the paperBis directed out of the paperChas magnitude μ0i2r(1−1π)Dhas magnitude μ(0)i2r(1+1π)
Ais directed into the paperBis directed out of the paperChas magnitude μ0i2r(1−1π)Dhas magnitude μ(0)i2r(1+1π)
A straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the fig. Find the magnitude and direction of the magnetic field at the centre of the arc.
 View Solution
View SolutionA thick straight copper wire, carrying a current of 10 A is bent into a semicircular arc of radius 7.0 cm as a shown in Fig (a). (i) State the direction and calculate the magnitude of magnetic field at the centre of arc. (ii) How would your answer change if the same wire were bent into a semicircular arc of the same radius but in opposite way as shown in Fig. (b)?
 View Solution
View Solution(a) Derive the expression for the magnetic field due to a current carrying coil of radius r at a distance x from the centre along the X-axis.
(b) A straight wire carrying a current of 5 A is bent into a semicular arc of radius 2 cm as shown in the fig. FInd th magnitude and direction of the magnetic field at the centre of the arc.
 View Solution
View SolutionA straight wire carrying a current of 12 A is bent into a semi-circular are of radius of2.0 cm as shown in the adjoining figure (a). Consider the magnetic field B at the centre of the arc. Would your answer be different if the wire were bent into a semi-circular arc of the same radius but in the opposite way a shown in figure (b)?
 View Solution
View SolutionA straight wire carrying a current is turned into a circular loop if the magnitude of magnetic moment associated with it is M then the length of the wire will be
View Solution

