A straight wire carrying a current of 13 A is bent into a semi-circular arc of radius 2 cm as shown in figure. The magnetic field is 1.5×10−4T at the centre of arc, then the magnetic field due to straight segment is

1.5×10−4T
2.5×10−4T
zero
3×10−4T
The correct Answer is:C
Since dl and r for each element of the straight segments are parallel. Therefore
→dl×→r=0
Hence, B is also zero.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTIPSCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Ampere'S Circuit Law
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTIPSCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - The Solenoid And The Toroid
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTIPSCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Magnetic Field Due To A Current Element, Biot-Savart Law
4 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTIPSCHAPTER - MAGNETISM AND MATTER EXERCISE - Assertion And Reason
15 Videos
- NUCLEIBOOK - NCERT FINGERTIPSCHAPTER - NUCLEIEXERCISE - Assertion And Reason
15 Videos
Similar Questions
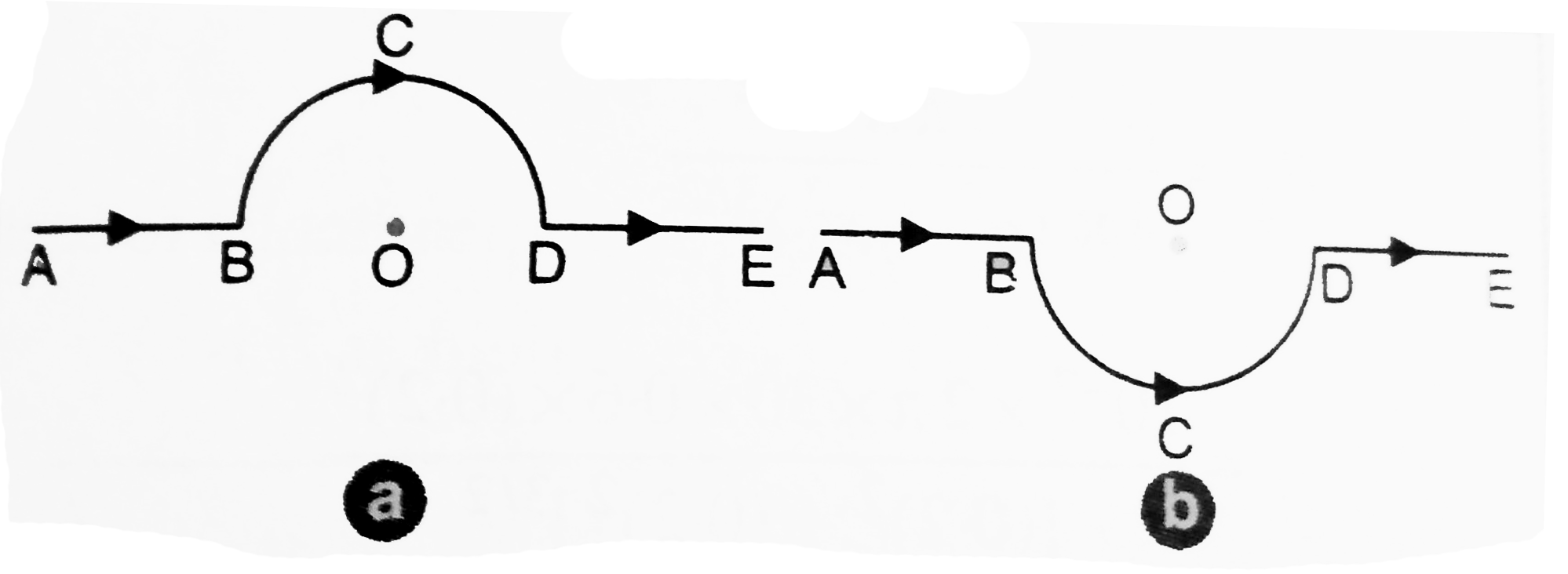
A straight wire carrying a current of 12A is bent into a semicircular arc of radius 2⋅0cm as shown in figure. Consider the magnetic field →B at the centre of arc.
(a) What is the magnetic field due to the staight segments?
(b) In what way the contribution to →B from the semicircle differs from that of a circular loop and in what way does it resemble?
(c) Would your answer be different if the wire were bent into a semicircle arc of the same radius but in the opposite way as shown in figure
View SolutionA straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the fig. Find the magnitude and direction of the magnetic field at the centre of the arc.

View Solution
Knowledge Check
A straight wire carrying a current 10A is bent into a semicircular arc of radius 5cm. The magnitude of magnetic field at the center is
A1.5×10−5TB3.14×10−5TC6.28×10−5TD19.6×10−5TA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
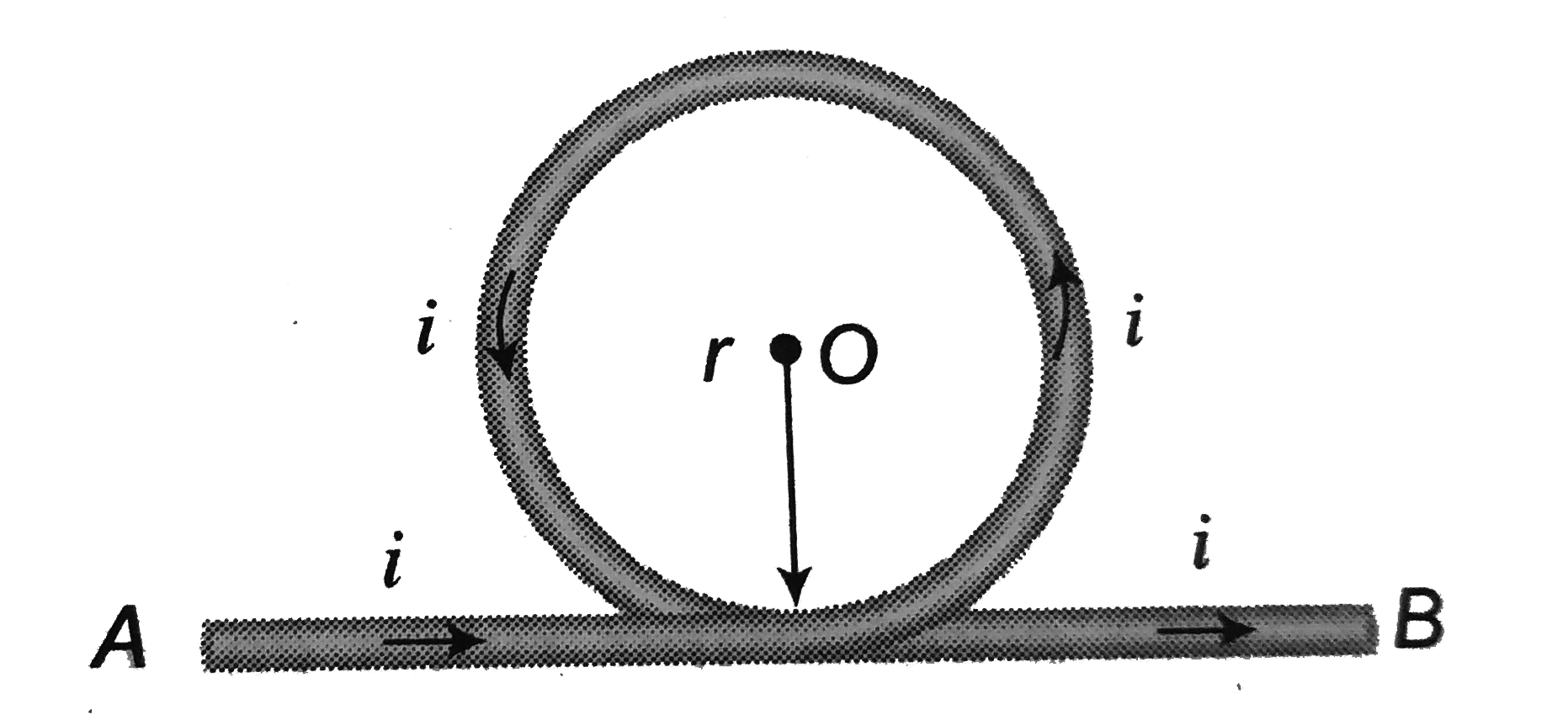 Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
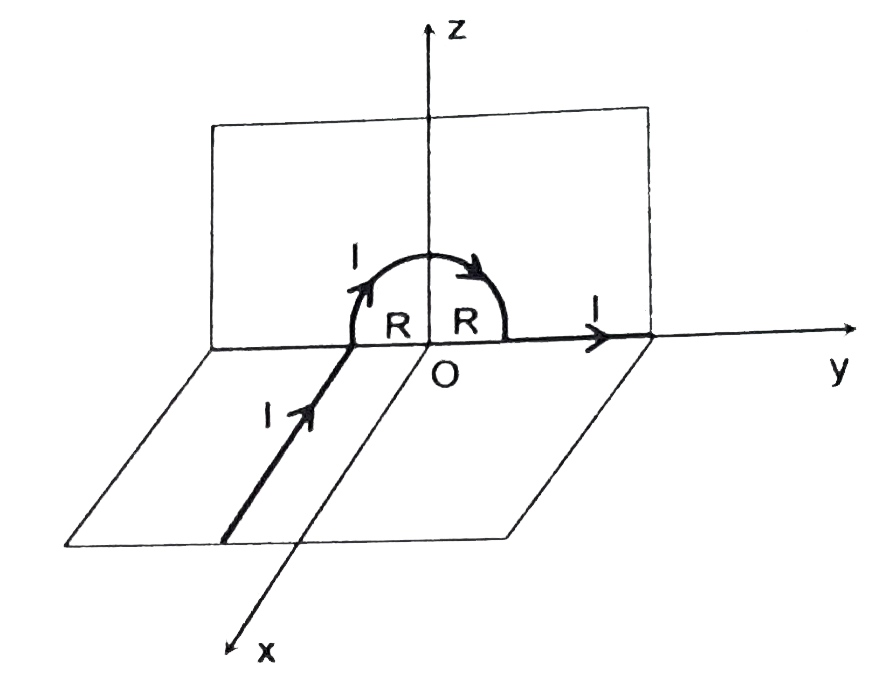 Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
A straight wire carrying a current of 12 A is bent into a semi-circular are of radius of2.0 cm as shown in the adjoining figure (a). Consider the magnetic field B at the centre of the arc. Would your answer be different if the wire were bent into a semi-circular arc of the same radius but in the opposite way a shown in figure (b)?

View SolutionA thick straight copper wire, carrying a current of 10 A is bent into a semicircular arc of radius 7.0 cm as a shown in Fig (a). (i) State the direction and calculate the magnitude of magnetic field at the centre of arc. (ii) How would your answer change if the same wire were bent into a semicircular arc of the same radius but in opposite way as shown in Fig. (b)?

View Solution(a) Derive the expression for the magnetic field due to a current carrying coil of radius r at a distance x from the centre along the X-axis.
(b) A straight wire carrying a current of 5 A is bent into a semicular arc of radius 2 cm as shown in the fig. FInd th magnitude and direction of the magnetic field at the centre of the arc.

View SolutionA piece of wire carrying a current of 6.00 A is bent in the form of a circular arc of radius 10.0 cm, and it subtends an angle of 120∘ at the centre. Find the magnetic field B due to this piece of wire at the centre.
View SolutionA long straight conductor carrying a current i is bent to form an almost complete circular loop of radius r on it. The magnetic field at the centre of the loop
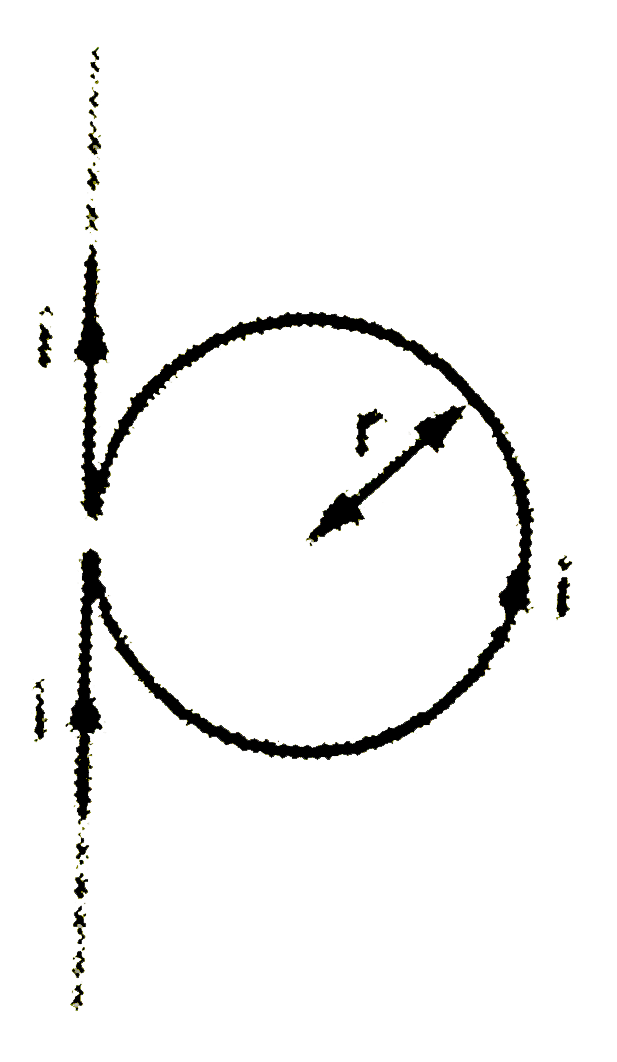
View Solution
