A straight wire is first bent into a circle of radius 'r' and then into a square of side 'a' each of 1 turn. If the currents flowing through them are in the ratio 2:3, find the ratio between their effective magnetic moments?
To solve the problem, we need to find the ratio of the effective magnetic moments of a circular loop and a square loop formed from the same length of wire. We will use the formula for the magnetic moment, which is given by:
M=I×A
where M is the magnetic moment, I is the current, and A is the area enclosed by the loop.
Step 1: Define the lengths and areas
1. Let the total length of the wire be L.
2. For the circular loop of radius r:
- The circumference (length of wire used) is L=2πr.
- The area A1 of the circle is given by:
A1=πr2
3. For the square loop of side a:
- The perimeter (length of wire used) is L=4a.
- The area A2 of the square is given by:
A2=a2
Step 2: Express r and a in terms of L
From the equations for the circumference and perimeter:
- For the circle:
r=L2π
- For the square:
a=L4
Step 3: Calculate the areas in terms of L
1. Substitute r into the area of the circle:
A1=π(L2π)2=πL24π2=L24π
2. Substitute a into the area of the square:
A2=(L4)2=L216
Step 4: Calculate the magnetic moments
1. Let the currents through the circular loop and square loop be I1 and I2, respectively. Given that the currents are in the ratio I1I2=23:
I1=2kandI2=3kfor some constant k
2. The magnetic moments are:
- For the circular loop:
M1=I1×A1=(2k)×(L24π)=2kL24π=kL22π
- For the square loop:
M2=I2×A2=(3k)×(L216)=3kL216
Step 5: Find the ratio of the magnetic moments
Now, we can find the ratio of the magnetic moments M1M2:
M1M2=kL22π3kL216=162π⋅3=166π=83π
Final Answer
Thus, the ratio of the effective magnetic moments of the circular loop to the square loop is:
M1M2=83π
1. Let the total length of the wire be L.
2. For the circular loop of radius r:
- The circumference (length of wire used) is L=2πr.
- The area A1 of the circle is given by:
A1=πr2
- The perimeter (length of wire used) is L=4a.
- The area A2 of the square is given by:
A2=a2
From the equations for the circumference and perimeter:
- For the circle:
r=L2π
a=L4
1. Substitute r into the area of the circle:
A1=π(L2π)2=πL24π2=L24π
A2=(L4)2=L216
1. Let the currents through the circular loop and square loop be I1 and I2, respectively. Given that the currents are in the ratio I1I2=23:
I1=2kandI2=3kfor some constant k
- For the circular loop:
M1=I1×A1=(2k)×(L24π)=2kL24π=kL22π
M2=I2×A2=(3k)×(L216)=3kL216
Now, we can find the ratio of the magnetic moments M1M2:
M1M2=kL22π3kL216=162π⋅3=166π=83π
Thus, the ratio of the effective magnetic moments of the circular loop to the square loop is:
M1M2=83π
Topper's Solved these Questions
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
13 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - PROBLEMS (LEVEL -I)
40 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
5 Videos
Similar Questions
A straight wire is first bent into a circle of radius 'r' and then into a square of side 'x' each of oneturn. If currents flowing through them are in the ratio 4 : 5, the ratio of their effective magnetic moments is
View SolutionA wire is bent in the form of a circular arc of radius r with a straight portion AB. If the current in the wire is i, then the magnetic induction at point O is
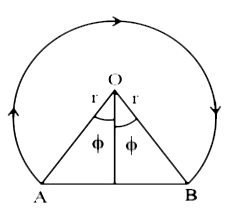
View SolutionTwo identical wires AandB , each of length 'l', carry the same current I. Wire A is bent into a circle of radius RandwireB is bent to form a square of side 'a' . If BAandBB are the values of magnetic field at the centres of the circle and square respectively , then the ratio BABB is :
View SolutionTwo identical wires AandB , each of length 'l', carry the same current I. Wire A is bent into a circle of radius RandwireB is bent to form a square of side 'a' . If BAandBB are the values of magnetic field at the centres of the circle and square respectively , then the ratio BABB is :
View SolutionA circular loop and a square loop are formed from the same wire and the same current is passed through them . Find the ratio of their dipole moments.
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
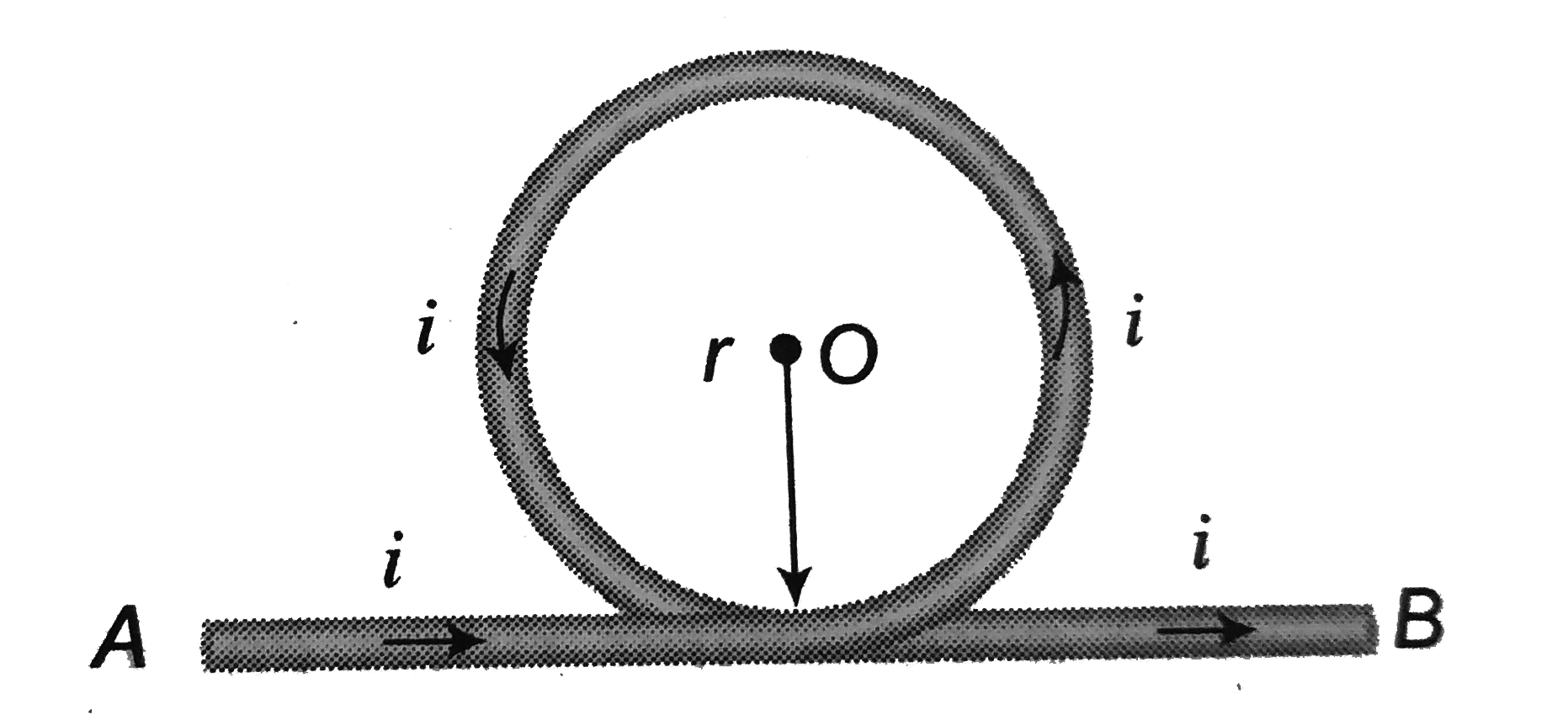
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

View SolutionA current of I amperes is flowing through each of the bent wires as shown. Find the magnitude of magnetic field at O.
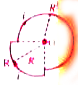
View SolutionAn electron moves with a constant speed v along a circle of radius r.(a) find the equivalent current through a point on its path.(b) Find the magnetic moment of the circulating electron.(c ) Find the ratio of the magnetic moment to the angular momentum of the electron.
View SolutionTwo wires of the same length are shaped into a square and a circle. If they carry same current, ratio of the magnetic moment is
View Solution
