A straight wire is first bent into a circle of radius 'r' and then into a square of side 'x' each of oneturn. If currents flowing through them are in the ratio 4 : 5, the ratio of their effective magnetic moments is
π8
125π
165π
85π
The correct Answer is:C
To solve the problem, we need to find the ratio of the effective magnetic moments of a wire bent into a circle and a square, given the currents flowing through them in the ratio of 4:5.
1. Determine the Length of the Wire:
Let the length of the wire be l.
2. Wire Bent into a Circle:
- The circumference of the circle is given by:
l=2πr
- From this, we can express the radius r in terms of l:
r=l2π
- The area A1 of the circle is:
A1=πr2=π(l2π)2=l24π
3. Wire Bent into a Square:
- The perimeter of the square is given by:
4x=l⟹x=l4
- The area A2 of the square is:
A2=x2=(l4)2=l216
4. Magnetic Moment Calculation:
- The magnetic moment M for a loop is given by:
M=I⋅A
- For the circle, the magnetic moment M1 is:
M1=I1⋅A1=I1⋅l24π
- For the square, the magnetic moment M2 is:
M2=I2⋅A2=I2⋅l216
5. Current Ratio:
- Given that the currents are in the ratio:
I1I2=45
- We can express I1 in terms of I2:
I1=45I2
6. Ratio of Magnetic Moments:
- Now substituting I1 into the expression for M1:
M1=(45I2)⋅l24π=4I2l220π=I2l25π
- Now we can find the ratio of the magnetic moments:
M1M2=I2l25πI2⋅l216=15π⋅16l2=165π
7. Final Result:
- Therefore, the ratio of the effective magnetic moments is:
M1M2=165π
Conclusion:
The ratio of their effective magnetic moments is 165π.
Let the length of the wire be l.
- The circumference of the circle is given by:
l=2πr
- From this, we can express the radius r in terms of l:
r=l2π
- The area A1 of the circle is:
A1=πr2=π(l2π)2=l24π
- The perimeter of the square is given by:
4x=l⟹x=l4
- The area A2 of the square is:
A2=x2=(l4)2=l216
- The magnetic moment M for a loop is given by:
M=I⋅A
- For the circle, the magnetic moment M1 is:
M1=I1⋅A1=I1⋅l24π
- For the square, the magnetic moment M2 is:
M2=I2⋅A2=I2⋅l216
- Given that the currents are in the ratio:
I1I2=45
- We can express I1 in terms of I2:
I1=45I2
- Now substituting I1 into the expression for M1:
M1=(45I2)⋅l24π=4I2l220π=I2l25π
- Now we can find the ratio of the magnetic moments:
M1M2=I2l25πI2⋅l216=15π⋅16l2=165π
- Therefore, the ratio of the effective magnetic moments is:
M1M2=165π
The ratio of their effective magnetic moments is 165π.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-II
79 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
3 Videos
Similar Questions
Two identical wires AandB , each of length 'l', carry the same current I. Wire A is bent into a circle of radius RandwireB is bent to form a square of side 'a' . If BAandBB are the values of magnetic field at the centres of the circle and square respectively , then the ratio BABB is :
View SolutionTwo identical wires AandB , each of length 'l', carry the same current I. Wire A is bent into a circle of radius RandwireB is bent to form a square of side 'a' . If BAandBB are the values of magnetic field at the centres of the circle and square respectively , then the ratio BABB is :
View SolutionA wire is looped in the form of a circle of radius 28 cm. It is re-bent into a square form. Determine the length of the side of the square.
View SolutionA wire is looped in the form of a circle of radius 28 cm. It is re-bent into a square form. Determine the length of the side of the square.
View SolutionA wire of length l is cut into two parts. One part is bent into a circle and the other into a square. Prove that the sum of the areas of the circle and the square is the least, if the radius of the circle is half of the side of the square.
View SolutionTwo wires A and B are of lengths 40 cm and 30 cm. A is bent into a circle of radius r and B into an arc of radius r. A current i1 is passed through A and i2 through B. To have the same magnetic induction at the centre, the ratio of i1 : i2 is
View SolutionA wire is bent in the form of a circular arc of radius r with a straight portion AB. If the current in the wire is i, then the magnetic induction at point O is
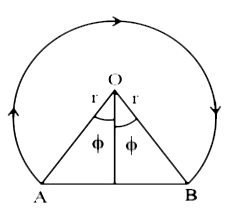
View SolutionA current of I amperes is flowing through each of the bent wires as shown. Find the magnitude of magnetic field at O.
View SolutionA wire is bent in the form of a circular arc with a straight portion AB. Magnetic induction at O when current flowing in the wire, is

View SolutionA circular loop and a square loop are formed from the same wire and the same current is passed through them . Find the ratio of their dipole moments.
View Solution
