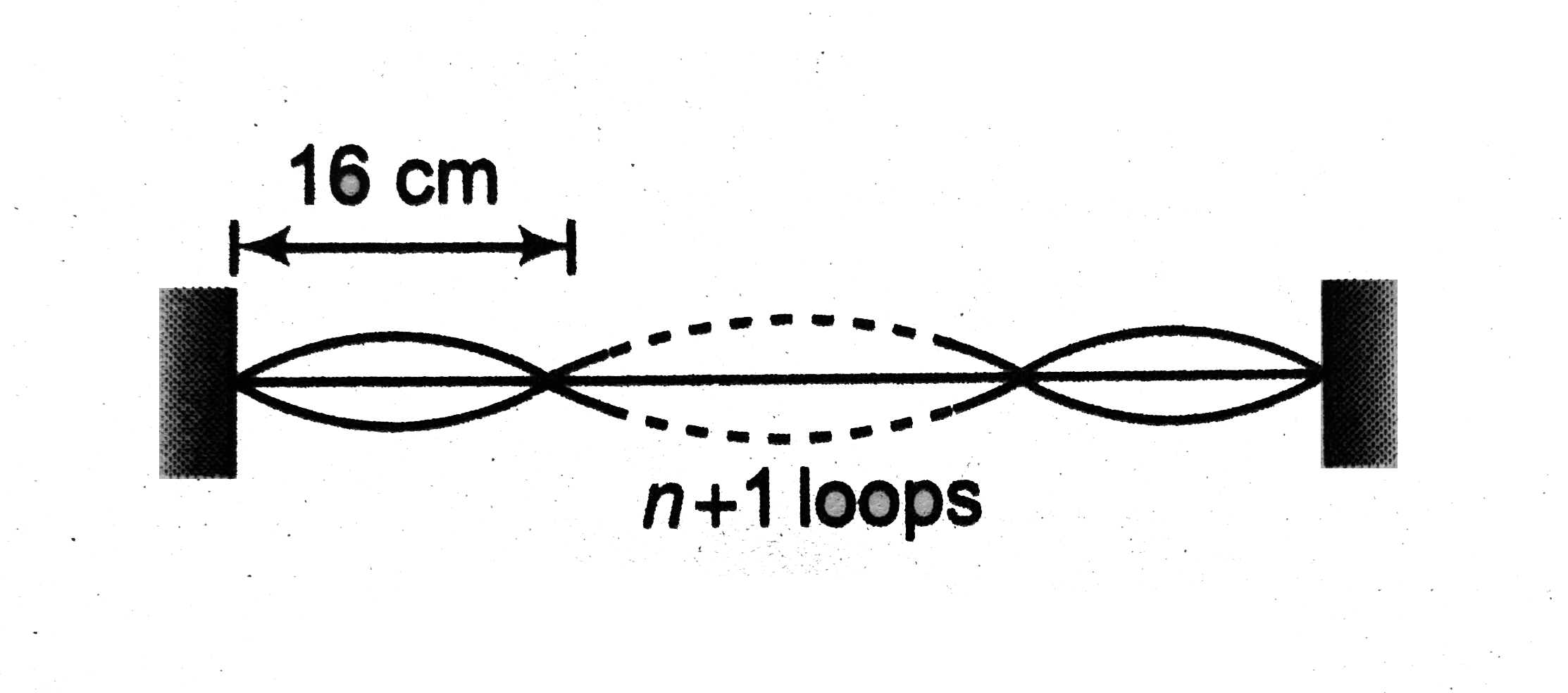
A string fixed at both ends has consecutive standing wave modes for which the distances between adjacent nodes are 18 cm and 16 cm, respectively.
(a) What is the minimum possible length of the string?
(b) If the tension is 10 N and the linear mass density is 4 g/m, what is the fundamental frequency?
The correct Answer is:A, B, C, D
(a) 
Let l be the length of the string. Then,
………………(i)
16(n+1)=l…………..(ii)
From Eqs. (i) and (ii), we get
n=8
and l=144 cm
Therefore, the minimum possible length of the string can be 144 cm.
(b) For fundamental frequency,
or
=288 m
Speed of wave on the string,
=17.36 Hz

Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Exercise 18.13videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Exercise 18.24videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Example Type 41videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.74videos
SOUND WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary30videos
THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
Similar Questions
A string fixed at both ends has consecutive standing wave modes for which the distances between adjacent nodes are 18 cmand16 cm respectively. The minimum possible length of the string is:
View SolutionWhat is maximum possible wavelength of standing waves in 1m long string if it is fixed at both ends
View SolutionA string fastened at both ends has successive resonances with wavelengths of 0.54 m for nth harmonic and 0.48 m for the (n+1) th harmonic and 0.48 m for the (n+1) th harmonic.
(a) Which harmonics are these?
(b) What is the length of the stirng?
(c) What is the wavelength of the fundamental frequency?View SolutionA string, fixed at both ends, vibrates in a resonant mode with a separation of 2.0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1.6 cm. Find the length of the string.
View SolutionA string fixed at both ends is 8.40m long and has a mass of 0.120kg. It is subjected to a tension of 96.0N and set oscillating. (a) What is the speed of the waves on the string? (b) What is the longest possible wavelength for a standing wave ? (c) Give the frequency of the wave.
View SolutionA string is fixed at both ends. The tension in the string and density of the string are accurately known but the length and the radius of cross section of the string are known with some errorl If maximum errors made in the measurements of length and radius are 1% and 0.5% respectively them what is the maximum possible percentage error in the calculation of fundamental frequencyof the that string ?
View SolutionThe equation of a standing wave, produced on a string fixed at both ends, is y=(0.4cm)sin[(0.314cm−1)x]cos[(600πs−1)t] What could be the smallest length of the string ?
View SolutionA string fixed at both ends, is vibrating in a particular mode of vibration. Vibration is such that a point on string is at maximum displacement and it is at a distance of one fourth of length of string from one end. The frequency of vibration in thus mode is 200Hz. What will be the frequency of vibration when it vibrates in next mode such that the same point is at maximum displacement?
View SolutionThe vibrations of a string of length 60 cm fixed at both ends are represented by the equation y=4sin(πx15)cos(96πt), where x and y are in cm and t in seconds.
(a)What is the maximum displacement of a point at x=5cm?
(b)Where are the nodes located along the string?
(c)What is the velocity of the particle at x=7.5cm and t=0.25s?
(d)Write down the equations of the component waves whose superposition gives the above wave.View SolutionFour pieces of string of length L are joined end to end to make a long string of length 4L. The linear mass density of the strings are μ,4μ,9μand16μ, respectively. One end of the combined string is tied to a fixed support and a transverse wave has been generated at the other end having frequency f (ignore any reflection and absorption). string has been stretched under a tension F. Find the time taken by wave to reach from source end to fixed end.

View Solution

