A string is warapped around a cylinder of mass m and radius r. The string is also connected to a block of same mass m with the help of another pulley as shown in figure. The angular acceleration of the cylinder is ( friction is sufficient for rolling ) ( all pulleys are ideal)

g(2−sinθ)16R
2g(4−sinθ)35R
7g(3−sinθ)25R
g(2−sinθ)12R
The correct Answer is:B
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
41 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A string is wound around a hollow cylinder of mass 5 Kg and radius 0.5 m. If the string is now pulled with a horizontal force of 40 N, the cylinder is rolling without slipping on a horizontal surface (see figure), then the angular acceleration of the cylinder will be (Neglect the mass and thickness of the string).

View SolutionA load of mass m is attached to the end of a string wound on a cylinder of mass M and radius R. The string passes round a pulley.
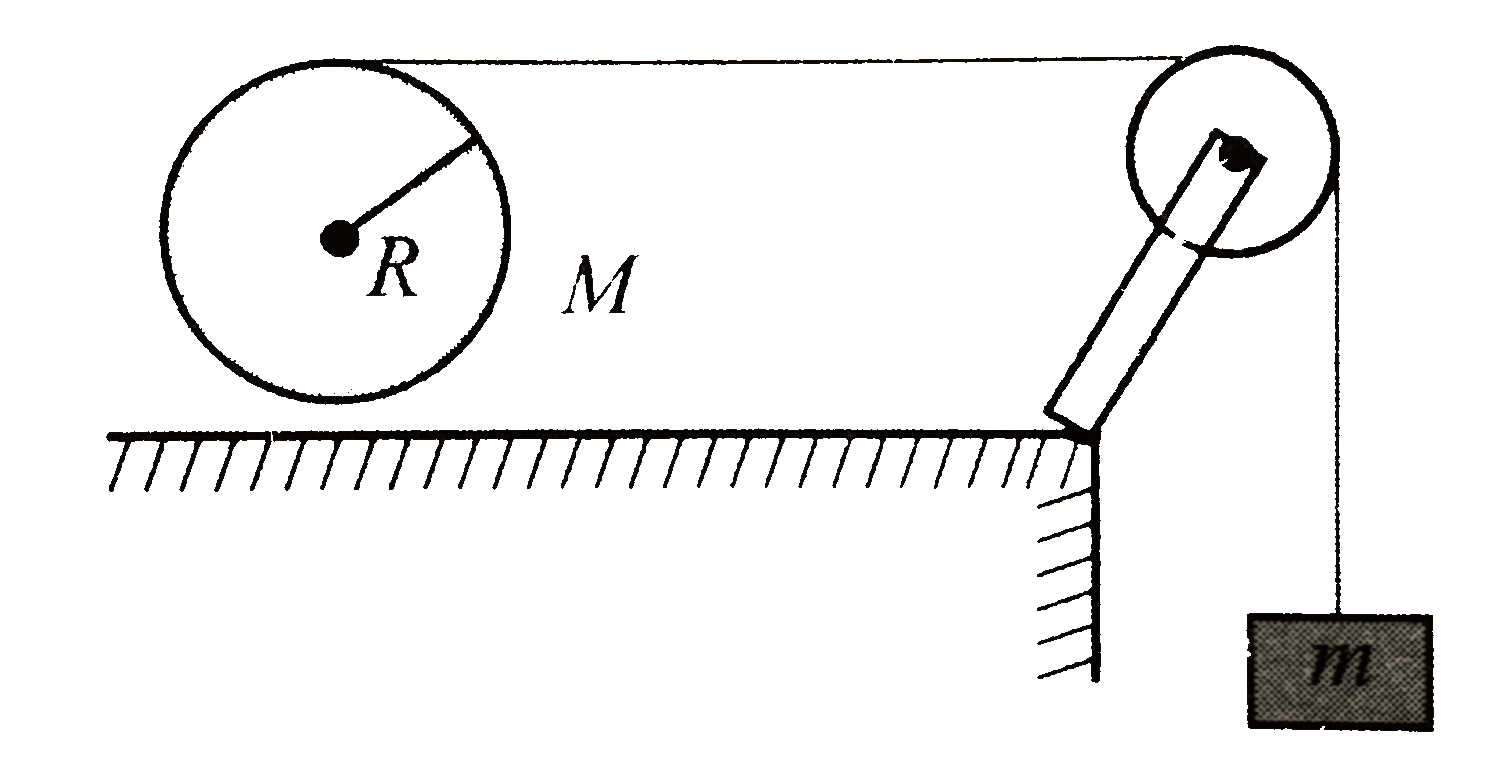
a. Find the acceleration of the cylinder M when it rolls.
b. If the coefficient of friction is μ. Find the accelerative of the cylinder when it slips and rolls.
c. Find the minimum value of coefficient of friction for which the cylinder rolls always
View Solution
Knowledge Check
Angular acceleration of the cylinder C shows in the figure is (all strings and the pulley are ideal)
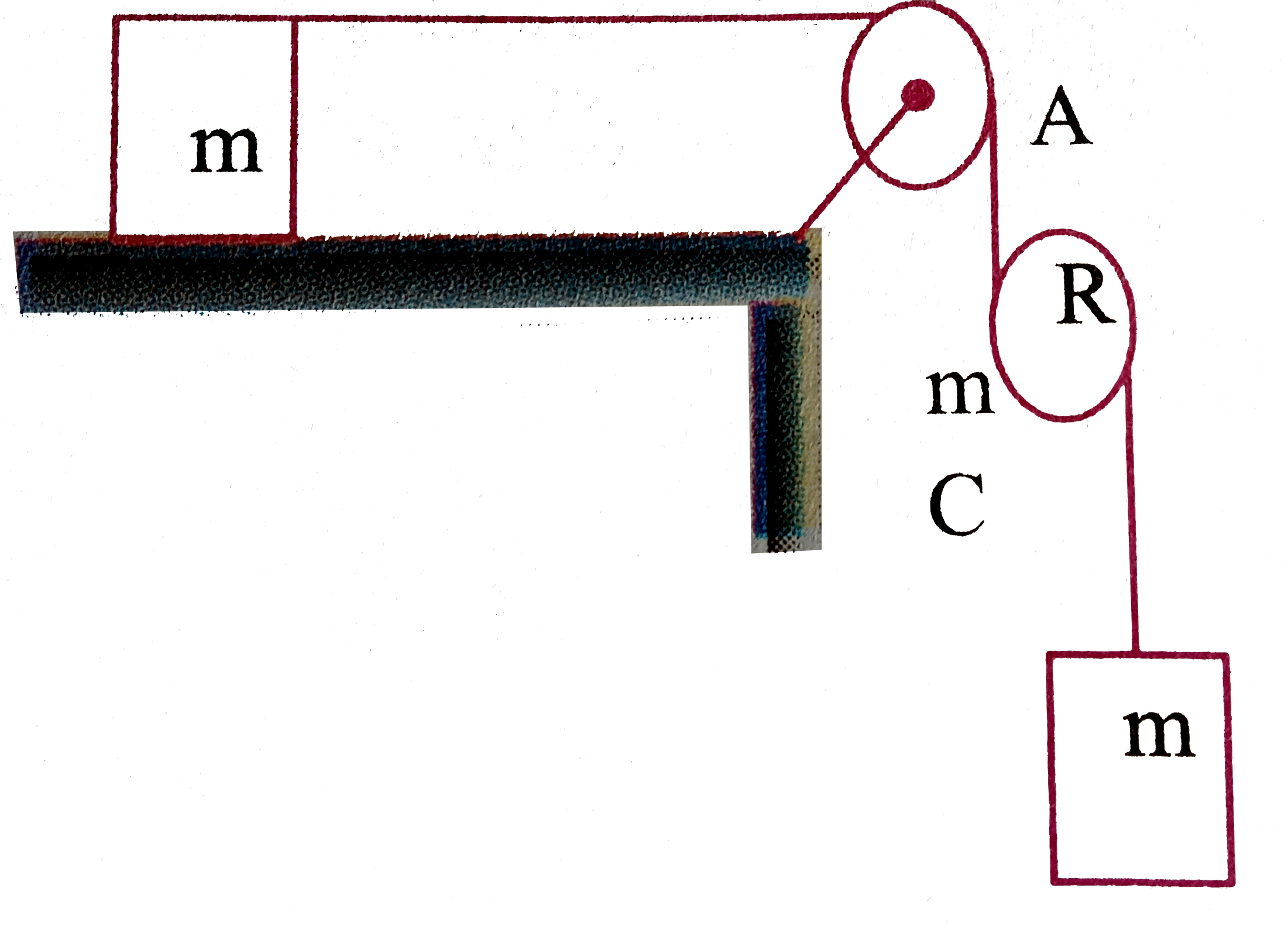 A2g3RB2g5RC2gRDg2R
A2g3RB2g5RC2gRDg2RA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
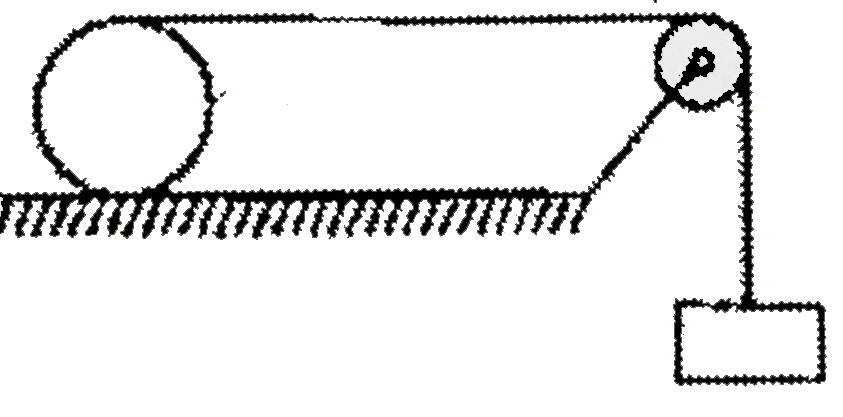
Acceleration of cylinder is:AgBg2Cg4D3g4A string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
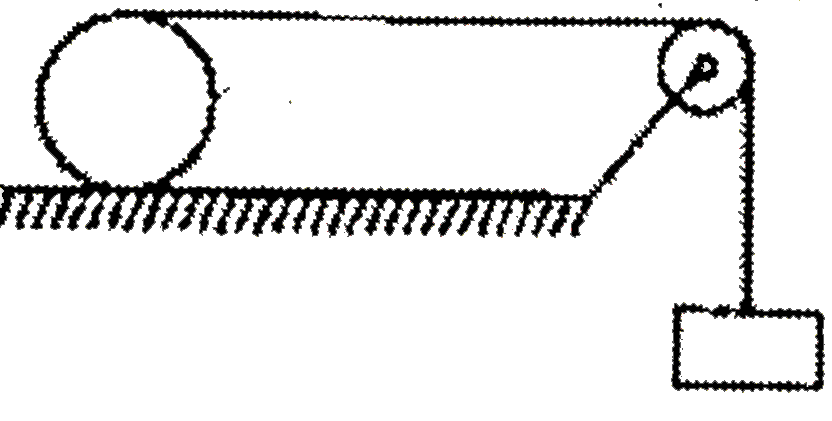
Acceleration of hanging mass is:AgBg2Cg4D3g4
A load of mass m is attached to the end of a string wound on a cylinder of mass M and radius R. The string passes round a pulley.

a. Find the acceleration of the cylinder M when it rolls.
b. If the coefficient of friction is μ. Find the accelerative of the cylinder when it slips and rolls.
c. Find the minimum value of coefficient of friction for which the cylinder rolls always
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
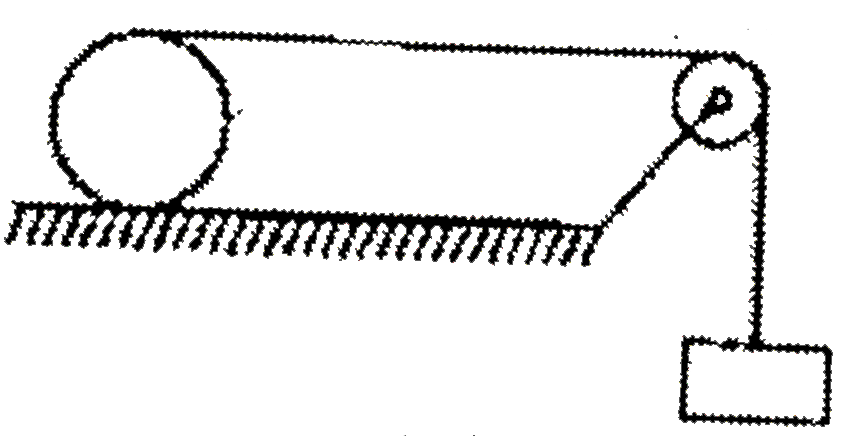
Velocity of hanging block at this moment is: is:
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
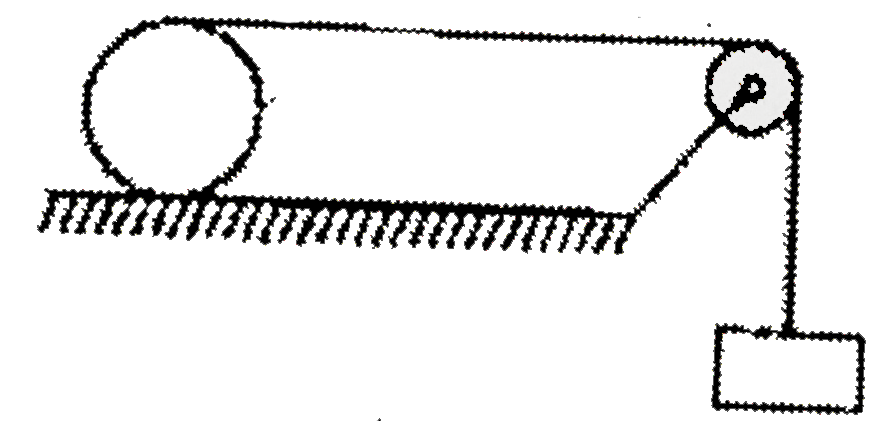
Velocity of point of contact 'of cylinder at this moment is:
View SolutionA string wrapped around a cylinder of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
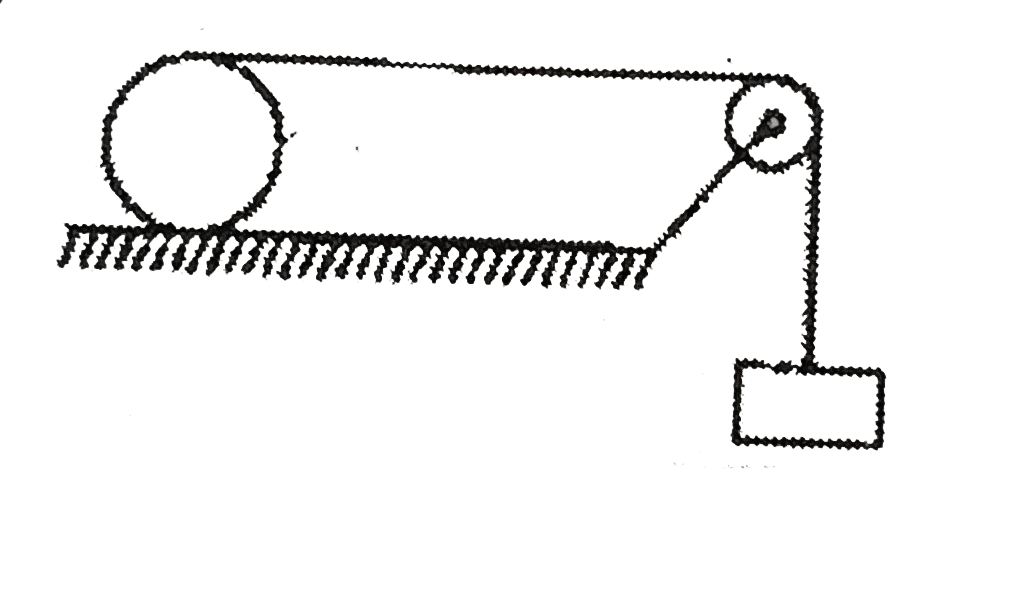
Distance moved by hanging mass during the above time interval is:
View SolutionA block of mass m=5 kg is placed on the wedge of mass M=32 kg as shown in the figure. Find the acceleration of wedge with respect to ground. (Neglect any type of friction. String and pulley are ideal )

View Solution
