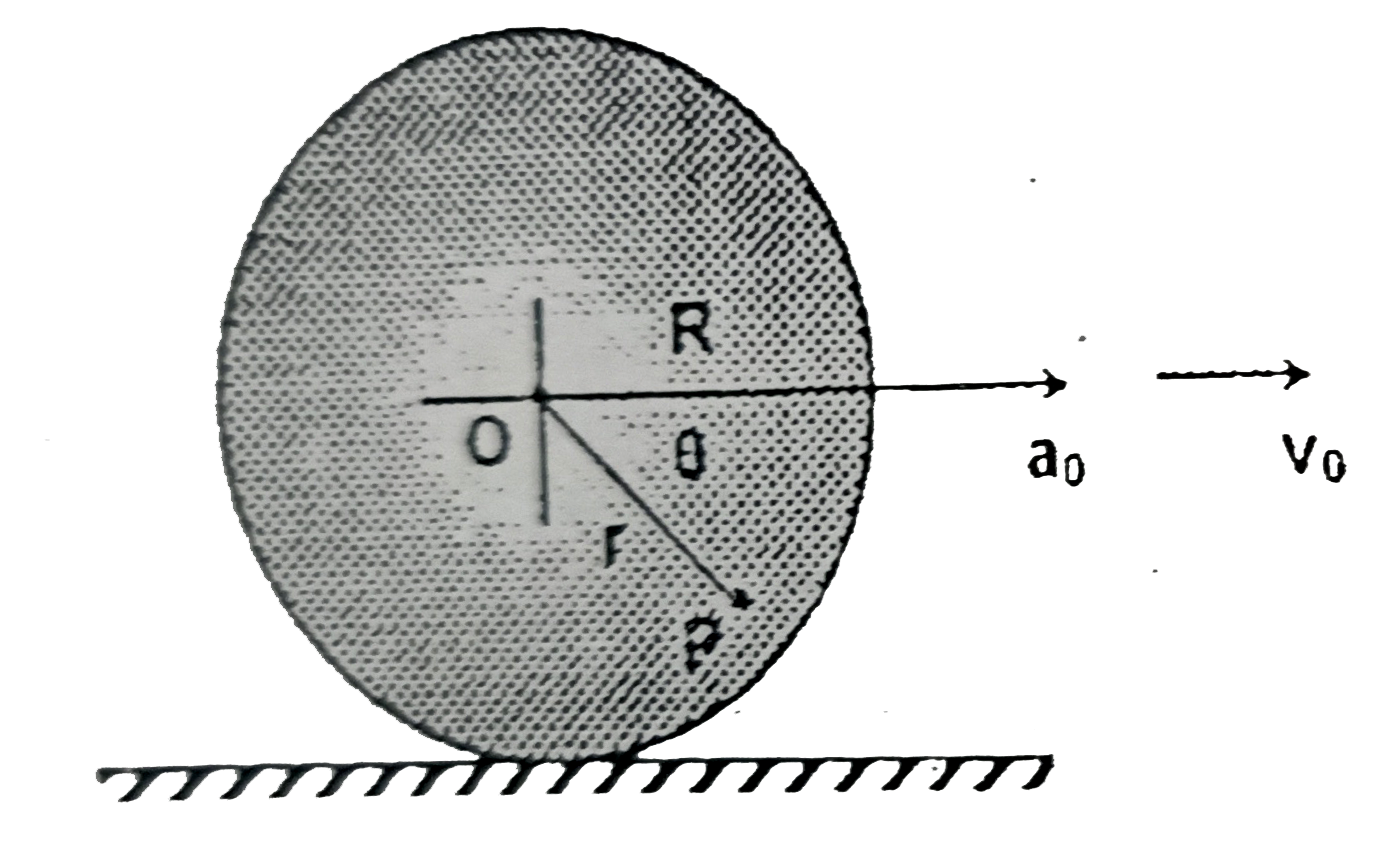
The wheel of radius R rolls wihtout slipping on horizontal rough surface and its centre O has an acceleration a0 in forward direction. A point P on the wheel is a distance r from O and angular position θ from horizontal. Find the angle θ for which point P can have zero acceleration in this position .

cos−1(r)R
tan−1(r)R
sin−1(r)R
cos−1(r)2R
The correct Answer is:C
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
41 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
The wheel of radius R rolls without slipping on horizontal rough surface, and its centre O has an horizontal acceleration a0 in forward direction. A point P on the wheel is a distance r from O and angular position θ from horizontal. For a given values of a0, R and r, determine the angle θ for which point P has no acceleration in this position.
View SolutionA wheel of radius R rolls without slipping on the horizontal surface with speed v0. When the contact point is P on the road, a small patch of mud separates from the wheel at its highest point strikes the road at point Q. Find distance PQ.
View Solution
Knowledge Check
The wheel of radius R rolls with out slipping on horizontal rough surface, and its centre O has an horizontal acceleration in a0 forward direction. A point P on the wheel is a distancer r from O and angular position θ from horizontal. For the given values of a0 R and r, determine the angle θ for which point P has no acceleration in this position.
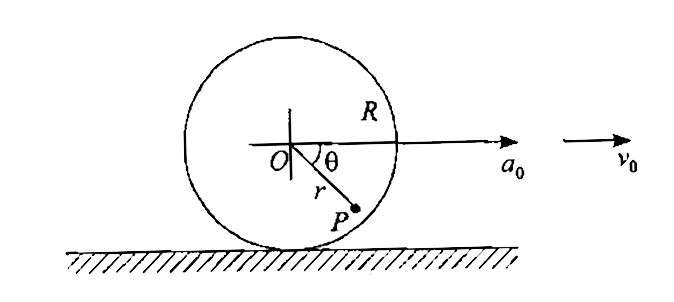 Acos1.rRBtan1.rRCsin1.rRDcos1.r2R
Acos1.rRBtan1.rRCsin1.rRDcos1.r2RA wheel of radius R rolls without slipping on a horizontal ground. The distance travelled by a point on the rim in one complete rotation is:
A2πRB8RC2RDπRA wheel of radius r rolls without slipping with a speed v on a horizontal road. When it is at a point A on the road, a small blob of mud separates from'the wheel at- its highest point and lands at point B on the road:
AAb=v√rgBAB=2v√rgCAB=4v√rgDIf v>√4rg, the blob of mud land on the wheel and not on the road.
A wheel of radius r rolls without slipping with a speed v on a horizontal road. When it is at a point A on the road, a small blob of mud separates from'the wheel at- its highest point and lands at point B on the road:
View SolutionA wheel of radius r rolls without slipping with a speed v on a horizontal road. When it is at a point A on the road, a small blob of mud separates from'the wheel at- its highest point and lands at point B on the road:
View SolutionA disc of radius r rolls without slipping on a rough horizontal floor. If veloocity of its centre of mass is v0, then velocity of point P, as shown in the figure
(OP=r/2 and ∠QOP=60∘)is

View SolutionConsider a wheel rolls without slipping and its centre moves with constant acceleration a. Find the acceleration of points O,P,Q and S when linear velocity of the centre of wheel is v.
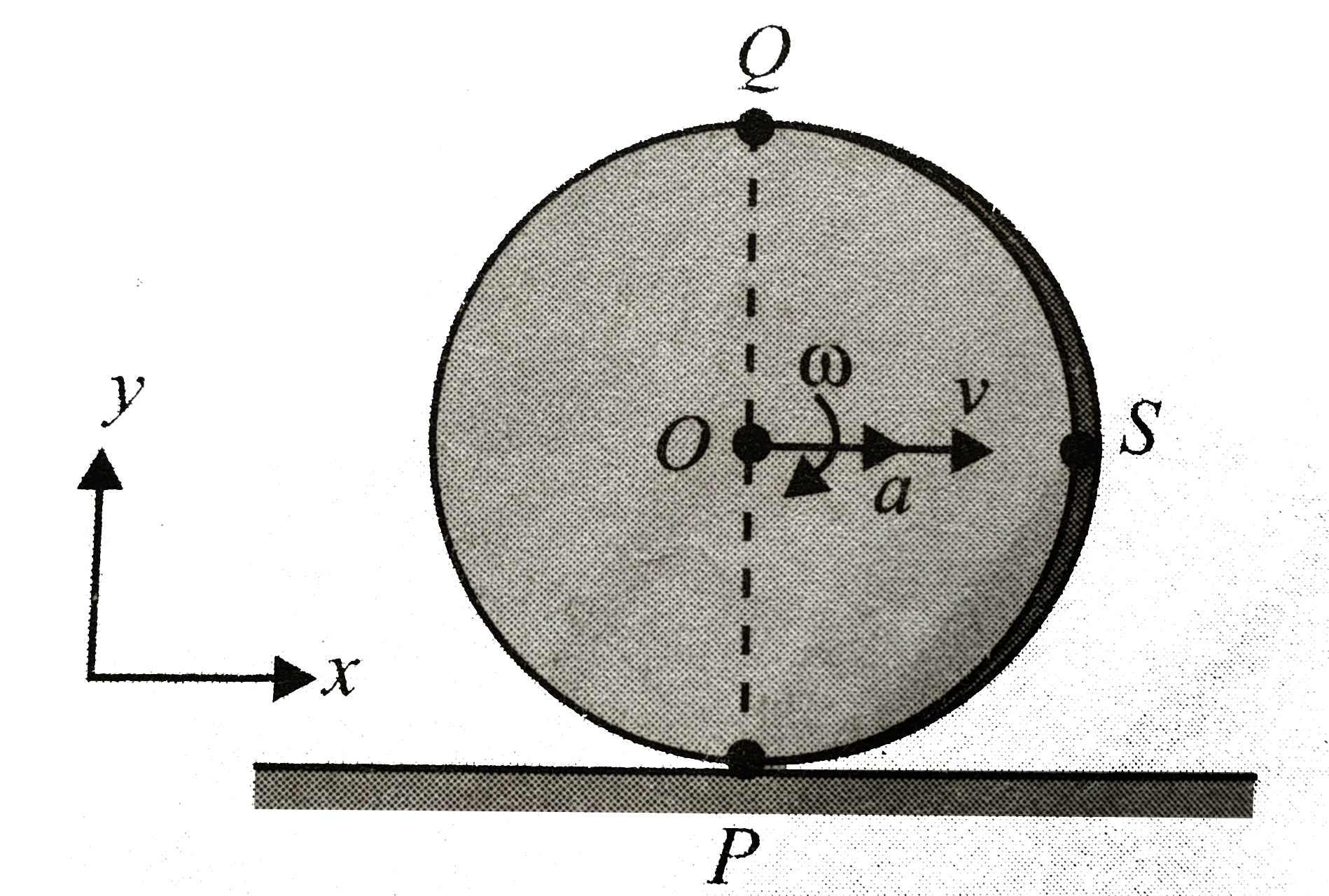
View SolutionA disc of radius r rolls without slipping on a rough horizontal floor. If veloocity of its centre of mass is v0, then velocity of point P, as shown in the figure
(OP=r/2 and ∠QOP=60∘)is

View Solution
