A string is wrapped over the edge a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
The correct Answer is:B, C
Let the radius of the disc =R
Therefore according to the question and ure
mg−T=ma
and the toque about the centre
=T×R=1×α
→T×R=12mR2×aR
→T=12ma………..2
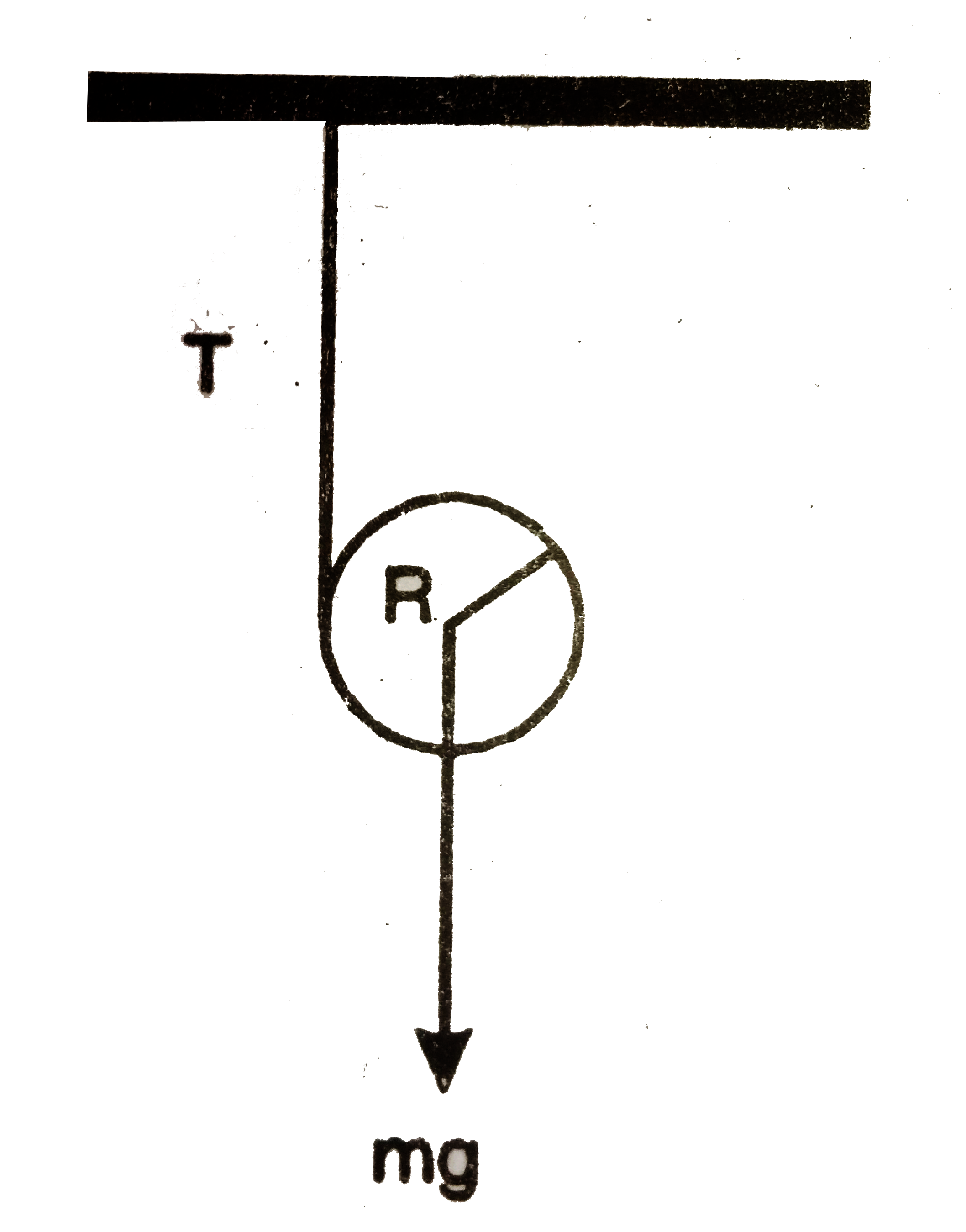
Putting this value in the equation 1 we get
→mg−12ma=ma
→mg=32ma
⇒a=2g3
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 2
15 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
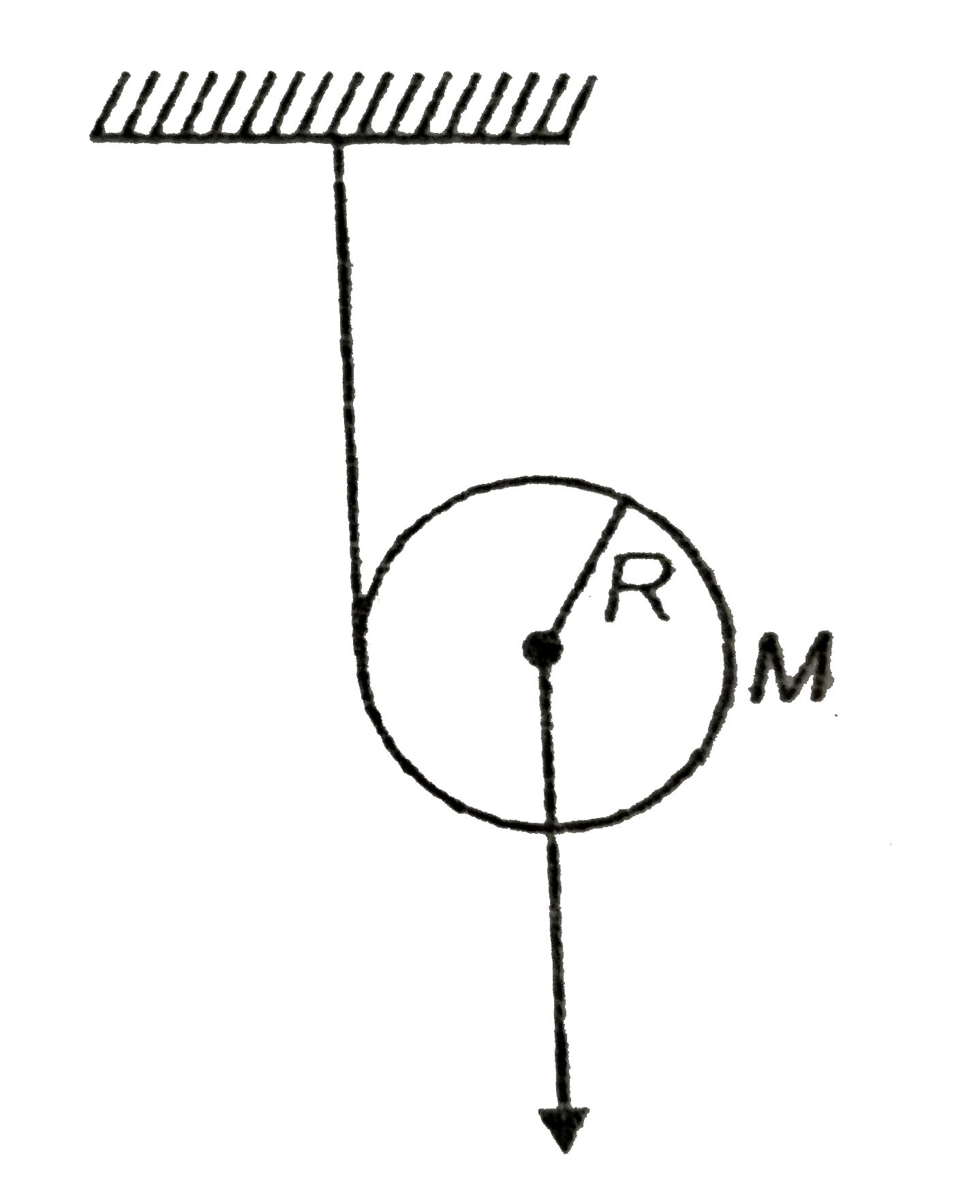
A disc of mass M has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the ceiling and the disc is released from rest. Find the acceleration of the disc and the tension in the string.
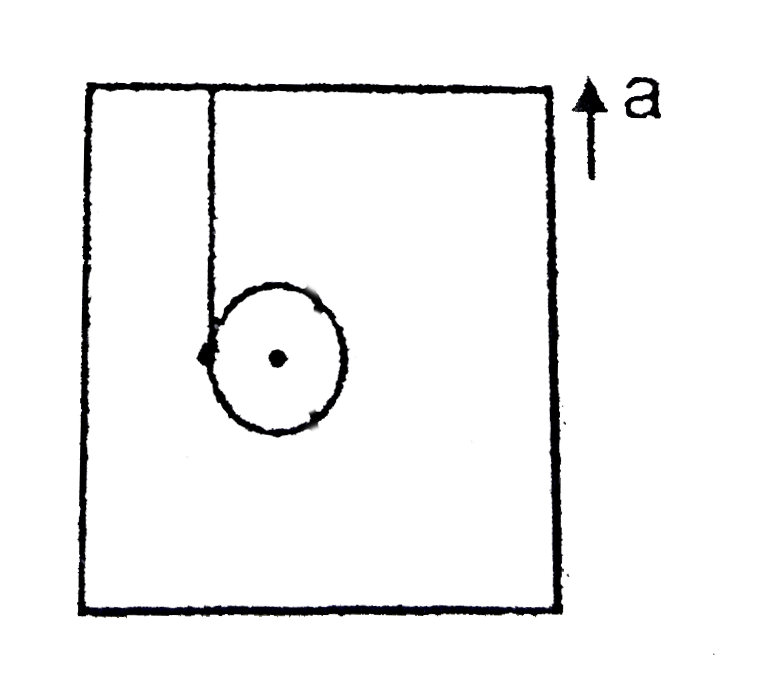
View SolutionIn the figure shown a thin light inextensible string is wrapped around a uniform disc. One end of the strin is fixed to the ceiling of the lift and the other end is fied to the circumference of the disc. Acceleration 'a' of the lift is such that the centre of the disc not move with respect to ground. Find the value of ag. String does not slip on pulley.
View Solution
Knowledge Check
A string is wrapped several times round a solid cylinder. Then free end of the string is held stationary. If the cylinder is released to move down, then the acceleration of that cylinder is
Ag/3Bg/2C3g/2D2g/3A uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
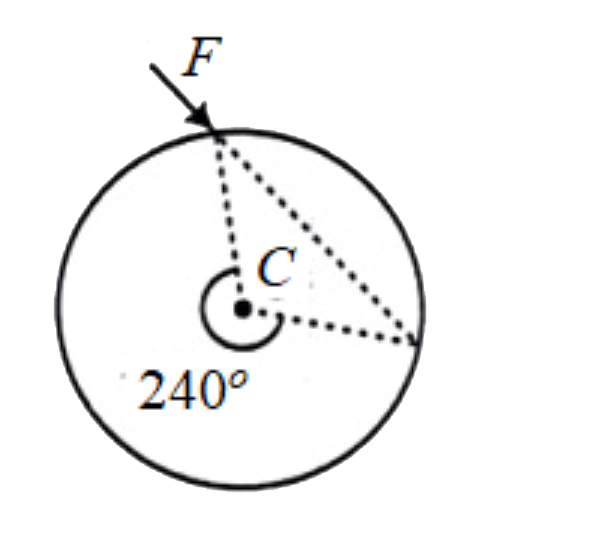 A√3FMRBFMRC2√3FMRDF2MR
A√3FMRBFMRC2√3FMRDF2MRA string is wrapped on a uniform disc and the other end of the string connected to a wall. The system is placed on a smooth plane, inclined at an angle θ, with the string parallel to the plane, as shown in the figure. The acceleration of the disc is
 A13gsinθB12gsinθC23gsinθD13gsinθ
A13gsinθB12gsinθC23gsinθD13gsinθ
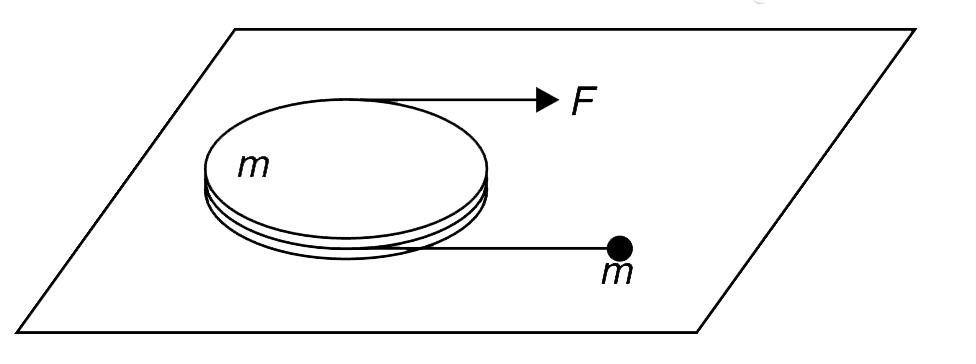
A disc of mass m lies flat on a smooth horizontal table. A light string runs halfway around it as shown in figure. One end of the string is attached to a particle of mass m and the other end is being pulled with a force F. There is no friction between the disc and the string. Find acceleration of the end of the string to which force is being applied.
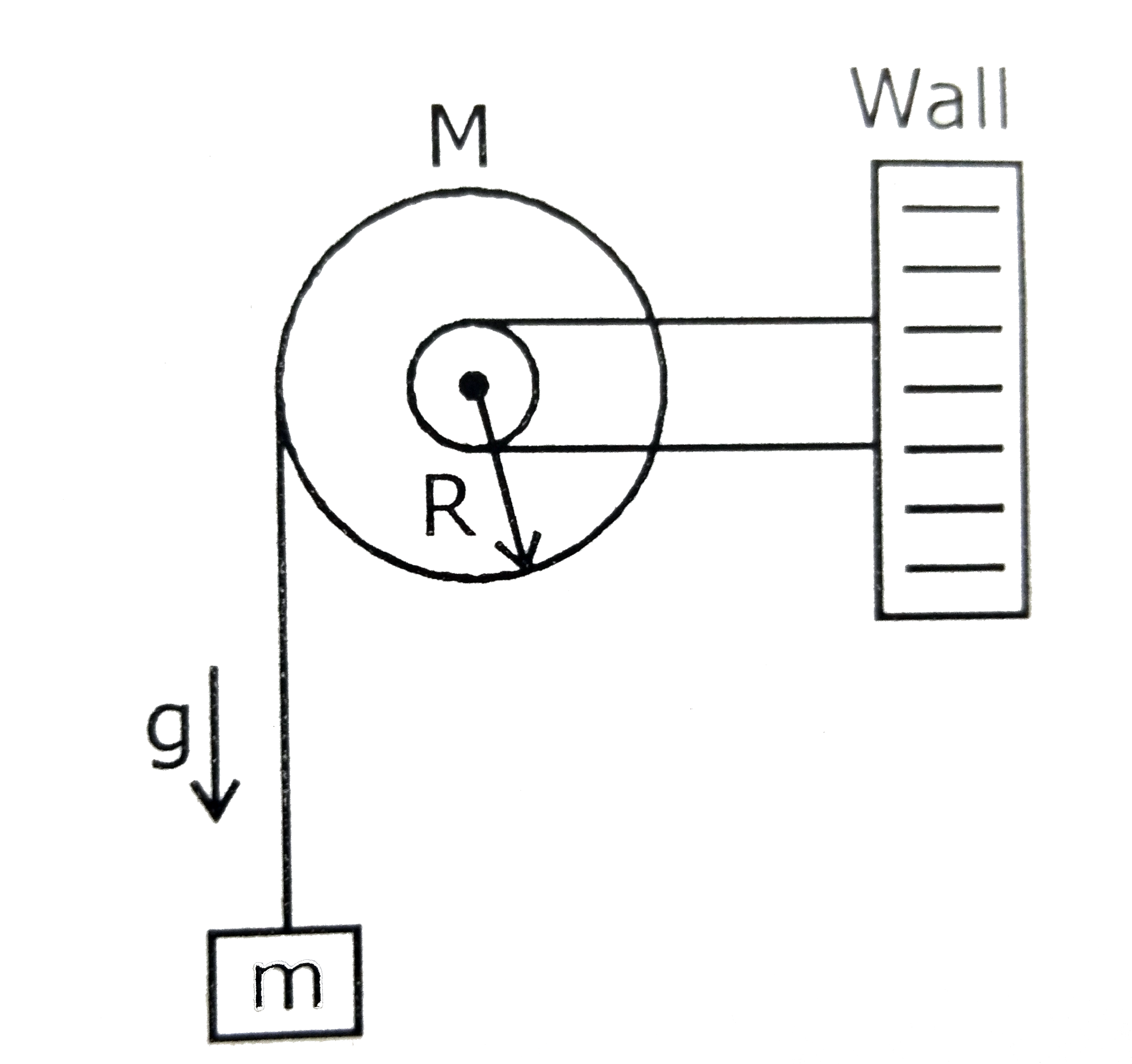
View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is
View SolutionTwo wooden disc , one with radius 2 cm and mass 1 kg and the other with radius 4 cm and mass 2 kg , are welded together coaxially and mounted on a frictionless axis through their common centre. Alight string is wrapped around the edge of the smaller disc, and a 3 kg block is suspended from the free end of the string.What is the acceleration of the block after it is released? Repeat the above process if the stringi swrapped around the edge of the larger disc.
View SolutionA solid cylinder has a thin string wrapped several times around its circumference. The string is fixed at one end and the cylinder is released. Find the downward acceleration of cylinder and tension in the string.
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
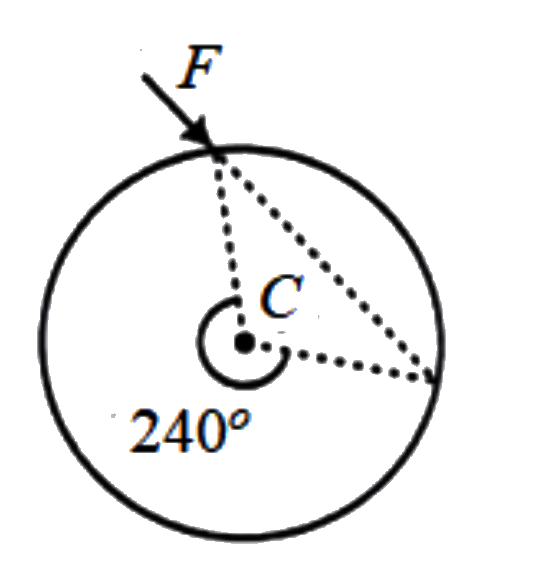
View Solution
