A sunshine recorder globe is a device that provides the information about climate and weather by recording the amount of sunshine for a given location. One such globe of diameter 20 cm and refractive index 1.5 is used for the purpose. A parallel beam of light enters the globe and is refracted by the spherical surface of the globe. Determine the position of the image of the rays formed.
To solve the problem of determining the position of the image formed by a sunshine recorder globe, we will follow these steps:
Step 1: Identify Given Data
- Diameter of the globe (D) = 20 cm
- Radius of the globe (R) = D/2 = 10 cm
- Refractive index of the globe (n) = 1.5
- Refractive index of air (n1) = 1.0
- The object is a parallel beam of light, which means the object distance (u) = -∞ (since it is considered to be coming from a very far distance).
Step 2: Use the Lens Maker's Formula
The formula for refraction at a spherical surface is given by:
n2v−n1u=n2−n1R
Where:
- n1 = refractive index of the first medium (air) = 1.0
- n2 = refractive index of the second medium (globe) = 1.5
- R = radius of curvature = 10 cm (positive as the center of curvature is on the same side as the incoming light)
Step 3: Substitute Values for First Refraction
Substituting the values into the formula:
1.5v−1.0−∞=1.5−1.010
Since 1.0−∞ approaches 0, the equation simplifies to:
1.5v=0.510
1.5v=0.05
Now, solving for v:
v=1.50.05=30 cm
This means that the image formed after the first refraction is at a distance of 30 cm from the center of the globe.
Step 4: Determine Object Distance for Second Refraction
The image formed at 30 cm is now the object for the second refraction. The distance from the center of the globe to this image is 30 cm, and since the radius of the globe is 10 cm, the object distance u for the second refraction is:
u=30 cm−20 cm=10 cm (but it is on the same side, so it is -10 cm)
Step 5: Apply Lens Maker's Formula for Second Refraction
Now we apply the lens maker's formula again for the second refraction:
n1v−n2u=n1−n2R
Where:
- n1=1.0
- n2=1.5
- u=−10 cm
- R=−10 cm (negative because the center of curvature is on the opposite side)
Substituting the values:
1.0v−1.5−10=1.0−1.5−10
This simplifies to:
1.0v+0.15=−0.05
1.0v=−0.05−0.15=−0.20
Now solving for v:
v=1.0−0.20=−5 cm
This means the final image is located 5 cm on the same side as the object.
Step 6: Conclusion
The position of the image formed by the rays after passing through the sunshine recorder globe is 5 cm from the center of the globe, on the same side as the incoming light.
---
- Diameter of the globe (D) = 20 cm
- Radius of the globe (R) = D/2 = 10 cm
- Refractive index of the globe (n) = 1.5
- Refractive index of air (n1) = 1.0
- The object is a parallel beam of light, which means the object distance (u) = -∞ (since it is considered to be coming from a very far distance).
The formula for refraction at a spherical surface is given by:
n2v−n1u=n2−n1R
Where:
- n1 = refractive index of the first medium (air) = 1.0
- n2 = refractive index of the second medium (globe) = 1.5
- R = radius of curvature = 10 cm (positive as the center of curvature is on the same side as the incoming light)
Substituting the values into the formula:
1.5v−1.0−∞=1.5−1.010
Since 1.0−∞ approaches 0, the equation simplifies to:
1.5v=0.510
1.5v=0.05
Now, solving for v:
v=1.50.05=30 cm
This means that the image formed after the first refraction is at a distance of 30 cm from the center of the globe.
The image formed at 30 cm is now the object for the second refraction. The distance from the center of the globe to this image is 30 cm, and since the radius of the globe is 10 cm, the object distance u for the second refraction is:
u=30 cm−20 cm=10 cm (but it is on the same side, so it is -10 cm)
Now we apply the lens maker's formula again for the second refraction:
n1v−n2u=n1−n2R
Where:
- n1=1.0
- n2=1.5
- u=−10 cm
- R=−10 cm (negative because the center of curvature is on the opposite side)
1.0v−1.5−10=1.0−1.5−10
This simplifies to:
1.0v+0.15=−0.05
1.0v=−0.05−0.15=−0.20
Now solving for v:
v=1.0−0.20=−5 cm
This means the final image is located 5 cm on the same side as the object.
The position of the image formed by the rays after passing through the sunshine recorder globe is 5 cm from the center of the globe, on the same side as the incoming light.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (5)3videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (6)3videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (3)18videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
- BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION12videos
SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS
Similar Questions
A glass sphere of diameter 20 cm is constructed with a material of refractive index 1.5. A beam of light strikes the sphere and converges at a point 40 cm behind the pole of a spherical surface. Find the position of the image.
View SolutionA fish bowl of diameter 20 cm is filled with a liquid of refractive index 1.4. A letter O is written on the outer surface of the bowl. Determine the position of the image of the word formed when observed through the bowl from the opposite side.
View Solution
Knowledge Check
- Question 1 - Select One
A parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
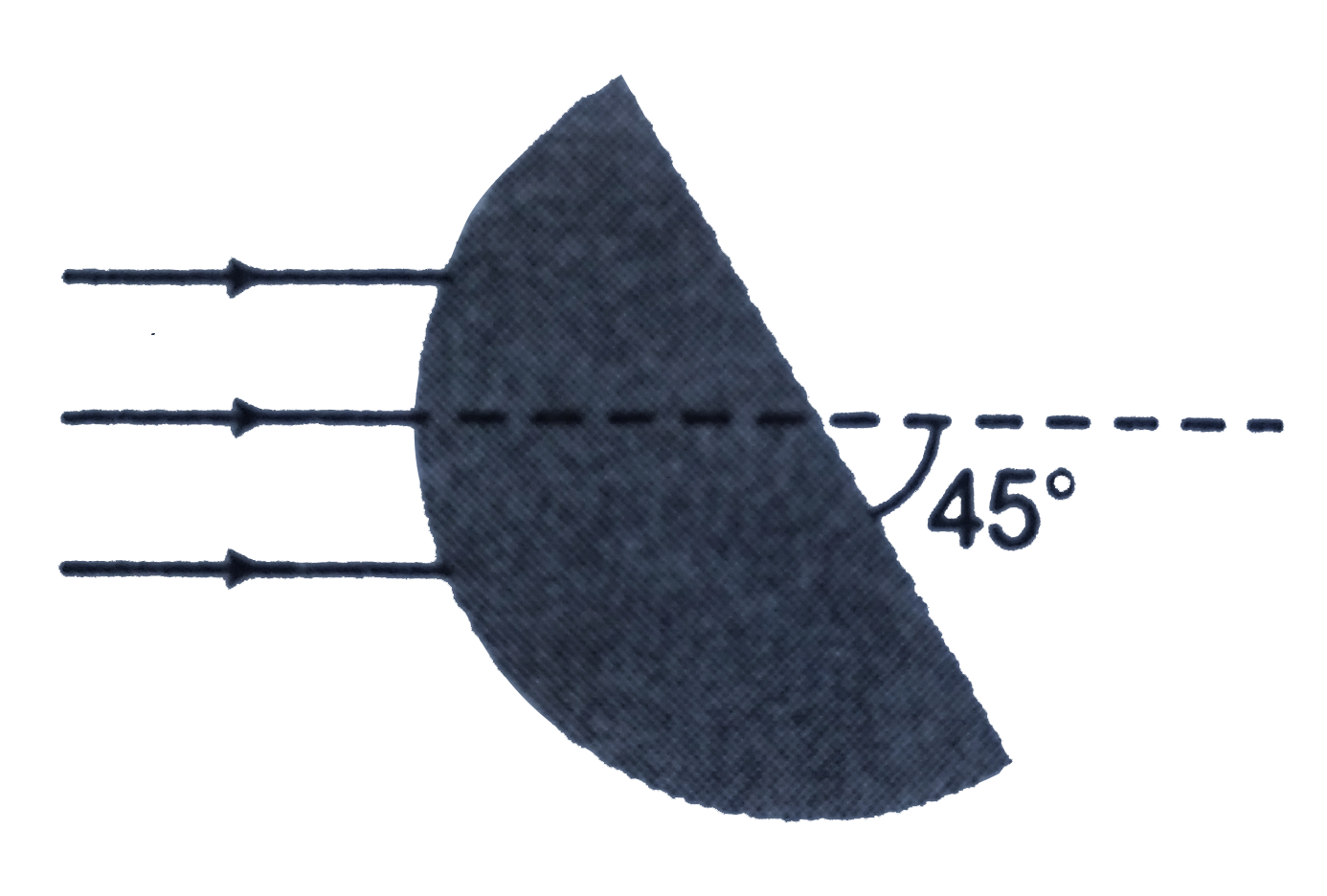 AR2B3RCR3D2R
AR2B3RCR3D2R - Question 2 - Select One or More
A parallel beam of light is incident normally on the flat surface of a hemisphere of radius 6cm and refractive index 1.5, placed in air as shown in figure (i). Assume paraxial ray approxiamtion.
 .AThe rays are focused at 12cm from the point P to the right, in the solutation as shown in figure (i)BThe rays are focused at 16cm from the point P to the right, in the situation as shown in figure (i).CIf the rays are incident at the curved surface (figure (ii)) then these are focused at distance 18cm from point P to the rightDIf the ray are incident at the curved surface (figure(ii)) then these are focused at distance 14cm from point P to the right.
.AThe rays are focused at 12cm from the point P to the right, in the solutation as shown in figure (i)BThe rays are focused at 16cm from the point P to the right, in the situation as shown in figure (i).CIf the rays are incident at the curved surface (figure (ii)) then these are focused at distance 18cm from point P to the rightDIf the ray are incident at the curved surface (figure(ii)) then these are focused at distance 14cm from point P to the right. - Question 3 - Select One or More
Parallel rays of light are falling on convex sphere surface of radius of curvature R = 20 cm as show. Refractive index of the medium is μ=1.5. A refraction from the spherical surface parallel rays
 Aactually meet at some pointBappear to meet after extending the refracted rays backwardsCmeet (or appear to meet) at a distance of 30 cm from the spherical surfaceDmeet (or appear to meet) at a distance of 60 cm from the spherical surface.
Aactually meet at some pointBappear to meet after extending the refracted rays backwardsCmeet (or appear to meet) at a distance of 30 cm from the spherical surfaceDmeet (or appear to meet) at a distance of 60 cm from the spherical surface.
A pin is placed 10cm in front of a convex lens of focal length 20cm, made of a material having refractive index 1.5 . The surface of lens farther away from the pin is silvered and has a radius of curvature 22cm. Determine the position of the final image. Is the image real or virtual?
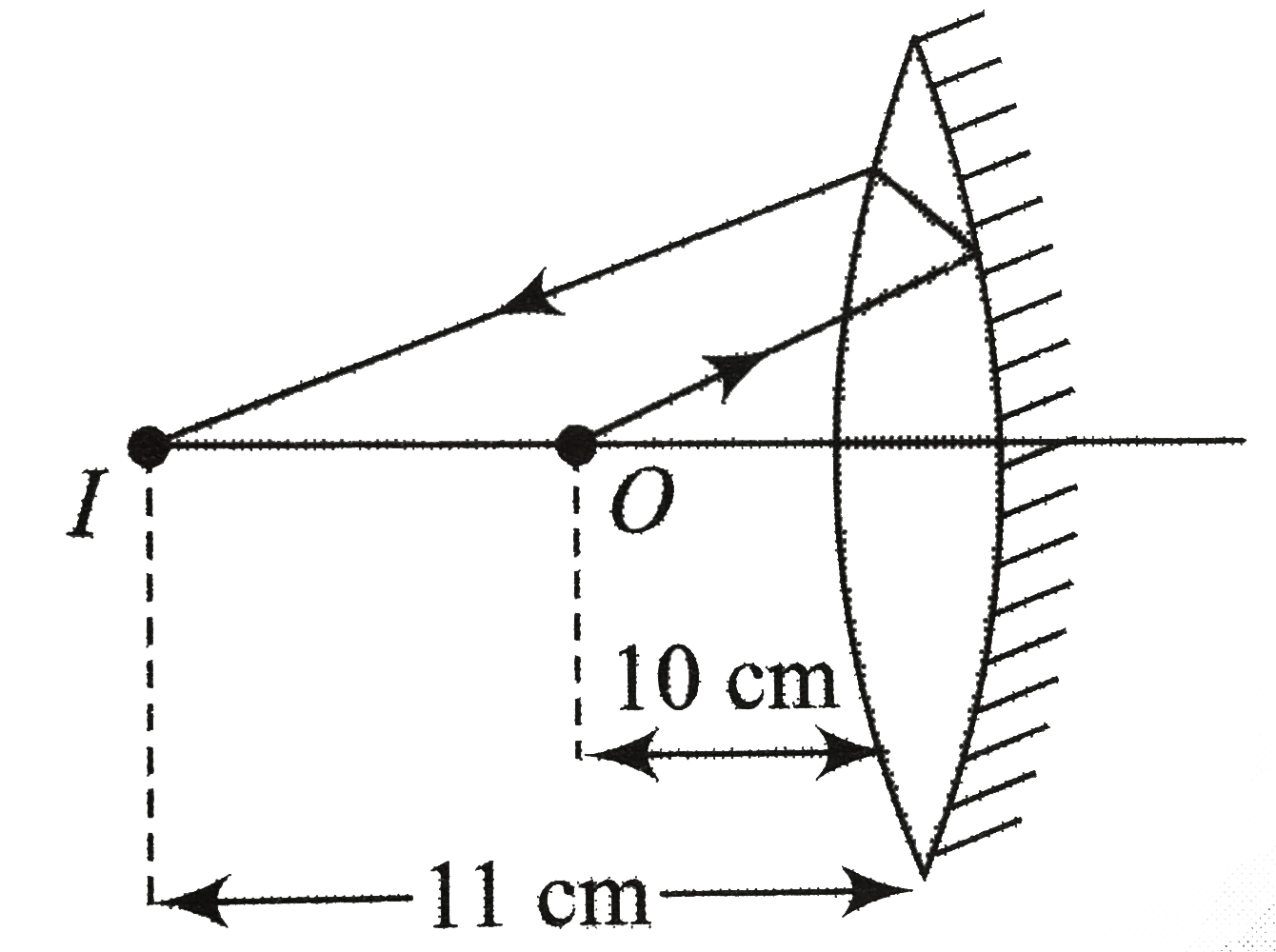 View Solution
View SolutionA biconvex lens has a refractive index of 1.5. The parallel beam of light incident on it forms an image at a distance of 12 cm. Calculate the radii of curvature of both the surfaces if the ratio of the radii of curvature is 2:3.
View SolutionA sunshine recorder globe of 30cm diameter is made of glass of μ=1.5. A ray enters the globe parallel to its axis. Find the position from the centre of the sphere, where the ray crosses the axis.
View SolutionA parallel beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index 2.0 as shown in figure. The position of the image formed by refraction at the first surface is :
 View Solution
View SolutionA glass sphere, refractive index 1.5 and radius 10cm, has a spherical cavity of radius 5cm concentric with it. A narrow beam of parallel light is directed into the sphere. Find the final image and its nature.
 View Solution
View Solution

