A surface of a prism having refractive index 1.5 is covered with a liquid of refractive index . When be the minimum angle of incidence of an incident ray so that on the other surface of the prism the the ray will be totally reflected from the surface covered with liquid? The refracting angle of the prism
Let the critical angle between the prism and the liquid be . If the ray of light is totally reflected from the surface covered with liquid then the angle of incidence of the ray on the surface is [Fig 2.63].
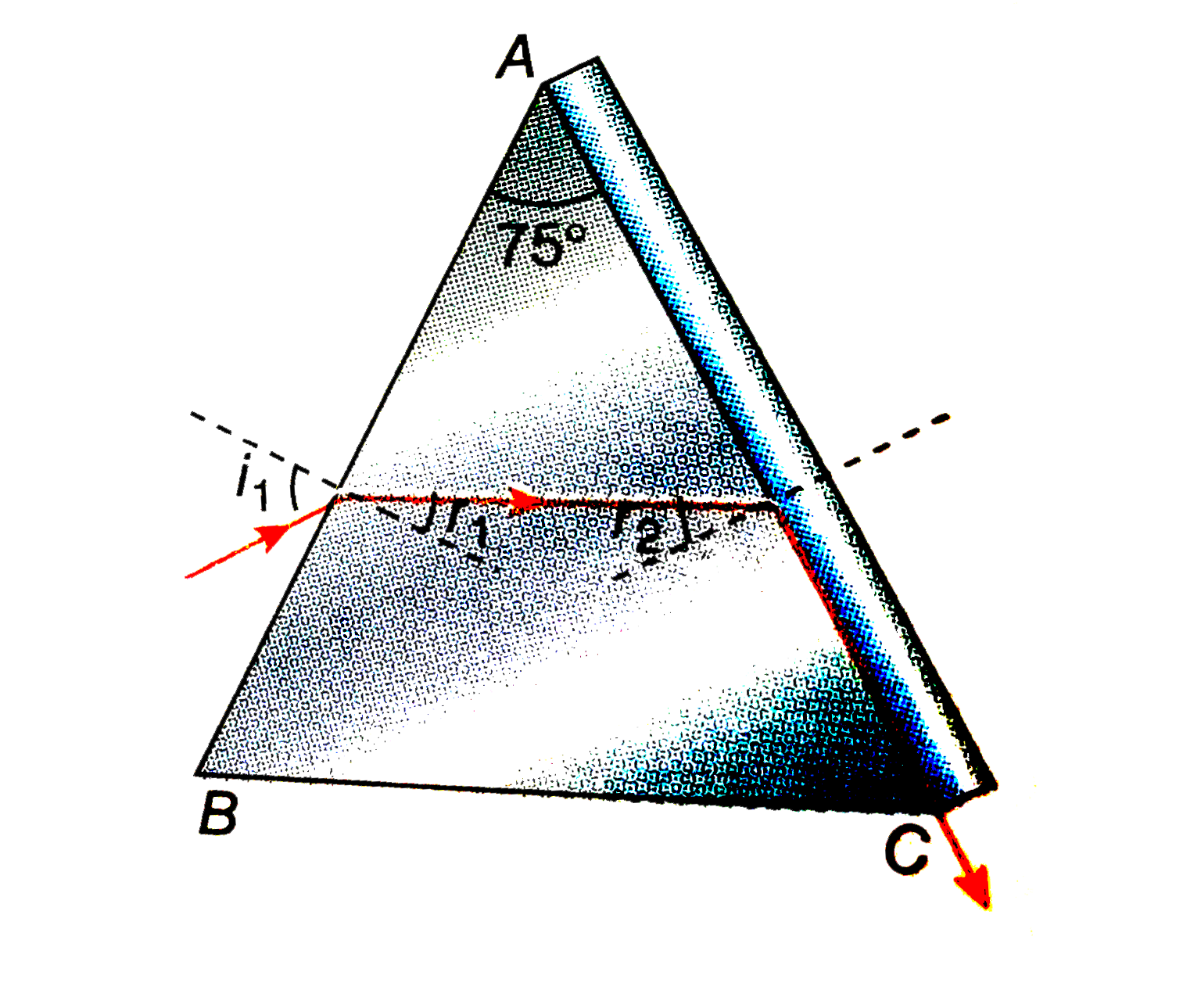
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - HIGHER ORDER THINKING SKILL (HOTS QUESTION)
25 Videos
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - SECTION RELATED QUESTION
18 Videos
- REFLECTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFLECTION OF LIGHTEXERCISE - INTEGER ANSWER TYPE
3 Videos
- SEMICONDUCTORS AND ELECTRONICS BOOK - CHHAYA PUBLICATIONCHAPTER - SEMICONDUCTORS AND ELECTRONICS EXERCISE - CBSE SCANNER
31 Videos
Similar Questions
One face of a prism of refractive index 1.5 and angle 75∘ is covered with a liquid of refractive index 3√24. What should be the angle of incidence of light on the clear face of prism for which light is just totally reflected at the liquid covered face ?
View SolutionOne face of a prism of refractive index 1.5 and angle 75∘ is covered with a liquid of refractive index 3√24. What should be the angle of incidence of light on the clear face of prism for which light is just totally refracted at the liquid covered face ?
View Solution
Knowledge Check
Refractive index of a prism is √7/3 and the angle of prism is 60∘. The minimum angle of incidence of a ray that will be transmitted through the prism is
A30∘B45∘C15∘D50∘A ray of light suffers minimum deviation when incident on an equilateral prism of refractive index √2 . What is the angle of incidence ?
A30∘B45∘C60∘D90∘Light ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
Asin−1(√3−12)Bsin−1(√2−12)Csin−1(√32)Dsin−1(23√3)
Refractive index of a prism is √7/3 and the angle of prism is 60∘. The minimum angle of incidence of a ray that will be transmitted through the prism is
View SolutionA prism of refractive index √2 has refractive angle 60∘ . Find the angle of incidence so that a ray minimum deviation.
View SolutionLight ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
View SolutionAngle of a prism is 30∘ and its refractive index is √2 and one of the surface is silvered. At what angle of incidence, a ray should be incident on one surface so that after reflection from the silvered surface, it retraces its path ?
View SolutionLight ray is incident on a prism of angle A=60∘and refractive indexμ=√2.the angle of incidence at which the emergent ray grazes the surface is given by
View Solution
