Question

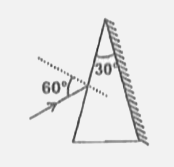
Angle of a prism is ${\displaystyle {30}^{\circ }}$ and its refractive index is ${\displaystyle \sqrt{2}}$ and one of the surface is silvered. At what angle of incidence, a ray should be incident on one surface so that after reflection from the silvered surface, it retraces its path ?

Options

A. (a)`30^@`
B. (b)`60^@`
C. (c)`45^@`
D. (d)`sin^(-1)sqrt(1.5)`

Answer

3

Explanation

To solve the problem step by step, we will follow the principles of optics, particularly focusing on the properties of prisms and reflection.

Step 1: Understand the Geometry of the Prism
We have a prism with an angle \( A = 30^\circ \) and one of its surfaces is silvered. The ray of light will enter the prism, refract, reflect off the silvered surface, and then retrace its path.

Hint: Visualize the prism and the path of the light ray as it enters and reflects.

Step 2: Identify Angles of Refraction
Let \( R_1 \) be the angle of refraction when the light enters the prism, and \( R_2 \) be the angle of refraction when it exits. For the ray to retrace its path after reflecting from the silvered surface, the angle \( R_2 \) must be \( 0^\circ \) (meaning it reflects back along the same path).

Hint: Recall that for a ray to retrace its path, the angle of refraction after reflection must be \( 0^\circ \).

Step 3: Apply the Prism Formula
The relationship between the angles in a prism is given by:
\( A = R_1 + R_2 \)
Since \( R_2 = 0^\circ \), we have:
\( 30^\circ = R_1 + 0^\circ \implies R_1 = 30^\circ \)

Hint: Use the formula for the angles in a prism to find \( R_1 \).

Step 4: Use Snell's Law
Now, we apply Snell's Law at the first surface of the prism:
\( n_1 \sin(i) = n_2 \sin(R_1) \)
where:
- \( n_1 = 1 \) (refractive index of air)
- \( n_2 = \sqrt{2} \) (given refractive index of the prism)
- \( R_1 = 30^\circ \)

Substituting the values, we have:
\( 1 \cdot \sin(i) = \sqrt{2} \cdot \sin(30^\circ) \)
Since \( \sin(30^\circ) = \frac{1}{2} \), we can write:
\( \sin(i) = \sqrt{2} \cdot \frac{1}{2} = \frac{\sqrt{2}}{2} \)

Hint: Remember to substitute the known values into Snell's Law carefully.

Step 5: Solve for the Angle of Incidence
Now, we find the angle of incidence \( i \):
\( \sin(i) = \frac{\sqrt{2}}{2} \)
This corresponds to:
\( i = 45^\circ \)

Hint: Use the inverse sine function to find the angle corresponding to the calculated sine value.

Conclusion
The angle of incidence required for the ray to retrace its path after reflecting from the silvered surface is \( 45^\circ \).

Final Answer: The angle of incidence is \( 45^\circ \).