A system of binary stars of mass mA and mB are moving in circular orbits of radii rA and rB respectively. If TA and TB are at the time periods of masses mA and mB respectively then
If TA>TB, then RA>RB
If TA>TB, then MA>MB
(TATB)2=(RARB)3
TA=TB
The correct Answer is:D
To solve the problem regarding the binary star system, we will follow these steps:
Step 1: Understand the System
We have two stars, A and B, with masses mA and mB respectively, moving in circular orbits of radii rA and rB. The time periods of these stars are TA and TB.
Step 2: Center of Mass Condition
The center of mass (COM) of the system can be defined as:
mArA=mBrB
This equation indicates that the moments about the center of mass are equal. This is our Equation 1.
Step 3: Forces Acting on the Stars
The gravitational force between the two stars provides the necessary centripetal force for their circular motion. The gravitational force Fg is given by:
Fg=GmAmB(rA+rB)2
The centripetal force for star A is:
FcA=mAV2ArA
And for star B:
FcB=mBV2BrB
Since the gravitational force provides the centripetal force, we can set up the following equations:
GmAmB(rA+rB)2=mAV2ArA(2)
GmAmB(rA+rB)2=mBV2BrB(3)
Step 4: Expressing Velocities
The velocities VA and VB can be expressed in terms of the time periods:
VA=2πrATA
VB=2πrBTB
Step 5: Substitute Velocities into the Force Equations
Substituting VA and VB into equations (2) and (3):
GmAmB(rA+rB)2=mA(2πrATA)2rA
GmAmB(rA+rB)2=mB(2πrBTB)2rB
Step 6: Simplifying the Equations
From the first equation:
GmAmB(rA+rB)2=4π2mArAT2A
From the second equation:
GmAmB(rA+rB)2=4π2mBrBT2B
Step 7: Equating the Two Expressions
Since both expressions are equal to the gravitational force, we can set them equal to each other:
4π2mArAT2A=4π2mBrBT2B
This simplifies to:
mArAT2A=mBrBT2B
Step 8: Relating Time Periods
From the center of mass condition mArA=mBrB, we can substitute rB=mAmBrA into the equation:
mArAT2A=mB(mAmBrA)T2B
This leads to:
1T2A=1T2B
Thus, we find:
TA=TB
Conclusion
The time periods of the two stars are equal:
TA=TB
We have two stars, A and B, with masses mA and mB respectively, moving in circular orbits of radii rA and rB. The time periods of these stars are TA and TB.
The center of mass (COM) of the system can be defined as:
mArA=mBrB
This equation indicates that the moments about the center of mass are equal. This is our Equation 1.
The gravitational force between the two stars provides the necessary centripetal force for their circular motion. The gravitational force Fg is given by:
Fg=GmAmB(rA+rB)2
The centripetal force for star A is:
FcA=mAV2ArA
And for star B:
FcB=mBV2BrB
Since the gravitational force provides the centripetal force, we can set up the following equations:
GmAmB(rA+rB)2=mAV2ArA(2)
GmAmB(rA+rB)2=mBV2BrB(3)
The velocities VA and VB can be expressed in terms of the time periods:
VA=2πrATA
VB=2πrBTB
Substituting VA and VB into equations (2) and (3):
GmAmB(rA+rB)2=mA(2πrATA)2rA
GmAmB(rA+rB)2=mB(2πrBTB)2rB
From the first equation:
GmAmB(rA+rB)2=4π2mArAT2A
From the second equation:
GmAmB(rA+rB)2=4π2mBrBT2B
Since both expressions are equal to the gravitational force, we can set them equal to each other:
4π2mArAT2A=4π2mBrBT2B
This simplifies to:
mArAT2A=mBrBT2B
From the center of mass condition mArA=mBrB, we can substitute rB=mAmBrA into the equation:
mArAT2A=mB(mAmBrA)T2B
This leads to:
1T2A=1T2B
Thus, we find:
TA=TB
The time periods of the two stars are equal:
TA=TB
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - MCQ_TYPE
4 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - AR_TYPE
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - True/False
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
Two satellites A and B of masses m1 and m2(m1=2m2) are moving in circular orbits of radii r1 and r2(r1=4r2), respectively, around the earth. If their periods are TA and TB, then the ratio TA/TB is
View SolutionTwo cars of mass m1andm2 are moving in circle of radii r1andr2 , respectively . Their speeds are such that they make complete circles in the same time t . The ratio of their centripetal acceleration is :
View SolutionTwo cars of mass m1andm2 are moving in circle of radii r1andr2 , respectively . Their speeds are such that they make complete circles in the same time t . The ratio of their centripetal acceleration is :
View SolutionTwo racing cars of masses m1 and m2 are moving in circles of radii r1 and r2 respectively. Their speeds are such that each makes a complete circle in the same time t. The ratio of the angular speed of the first to the second car is
View SolutionTwo particles of mass mA and mB and their velocities are VA and VB respectively collides. After collision they interchanges their velocities, then ratio of mAmB is
View SolutionTwo cars of masses m1 andm2 are moving in circles od radii r1andr2. Their speeds are such that they complete one revolution in the same time. The ratio of their angular speed is :
View SolutionTwo particles A and B are moving in uniform circular motion in concentric circles of radii rA and rB with speed uA and uB respectively. Their time period of rotation is the same. The ratio of angular speed of a to that of B will be:
View SolutionTwo cars having masses m1andm2 move in circles of radii r1andr2 respectively. If they complete the circle is equal time the ratio of their angular speeds is ω1ω2 is
View SolutionA planet of mass M, has two natural satellites with masses m1 and m2. The radii of their circular orbits are R1 and R2 respectively. Ignore the gravitational force between the satellites. Define v1,L1,K1 and T1 to be, respectively, the orbital speed, angular momentum, kinetic energy and time period of revolution of satellite 1 , and v2,L2,K2 and T2 to be he corresponding quantities of satellite 2. Given m1/m2=2 and R1/R2=1/4, match the ratios in List-I to the numbers in List-II.
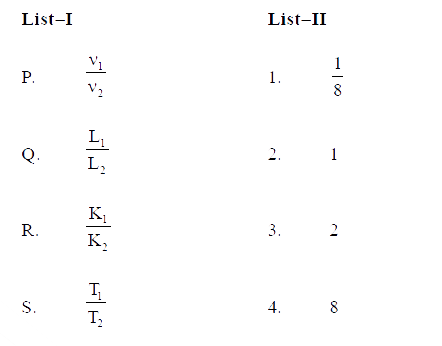
View SolutionTwo particles having mass 'M' and 'm' are moving in a circular path having radius R & r respectively. If their time period are same then the ratio of angular velocity will be : -
View Solution
