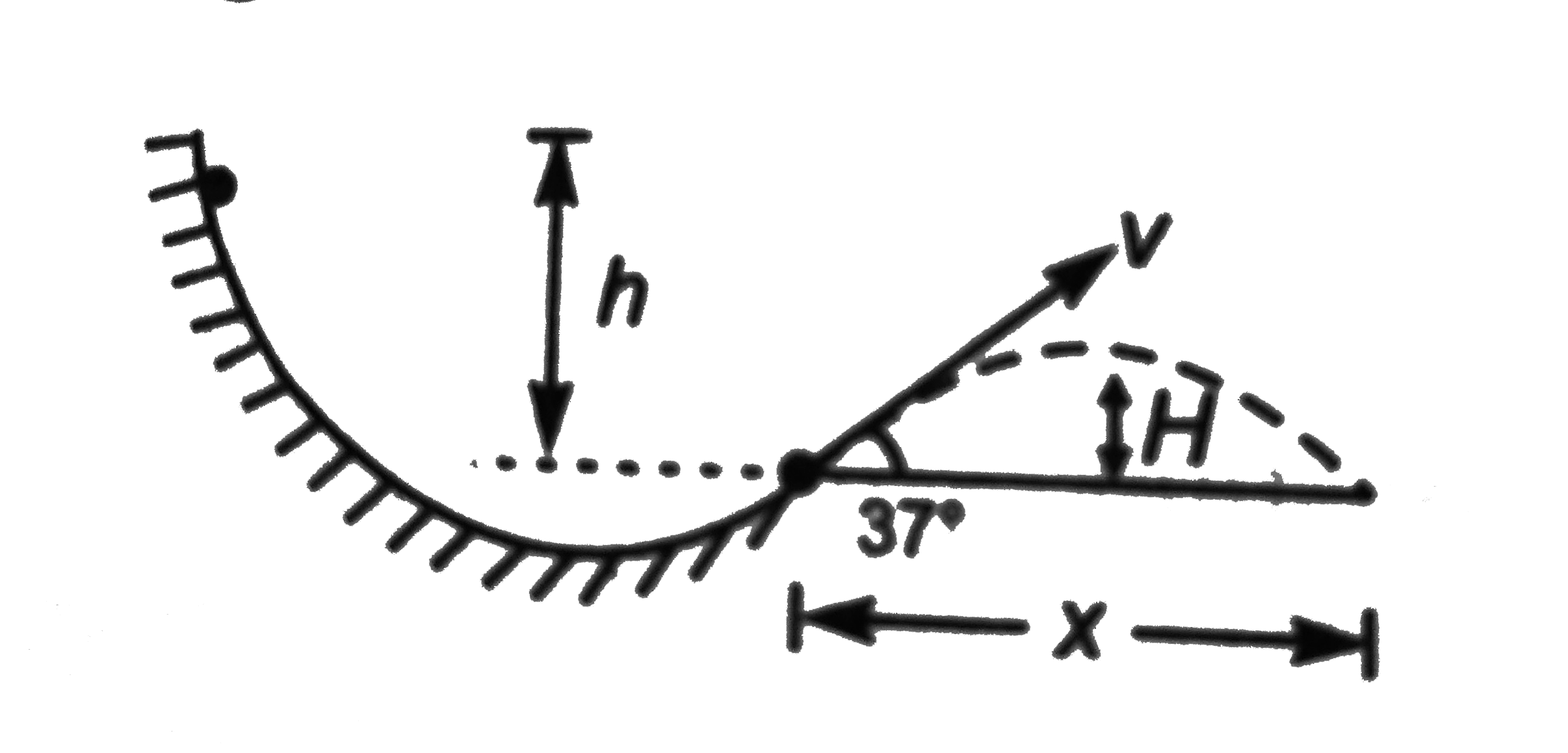
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. The velocity of projection v is
√2gh
√107gh
√57gh
√65gh
Ktotal after falling a height h is mgh
KRKT=23
∴KT=12mv2=(35)(mgh)
∴v=√6gh5
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Subjective
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
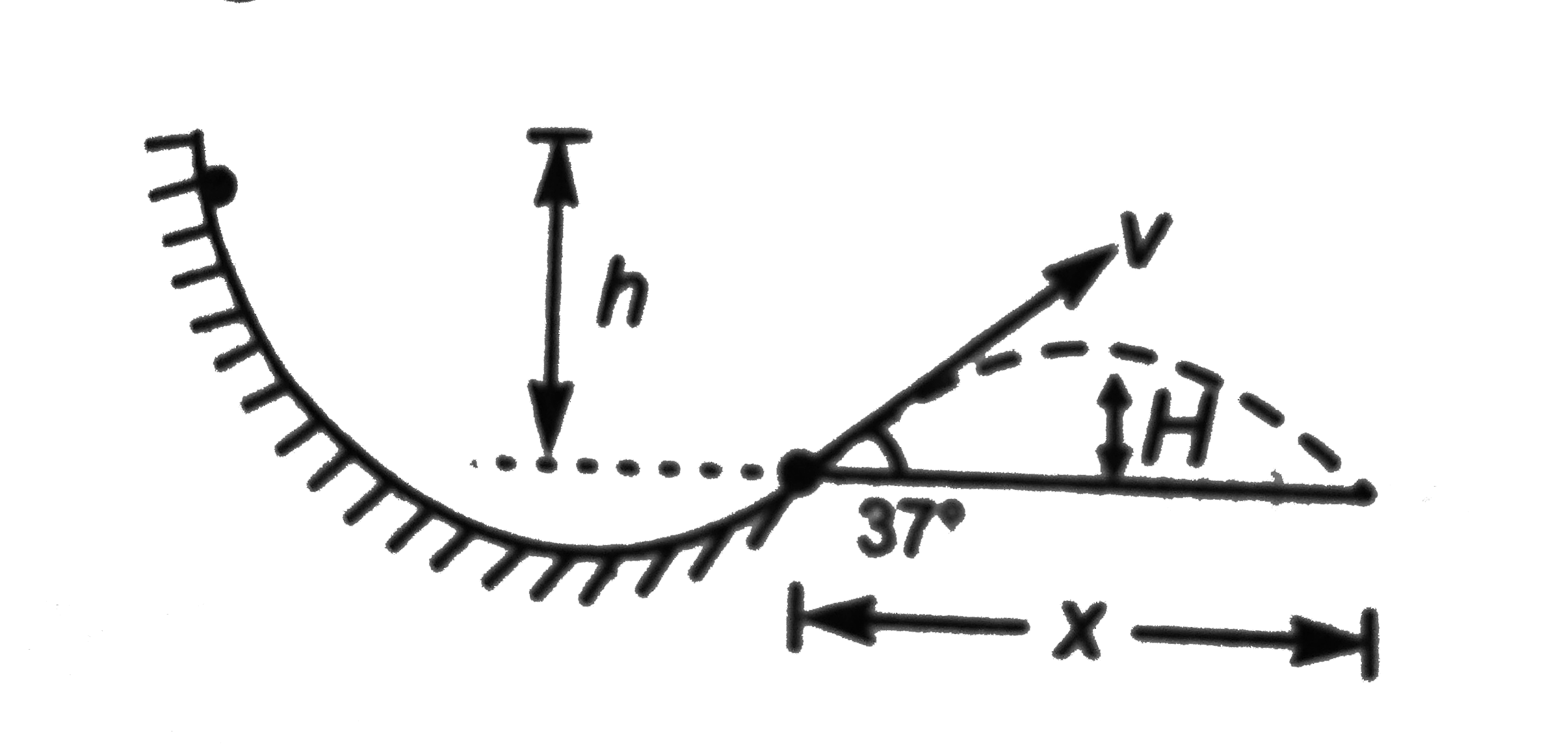
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Range x of the ball is
View Solution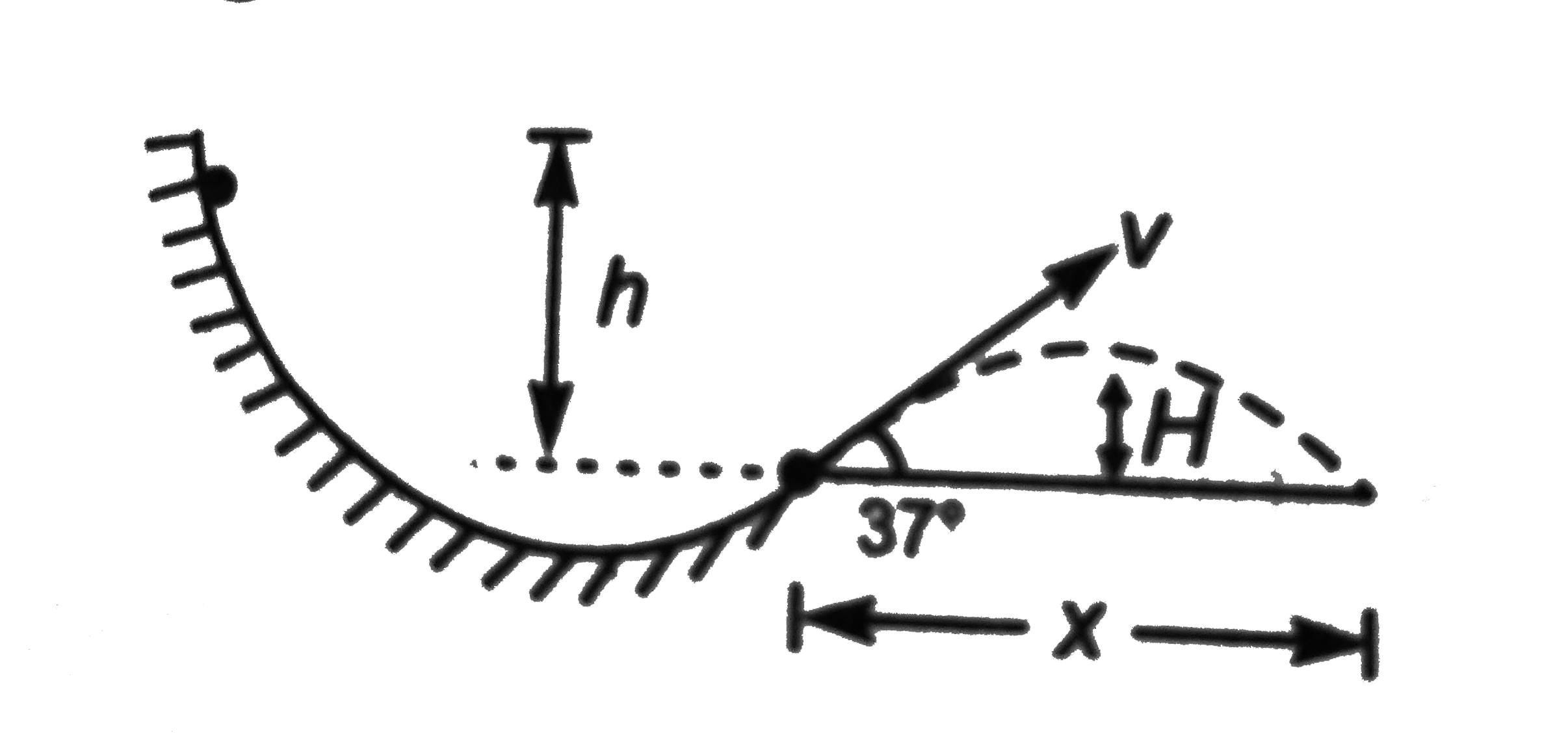
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Maximum height reached by ball H above ground is
View SolutionA ball is projected horizontal from the top of a tower with a velocity v0. It will be moving at an angle of 60∘ with the horizontal after time.
View SolutionA ball is projected from the ground at angle θ with the horizontal. After 1s, it is moving at angle 45∘ with the horizontal and after 2s it is moving horizontally. What is the velocity of projection of the ball ?
View SolutionAn elastic ball of mass 'm' is suspended from a fixed point by an inextensible string. A small particle of same mass m, moving downwards at an angle of 37∘ with the vertical lits the ball directly with the velocity v0. If the coefficient of restitution is 4/5,
(i) find the velocity of the ball just after the impact.
(ii) determine the impulsive tension(i.e impulse) in the string at the instant of collision.
View SolutionA ball was thrown by a boy a at angle 60∘ with horizontal at height 1 m from ground. Boy B is running in the plane of motion of ball and catches the ball at height 1 m from ground. He finds the ball falling vertically. If the boy is running at a speed 20 km/hr. Then the velocity of projection of ball is-
View SolutionFrom the the top of a tower 19.6 m high, a ball is thrown horizontally. If the line joining the point of projection to the point where it hits the ground makes an angle of 45∘ with the horizontal, then the initial velocity of the ball is:-
View SolutionA ball is thrown horizontally from a cliff such that it strikes the ground after 5s.The line of sight makes an angle 37∘ with the horizontal.The initial velocity of projection in ms−1 is
View SolutionA ball is thrown from the top of a tower with an intial velocity of 10 m//s at an angle 37∘ above the horizontal, hits the ground at a distance 16 m from the base of tower. Calculate height of tower. [g=10m/s2]
View SolutionA ball is projected horizontally from the top of a building 19.6 m high. If the line joining the point of projection to the point where it hits the ground makes an angle of 45∘ to the horizontal, the initial velocity of the ball is
View Solution
