
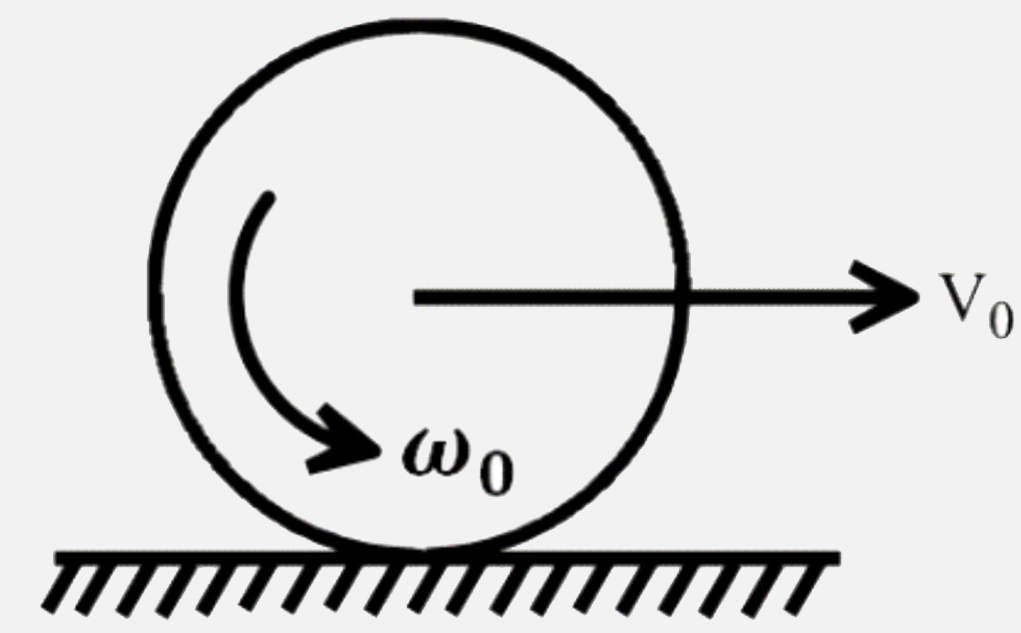
A disc of radius R is spun to an angualr speed ω0 about its axis and then imparted a horizontal velocity of magnitude ω0R4. The coefficient of friction is μ. The sense of rotation and direction of linear velocity are shown in the figure. The disc will return to its initial position.
if the value of μ<0.5
irrespective of the value of μ
if the value of 0.5<μ<1
if μ>1

About bottommost point
angular momentum
L=ICω0−mv0R (anticlockwise)
=12mR2ω−m(ω0R4)R

=14mR2ω0
=+ ve or anticlockwise
during slip friction acts about bottommost point. So, its torque is zero or angular momentum about bottommost point should also remain anticlockwise when pure rolling starts. so, figure should be as shown below.
so, the disc will return to its initial position for all value of μ.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Subjective
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A disc of the radius R is spun to an angular speed ω0 about its axis and then imparted a horizontal velocity of magnitude (at t = 0) with its plane remaining vertical. The coefficient of friction between the disc and the plane is μ . The sense of rotation and direction of its linear speed are shown in the figure . Choose the correct statement.
View SolutionA disc of radius R is spun to an angular speed ω0 about its axis and then imparted a horizontal velocity of magnitude ω0R4 (at t=0) with its plane remaining vertical. The coefficient of friction between the disc and the plane is μ. The sense of rotation and direction of its linear speed are shown in the figure. The disc returns to its initial point in time T=256kμgω0R. Find the value of k.
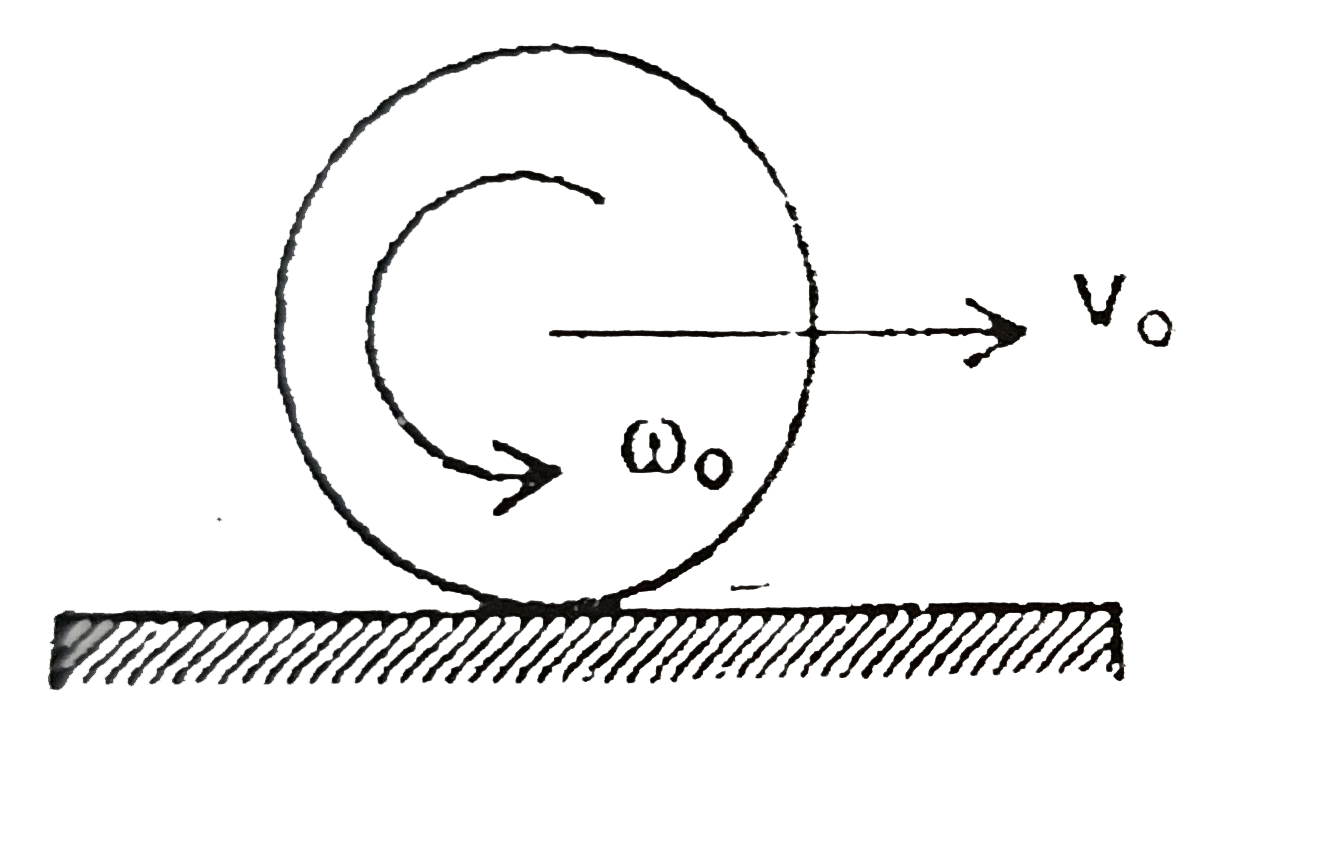
View Solution
Knowledge Check
A ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
AωoμkR2gBωog2μkRC2ωoRμkgDωoR2μkg
A disc of radius R is rotating with an angular ω0 about a horizontal axis it is placed on a horizontal table . The coefficient of kinetic friction is μk
(a) what was the velocity of its centre of mass before being brought in contact with a the table ?
(B) what happens to the linear velocity of a point on its rim when placed in contact with the table ?
(c ) what happes to the linear speed of the centre of mass when disc is placed in contact with the table ?
(d) which force is responsible for the effects in (b) and (C ) ?
(e) wht condition should be sattisfied for rolling to begin ?
(f) Calculate the time taken for the rolling to begin .
View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:
View SolutionA disc is given an initial angular velocity ω0 and placed on a rough horizontal surface as shown Fig. The quantities which will not depend on the coefficient of friction is/are

View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View Solution
solid sphere of radius r is gently placed on a rough horizontal ground with an initial angular speed ω0 and no linear velocity. If the coefficient of friction is μ, find the time t when the slipping stops. in addition state the linear velocity v and angular velocity ω at the end of slipping
View Solution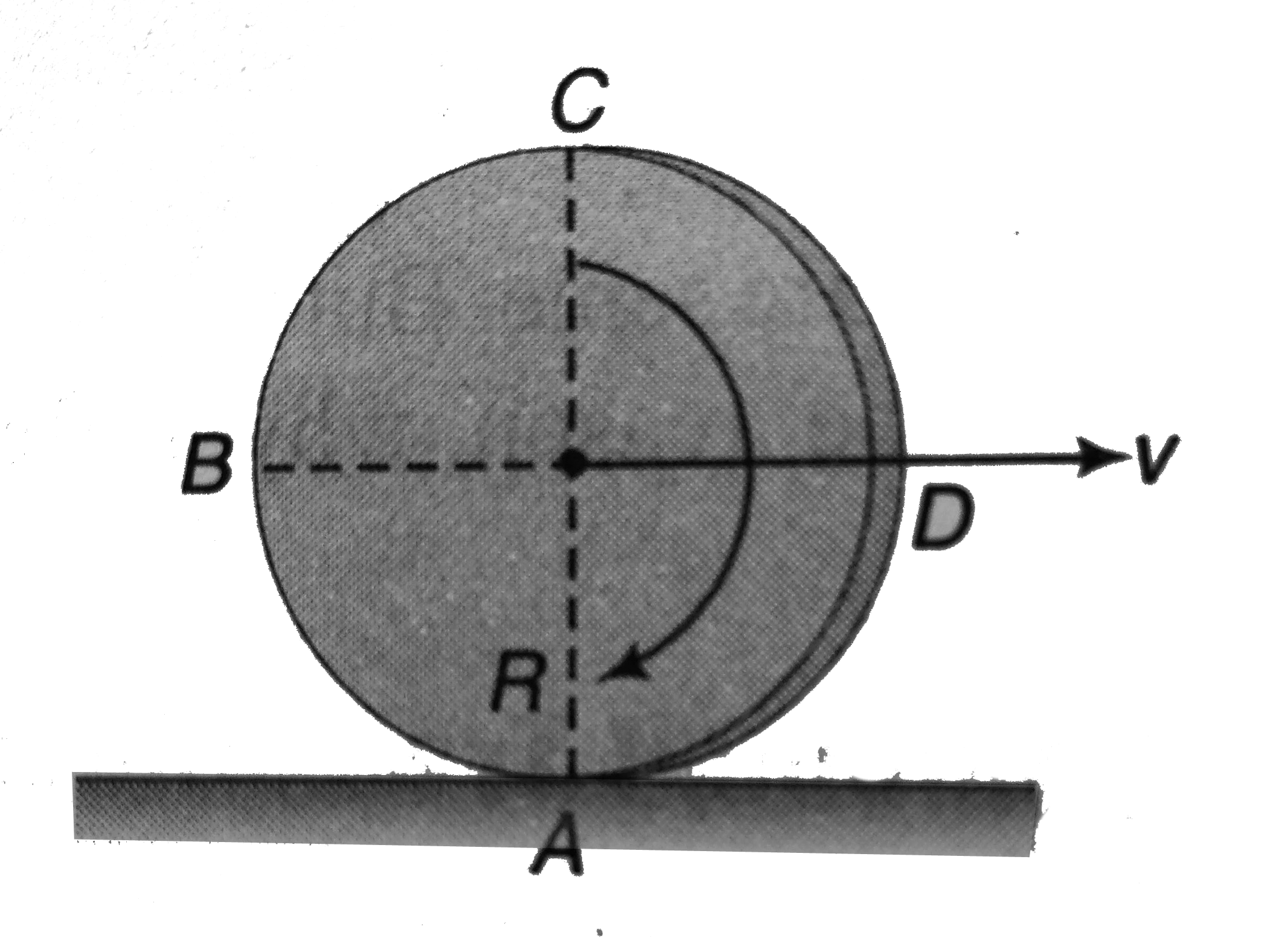
A disc of radius R has linear velocity v and angular velocity ω as shown in the figure. Given υ=rω find velocity of point A, B, C and D on the disc.
View SolutionFind the position of instantaneous centre of rotation and angular velocity of the disc in the following cases as shown. Radius of disc is R in each case.

View Solution
