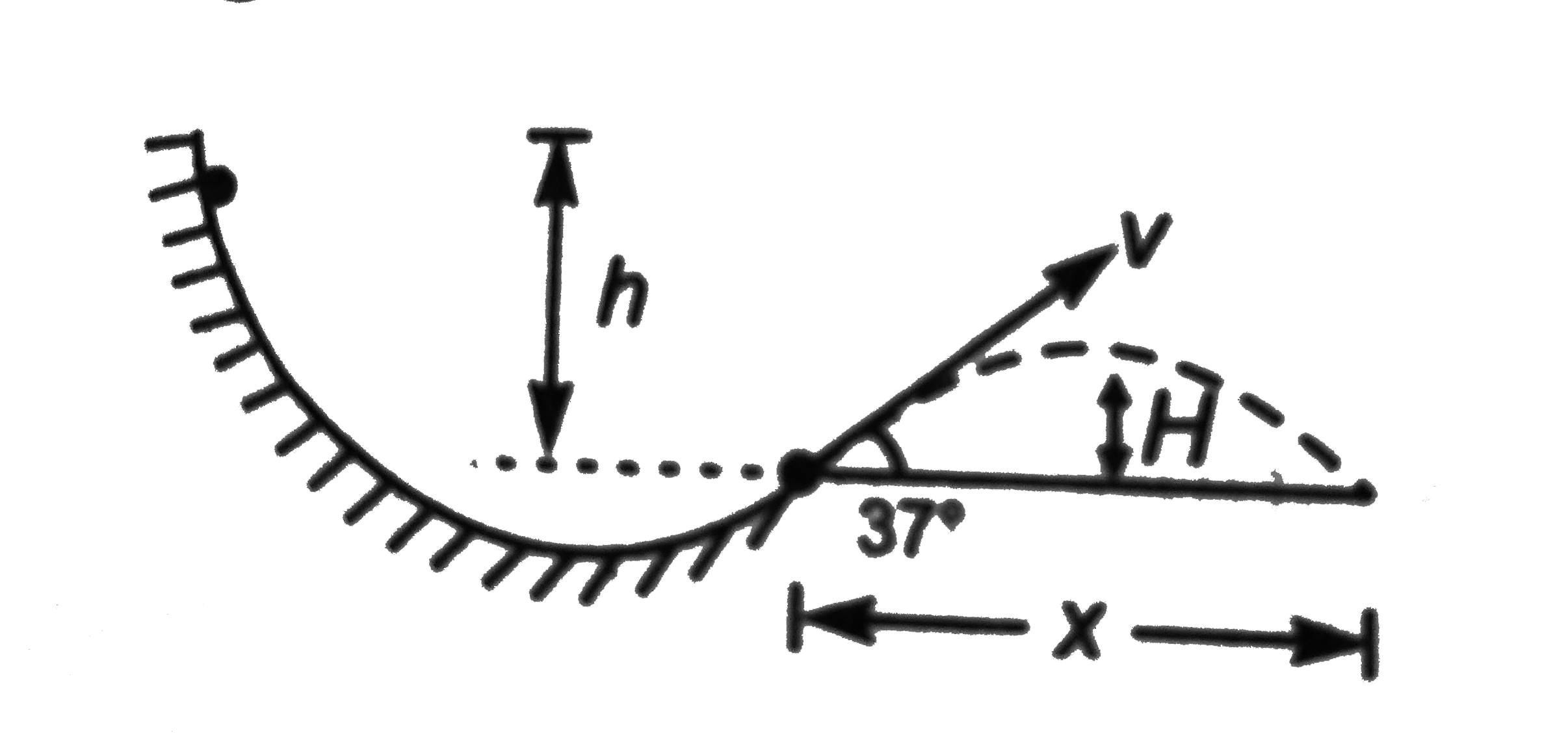
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Maximum height reached by ball H above ground is
9h35
18h35
18h25
27h125
H=v2sin2sin37∘2g
=(6gh/5)(3/5)22g=27h125
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2
Explore 1 Video
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2 Subjective
Explore 36 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2 Single Correct
Explore 26 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
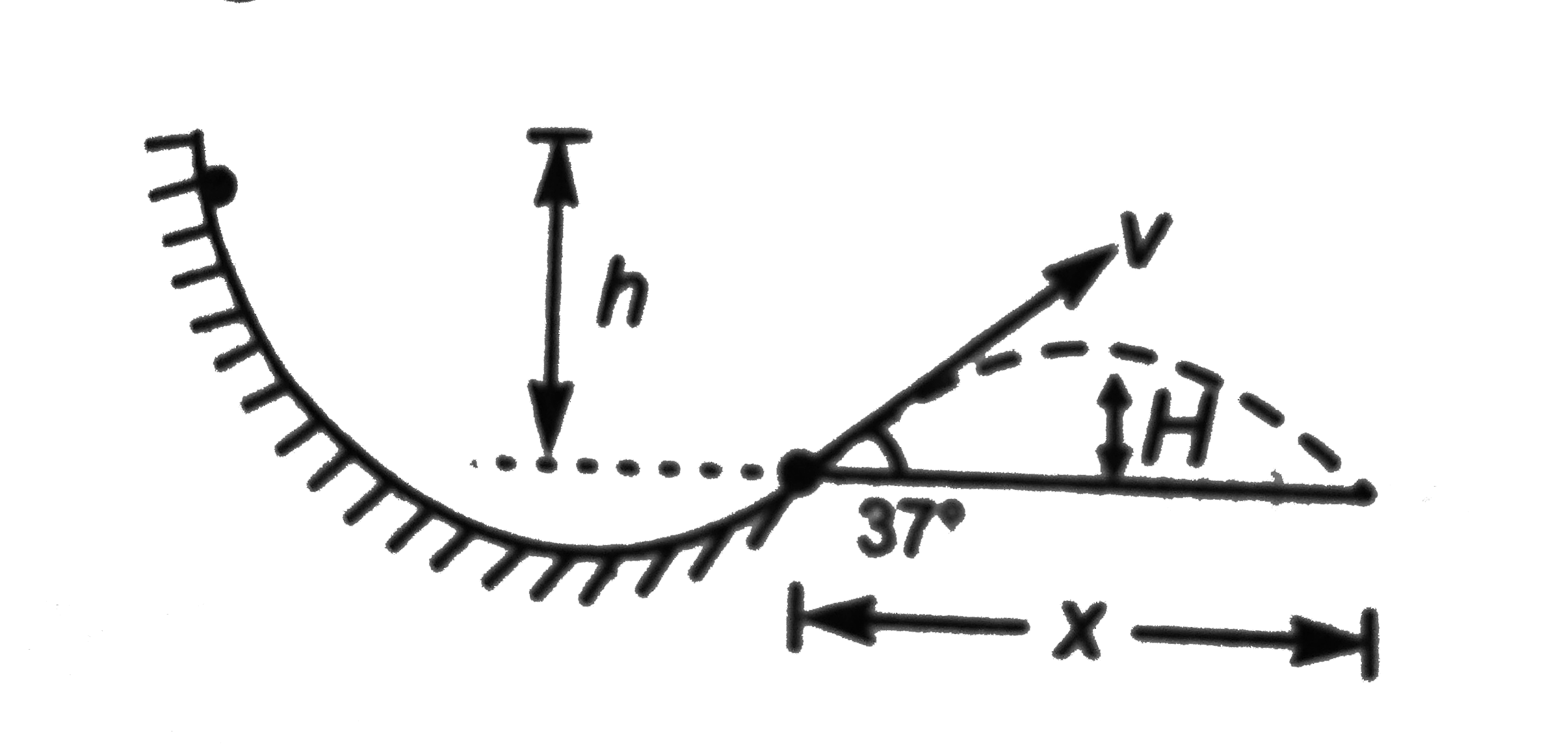
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Range x of the ball is
View Solution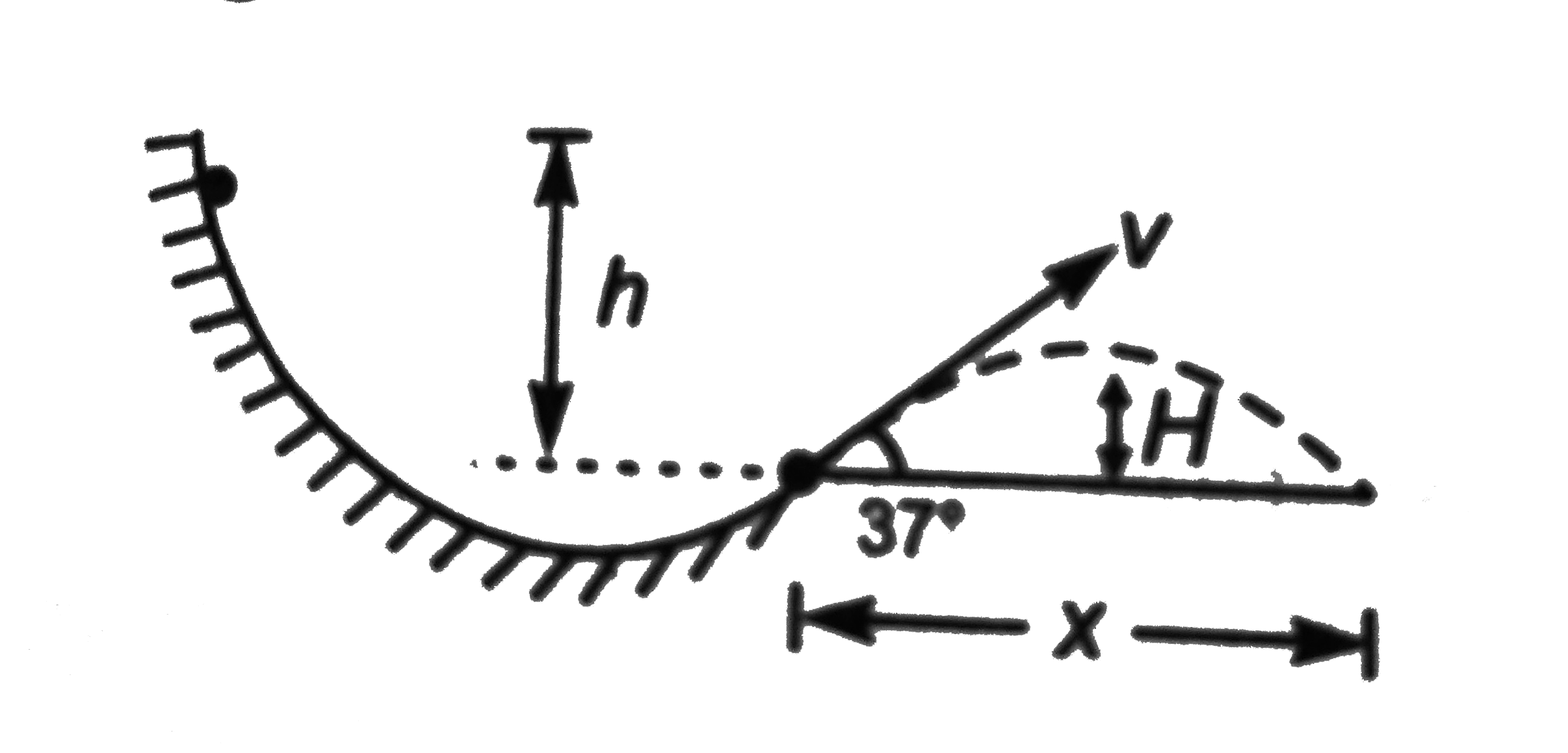
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. The velocity of projection v is
View SolutionA small ball of mass m is thrown upward with velocity u from the ground. The ball experiences a resistive force mkv2 where v is its speed. The maximum height attained by the ball is :
View SolutionAn elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
2. The maximum height reached by ball, as measured from the ground would be
View SolutionA ball is drpped from rest at height 4h. After it has fallen a distance d, a second ball is dropped from rest at height h. What should d be (in terms of h) so that the balls hit the ground at the same time?
View SolutionA ball is thrown from the top of a building 45m high with a speed 20ms−1 above the horizontal at an angle of 30∘. Find
(a) The time taken by the ball to reach the ground.
(b) The speed of ball just before it touches the ground.
View SolutionA man in a balloon rising vertically with acceleration 4.9m/s2 of releases a ball 2 sec after the balloon is let go from the ground. The greatest height above ground reached by the ball is : (g=9.8m/s2)
View SolutionA ball is released from point A as shown in figure. The ball leaves the track at B. All surfaces are smooth.

If track makes an angle 30∘ with horizontal at B, then maximum height attained by ball will be
View SolutionThe height h , in feet , of a ball shot upward from a ground level spring gun is described by the formula h=−16t2+48t. Where t is the time in seconds. What is the maximum height , in feet , reached by the ball ?
View SolutionA ball is thrown from the top of a 35m high tower with initial velocity of magnitude u=80 ms−1 at an angle 25∘ with horizontal.
Find the time to reach the ground and the horizontal distance covered by the ball.
View Solution
