A tennis ball with (small) mass m2 rests on the top of a basketball of mass m1which is at a height h above the ground, and the bottom of the tennis ball is at height h+d above the ground. The balls are dropped. To what height does the tennis ball bounce with respect to ground? (Assume all collisions to be elastic and m1>>m2)
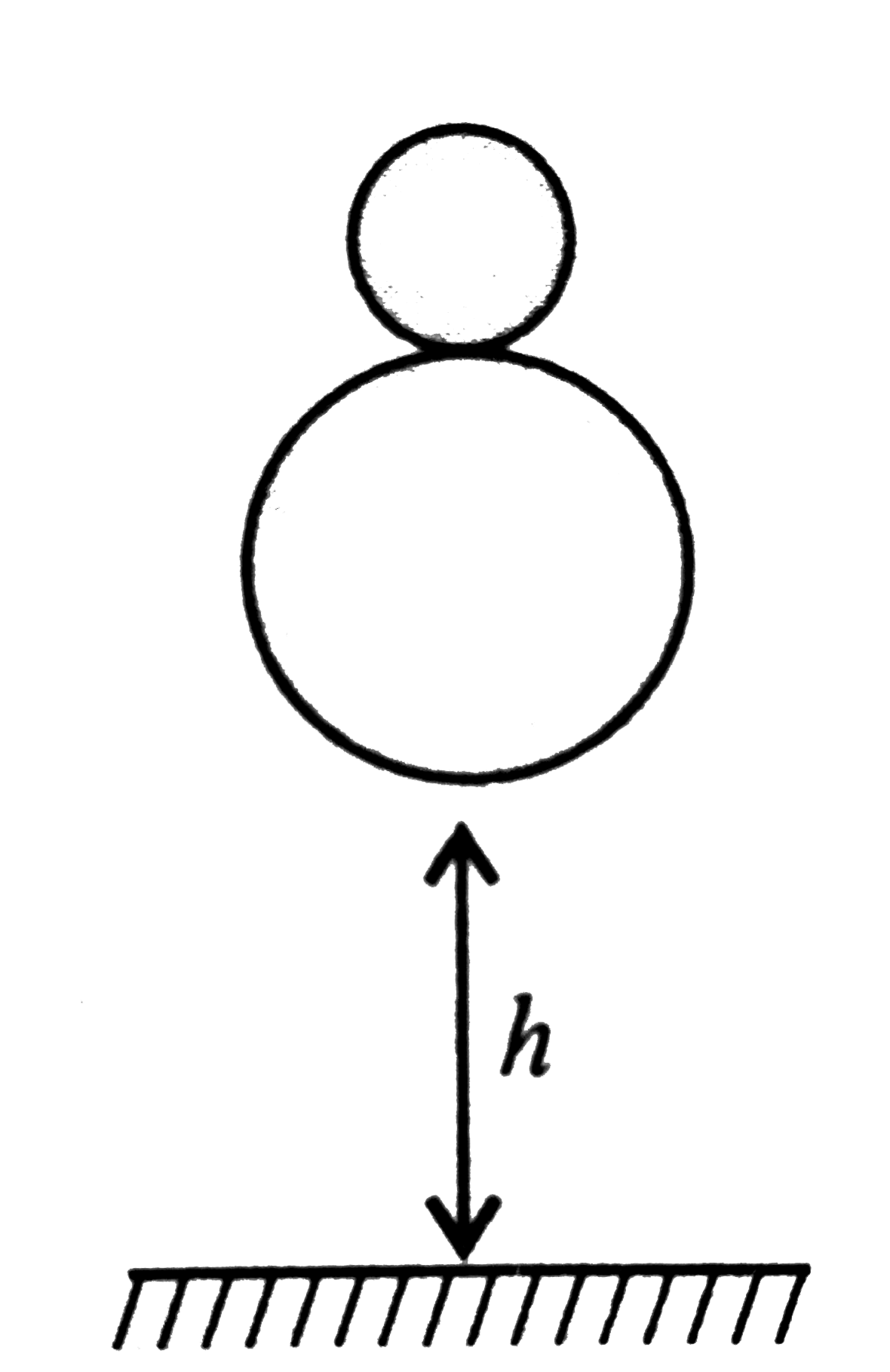
The correct Answer is:d+9h
Just before collision speed of any ball,
v=√2gh
Just after collision m1 moves up with v while m2 moves down with v.
After the collision e=v'−vv−(−v)=1
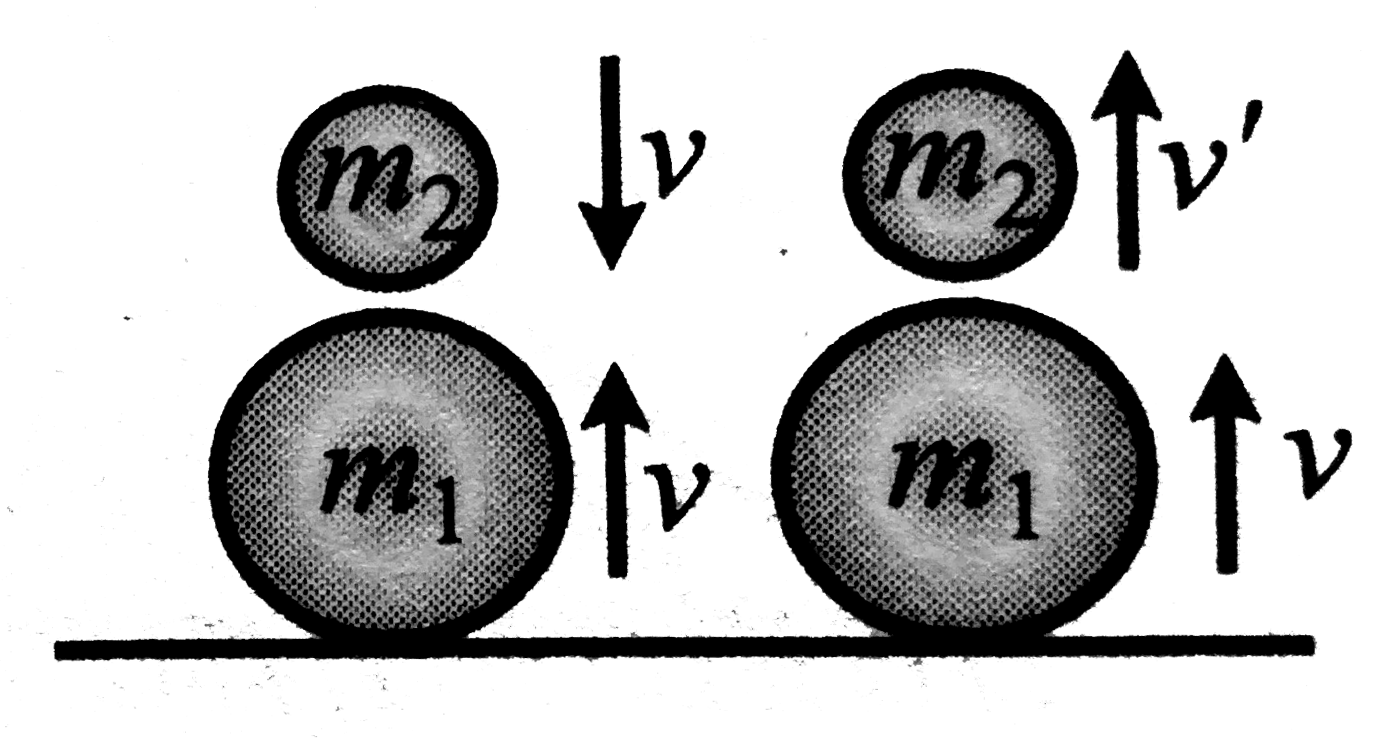
⇒v'=3v
02=(3v)2−2gh'
⇒h'=9v22g⇒H=d+9v22g=d+9h
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.3
24 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions

A small ball of mass m2 rests on the top of a bigger ball of mass m1(>>m2. The centre of bigger ball is at height 3r above ground as shown. The balls are dropped from this situation. If the smaller ball bounces to a height 4 nr from ground after its first collision with bigger ball. find n. (Assume all collisions are elastic).
View SolutionA ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
View Solution
Knowledge Check
A ball is dropped from a height h on the ground If the coefficient of restitution is e, the height to which the ball goes up after it rebounds for the nth time is
Ahe2nBhenCe2nhDhe2nA wooden ball and an iron ball are dropped from the same height h in vaccum. If their radii are the same then the time taken by then to reach the ground are
Aapproximately equalBexactly equalCnot equalDzero
A ball is dropped from a height h above ground. Neglect the air resistance, its velocity (v) varies with its height (y) above the ground as :-
View SolutionA ball dropped from a height of 2 m rebounds to a height of 1.5 m after hitting the ground. Then fraction of energy lost is
View SolutionA ball is projected upwards from a height h above the surface of the earth with velocity v. The time at which the ball strikes the ground is
View SolutionA ball is projected upwards from a height h above the surface of the earth with velocity v. The time at which the ball strikes the ground is
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View SolutionIn a gravity free space, man of mass M standing at a height h above the floor, throws a ball of mass m straight down with a speed u. When the ball reaches the floor, the distance of the man above the floor will be.
View Solution
