A small bucket of mass M is attached to a long inextensible cord of length L. The bucket is released from rest when the cord is in a horizontal position. In its lowest position the bucket scoops up m of water, what is the height of the swing above the lowest position?
The correct Answer is:l
To solve the problem step by step, we will use the principles of conservation of energy and momentum.
Step 1: Determine the velocity of the bucket at the lowest position
When the bucket is released from the horizontal position, it falls under the influence of gravity. We can use the work-energy theorem to find the velocity of the bucket at the lowest position.
The work done by gravity when the bucket falls a distance L is equal to the change in kinetic energy. Since the bucket starts from rest, the initial kinetic energy is zero.
Work done by gravity=ΔKE=KEfinal−KEinitial
mgh=12mv2
Here, h=L (the height fallen), and g is the acceleration due to gravity. Thus, we have:
mgL=12mv2
Cancelling m from both sides (assuming m≠0), we get:
gL=12v2
Rearranging gives:
v2=2gL
Taking the square root:
v=√2gL
Step 2: Calculate the velocity after scooping up water
When the bucket scoops up m mass of water, we need to find the new velocity v′ of the bucket. By conservation of momentum:
Initial momentum=Final momentum
Before scooping, the momentum is:
Mv
After scooping, the momentum is:
(M+m)v′
Setting these equal gives:
Mv=(M+m)v′
Solving for v′:
v′=MvM+m
Substituting v=√2gL:
v′=M√2gLM+m
Step 3: Determine the height h above the lowest position
Now, we will apply the work-energy theorem again to find the height h the bucket rises after scooping the water. The work done by gravity as the bucket moves up is equal to the change in kinetic energy.
Work done by gravity=−mgh=ΔKE=12(M+m)v′2−0
Substituting for v′:
−mgh=12(M+m)(M√2gLM+m)2
Simplifying the right side:
−mgh=12(M+m)⋅M2⋅2gL(M+m)2
Cancelling (M+m) from both sides:
−mgh=M2gL(M+m)
Now, rearranging for h:
h=M2L(M+m)
Final Answer
The height of the swing above the lowest position is:
h=M2L(M+m)
---
When the bucket is released from the horizontal position, it falls under the influence of gravity. We can use the work-energy theorem to find the velocity of the bucket at the lowest position.
mgh=12mv2
When the bucket scoops up m mass of water, we need to find the new velocity v′ of the bucket. By conservation of momentum:
Now, we will apply the work-energy theorem again to find the height h the bucket rises after scooping the water. The work done by gravity as the bucket moves up is equal to the change in kinetic energy.
The height of the swing above the lowest position is:
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.3
24 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
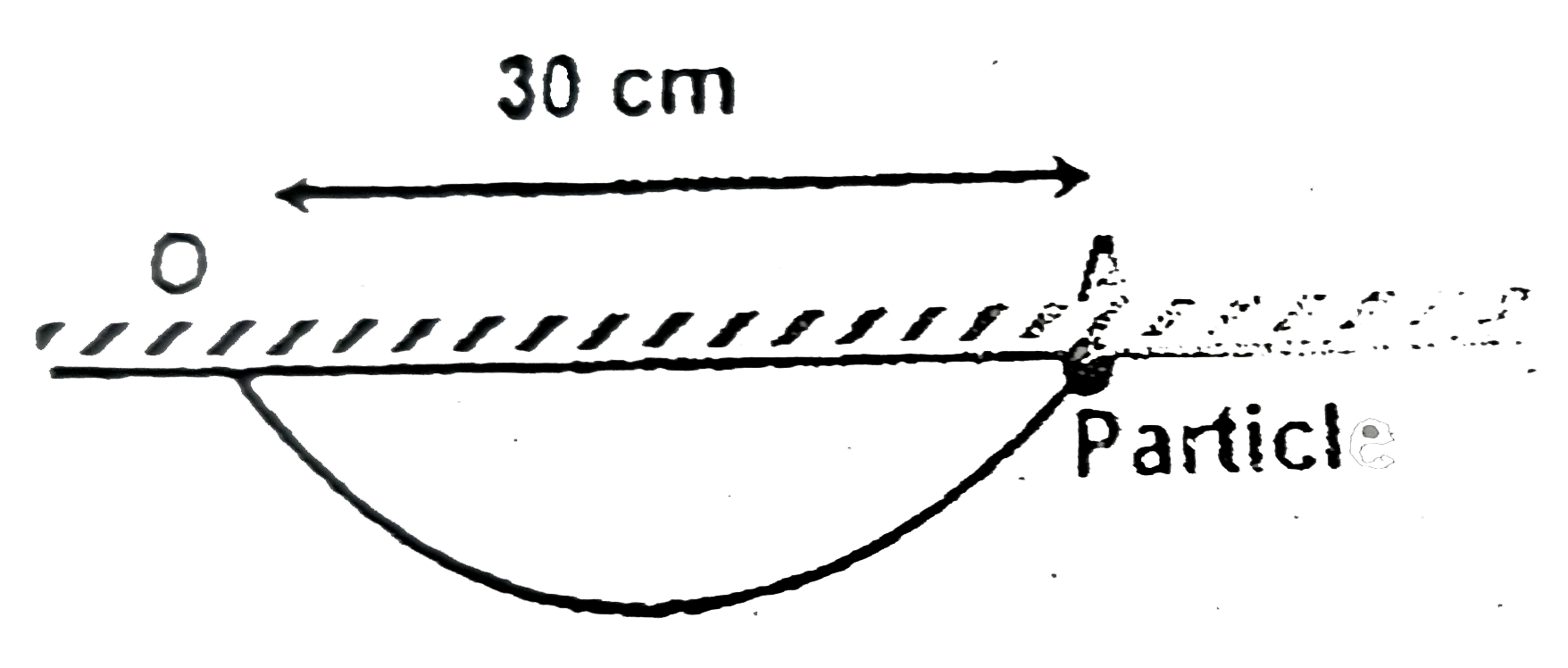
A small ball of mass 100g is attached to a light and inextensible string of length 50cm. The string is tied to a support O and the mass m released from point A which is a' a horizontal distance of 30cm from the support. Calculate the speed of the ball is its lowest point of the trajectory.
View SolutionA bob of mass m is connected by string of length L to point P. The system is released from rest with the pendulum bob in a horizontal position. Which of the following graph is correctly showing the variation of T (tension) with Ɵ?
View SolutionA bob hangs from a rigid support by an inextensible string of length l. It is released from rest when string makes an agngle 60∘ with vertical . The speed of the bob at the lowest position is
View SolutionA uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
View SolutionA particle of mass m attached with a massless spring natural length l and stiffness k is released from rest from the horizontal position of the relaxed spring. When the particle passes through its lowest point, the maximum length of the spring becomes 2l. Find the:
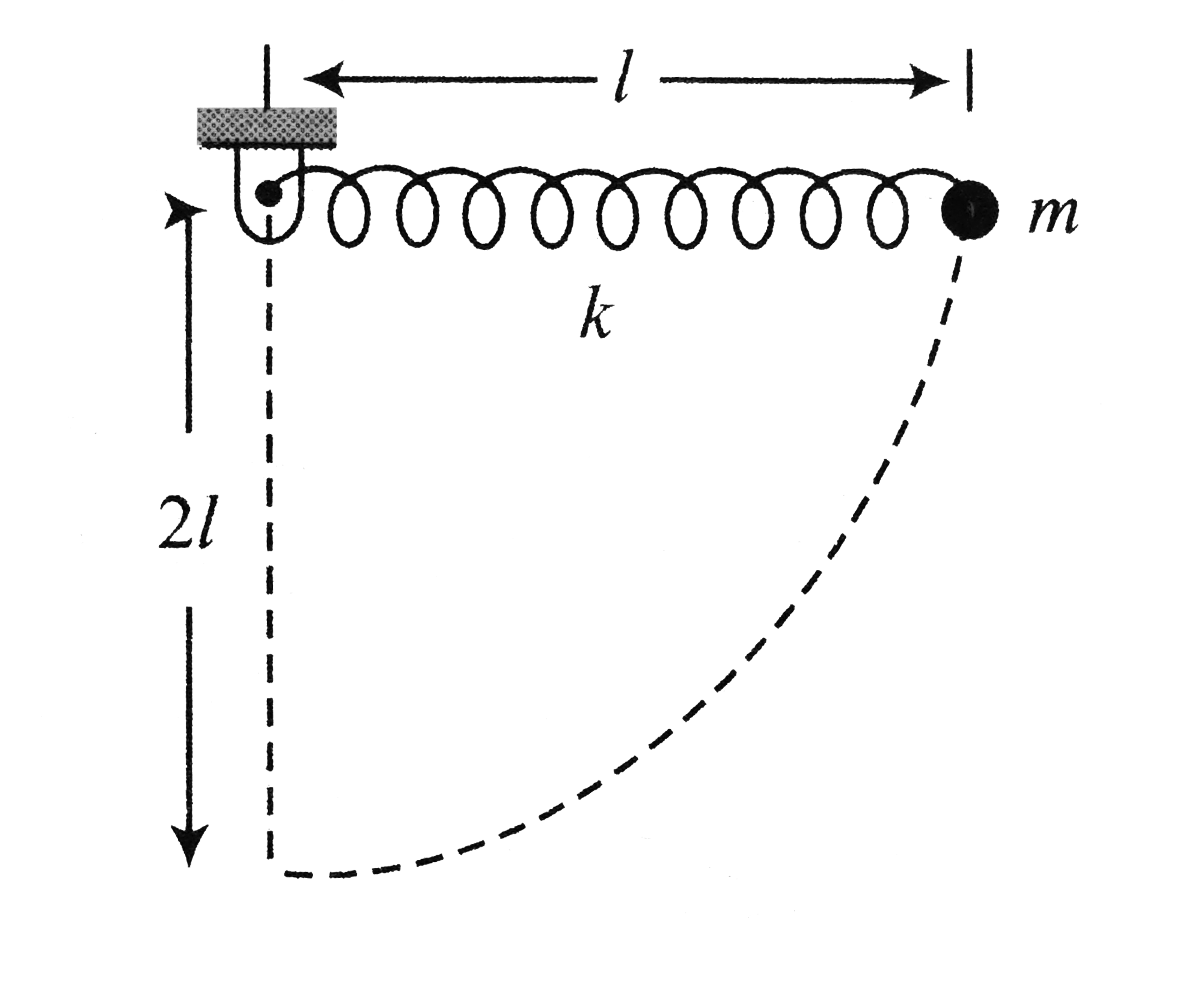
a. speed of the particle at its lowest point.
b. acceleration of the particle at its lowest position.
View SolutionThe string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View SolutionA partical of mass m attached with a massless spring of natural length l and stiffness constant k is releaased from rest from the horizontal positon of the relaxed spring.

When the particle passes through its lowest point, the maximum length of the spring bocomes 2l find the
(A) Speed of the particle at its lowest point
(B) Acceleration of the particle at its lowest position.
View SolutionA bob hangs from a rigid support by an inextensible string of length l. If it is displaced through a distance l (from the lowest position) keeping the string straight and then released. The speed of the bob at the lowest position is

View SolutionA rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position, is
View SolutionA particle of mass m is attached to a string of length L and given velocity √10gL in the horizontal direction at the lowest point. Find tension in the string when the particle is at (i) lowest position (ii) highest position,
View Solution
