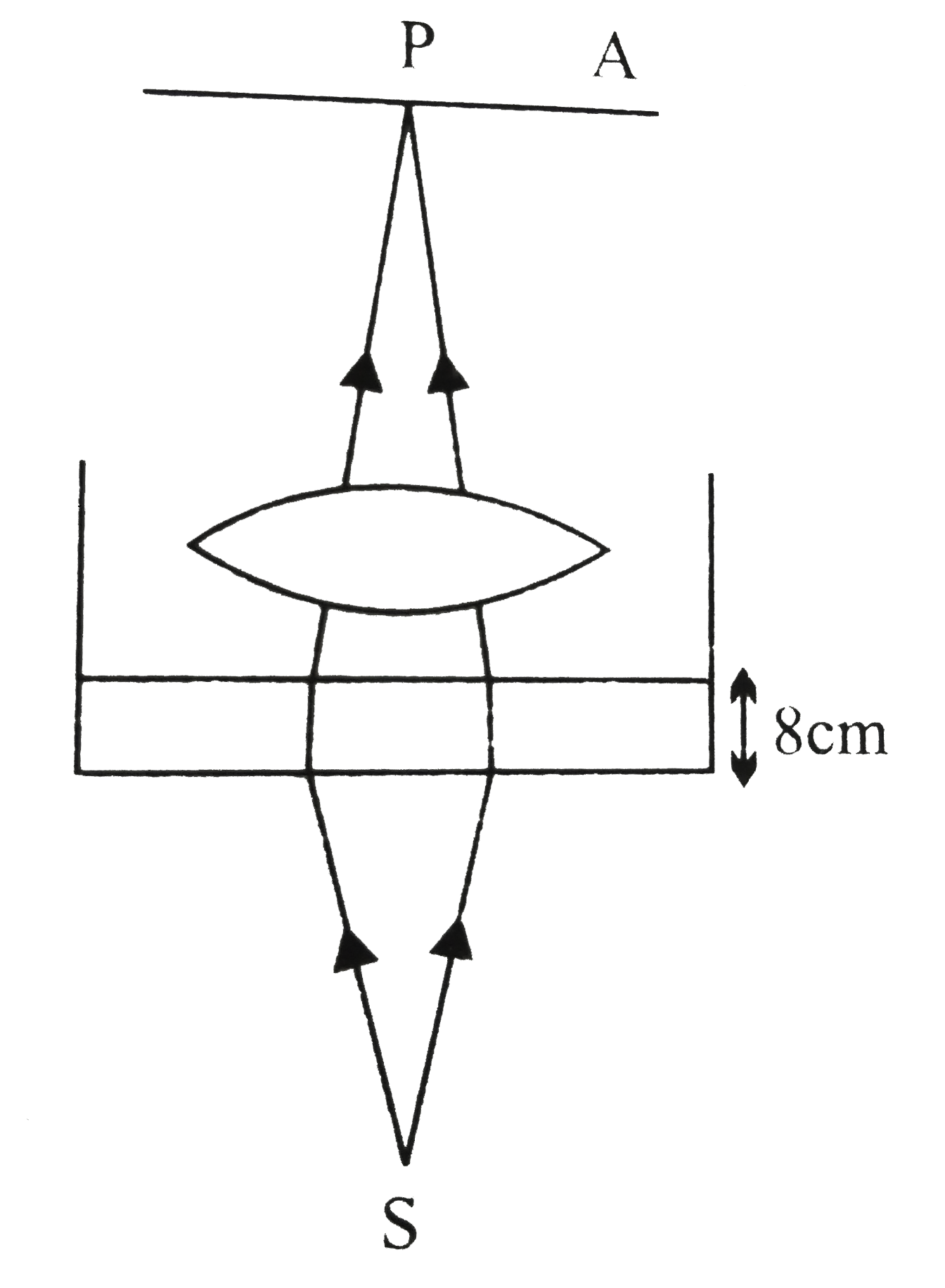
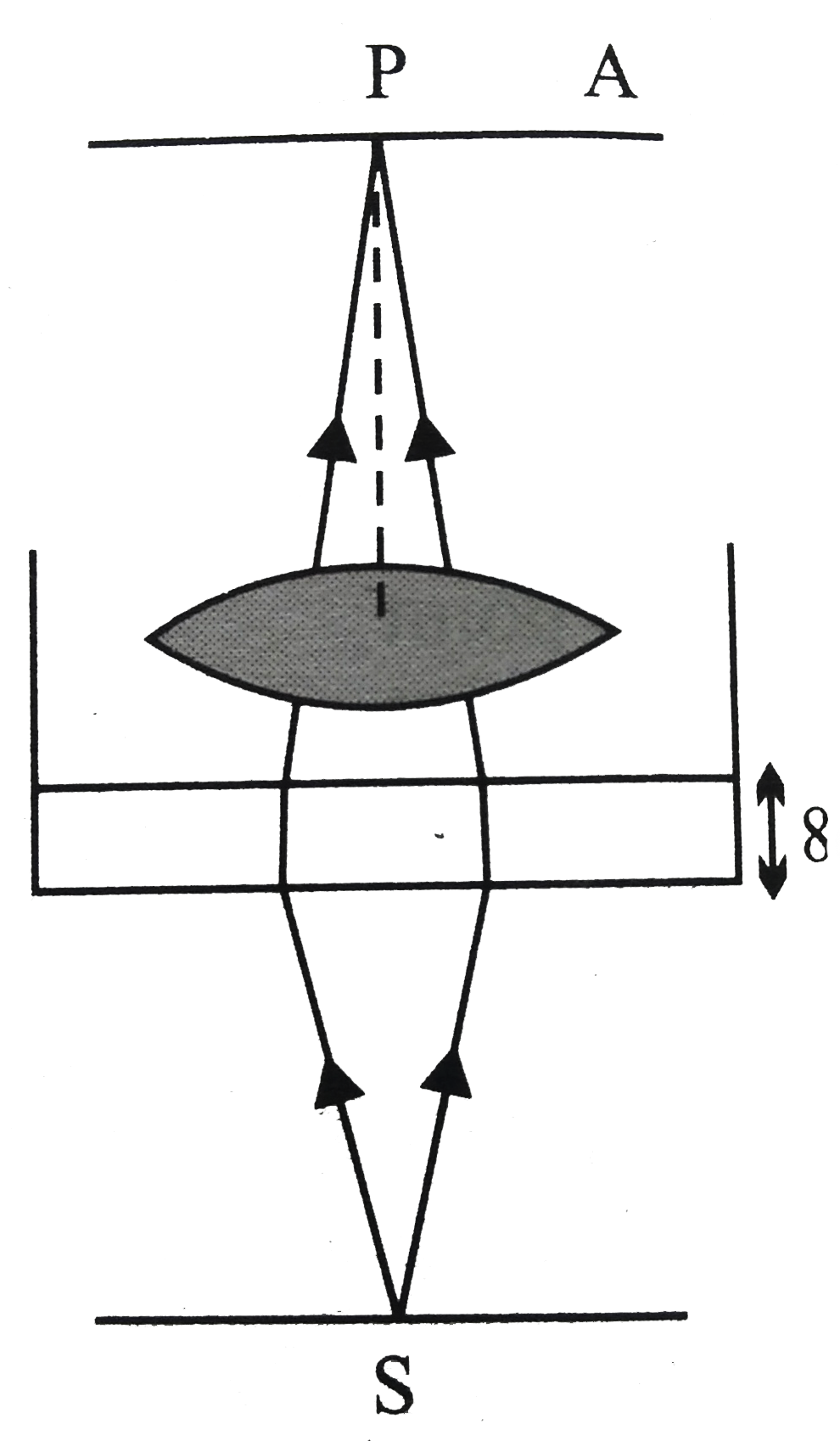
A thin convex lens of refractive index μ=1.5 is placed between a point source of Light S and a screen A, shown in figure,. Light rays from the source S are brought to focus on the screen A, forming a point image P. The distance SP is equal to 50cm. Water (μ=4/3) is now poured into a vessel interposed between the object and the lens, and it is observed that when the water level is 8cm the screen has to be moved up by a distance of 6cm in order to get a sharp image. Find the focal length of the lens.
The correct Answer is:|u|=20cm
|v|=30cm and f=12cm
Suppose that the object distance (between the oject and the lens) be u and the image distance v. Then,
|u|+|v|=50
1|v|−1|u|=1f (i)
When water is poured into the vessel,
1(|v|+6)−1−(|u|−2)=1f (ii)
Solving the equation, we get
|u|=20cm
|v|=30cm and f=12cm
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Single Correct221videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.721videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
Knowledge Check
- Question 1 - Select One
A screen is placed 90cm from an object. The image of the object on the screen is formed by a convex lens at two different location separated by 20cm. Determine the focal length of the lens.
A42.8cmB21.4cmC10.7cmD5.5cm
A screen is placed 90 cm from an object. The image an object on the screen is formed by a convex lens two different locations separated by 20 cm. the focal length of the lens is
View SolutionA screen is placed a distance 40 cm away from an illuminated object. A converging lens is placed between the source and the screen and it is attempted to form the image of the source on the screen. If no position could be found, the focal length of the lens
View SolutionAn object is placed 30cm away from a convex lens of focal length 10cm and a sharp image is formed on a screen. Now, a convex lens is placed In contact with the convex lens. The screen now has to be moved by 45cm to get a sharp image again. The magnitude of focal length of the convex lends in (in cm)
View SolutionA bi-convex lens is placed between a light source and a concave mirror as shwon such that image of the light source coincides with itself. Then,
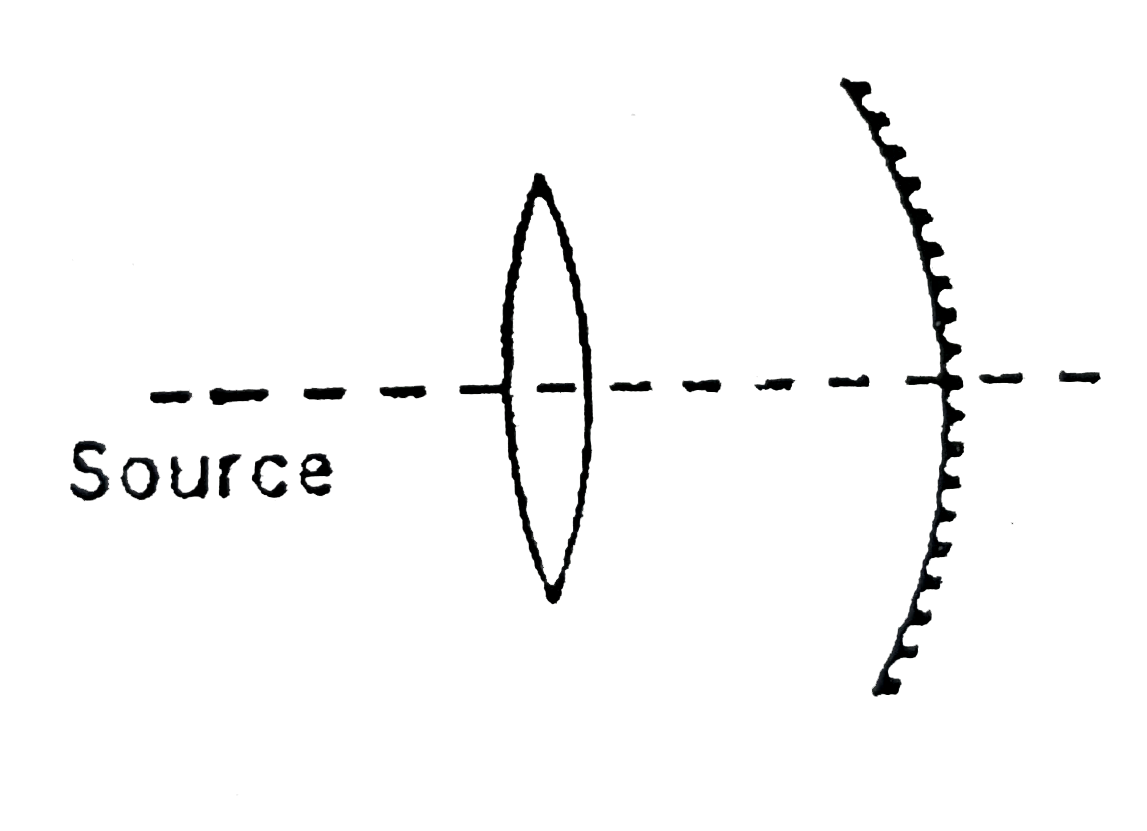 View Solution
View SolutionA convex lens forms an image of an object on a screen 30 cm from the lens. When the lens is moved 90 cm towards the object, then the image is again formed on the screen. Then, the focal length of the lens is
View SolutionThe diagram shows a point source of light S, a convex lens L and plane mirror M. These are placed such that rays of light from S return to it after reflection from M.
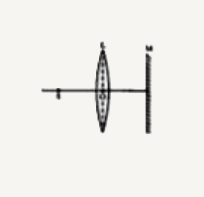
What is the distance OS called?View SolutionA convex lens of focal length f is placed somewhere in between an object and a screen. The distance between the object and the screen is x. If the numerical value of the magnification produced by the lens is m, then the focal lnegth oof the lens is .
View Solution