A thin hoop of mass M and radius r is placed on a horizontal plane. At the initial instant, the hoop is at rest. A small washer of mass m with zero initial velocity slides from the upper point of the hoop along a smooth groove in the inner surfaces of the hoop. Determine the velocity u of the centre of the hoop at the moment when the washer is at a certain point A of the hoop, whose radius vector forms an angle ϕ with the vertical (figure). The friction between the hoop and the plane should be neglected

The correct Answer is:B, C
Let vr be the velocity of washer relative to centre of hoop and v the velocity of centre of hoops. Applying conservation of linear momentum and mechanical energy we have,
m(vrcosϕ−v)=Mv …(i)
mgr(1+cosϕ)
=12Mv2+12m(v2r+v2−2vvrcosϕ) ...(ii)
Solving Eqs. (i) and (ii), we have,
v=mcosϕ
⎷2gr(1+cosϕ)(M+m)(M+sin2ϕ)
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Comprehension Based Questions
3 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A hoop of mass M and radius R is placed on an absolutely smooth level surface. An insect of mas m begins to alight along the hoop from the highest point with speed v relative to the hoop. Find the velocity of the centre of the hoop aftert.
View SolutionA hoop of radius R rests on a horizontal surface. A similar hoop moves past it at a velocity v. Determine the velocity vA of the upper point of "intersection" of the hoops as a function of the distance d between their centres, assuming that the hoops are thin, and the second hoop is in contact with the first hoop as it moves past the latter.
View Solution
Knowledge Check
A hoop of mass M and radius R is hung from a support fixed in a wall . Its moment of inertia about the support is
A2MR2B3MR2C4MR2D6MR2A hoop of mass 500gm & radius 10cm is placed on a nail, then the moment of inertia of the hoop, when it is rotated about the nail will be ____kgm2
A0.05B0.02C0.01D0.03A hoop of radius r and mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases ot slip?
Arω04Brω03Crω02Drω0
A hoop of radius r mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
View SolutionA circular hoop of mass m and radius R rests flat on a horizontal frictionless surface A bullet also of mass m and moving with a velocity v strikes the hoop and gets embedded in it the thickness of the hoop is much smaller then R the angular velocity with which the system rotates after the bullet strikes the hoop is

View SolutionA hoop rolls on a horizontal ground without slipping with linear speed v. Speed of a particle P on the circumference of the hoop at angle θ is :
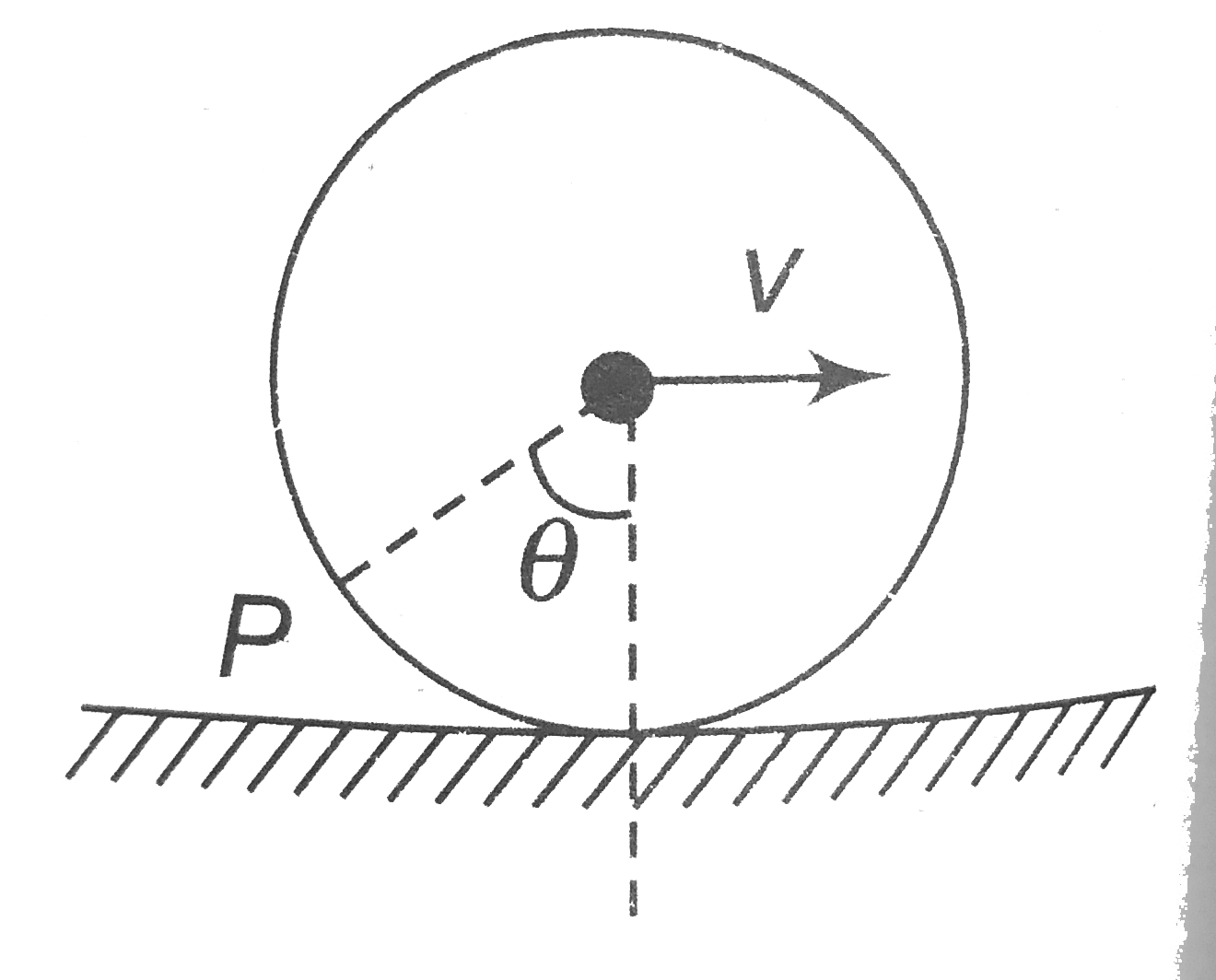
View SolutionA circular hoop of mass m and radius R rests flat on a horizontal smooth surface. A bullet of same mass m and moving with velocity υ strikes the hoop tangentially and gets embedded in it. Neglect the thickness of hoop in comparision to radius of hoop.

Velocity of CM of hoop (ground frame)is
View SolutionA block of mass m moves on a horizontal rough surface with initial velocity v. The height of the centre of mass of the block is h from the surface. Consider a point A on the surface.
View Solution
