(i) O is a fixed peg at a height H above a perfectly inelastic smooth horizontal plane. A light inextensible string of length L(>H) has one end attached to O and the other end is attached to a heavy particle. The particle is held at the level of O with string horizontal and just taut and released from rest. Find the height of the particle above the plane when it comes to rest for the first time after the release.

(ii) The bob of a pendulum has mass m and the length of pendulum is l. It is initially at rest with the string vertical and the point of suspension at a height 2l above the floor. A particle P of mass
m2 moving horizontally along –ve x-direction with velocity √2gl collides with the bob and comes to rest. The bob swings and when it comes to rest for the first time, another particle Q of mass m moving horizontally along y direction collides with the bob and sticks to it. It is observed that the bob now moves in a horizontal circle.
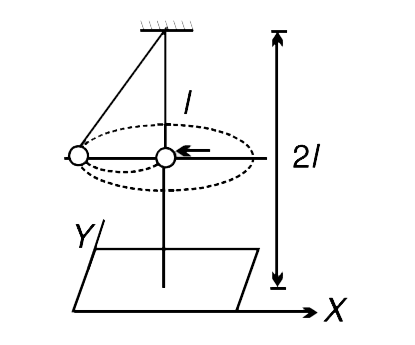
(a) Find tension in string just before the second collision.
(b) Find the height of the circular path above the floor.
(c) Find the time period of the circular motion.
(d) The string breaks during the circular motion at time t=0. At what time the bob will hit the floor ?
The correct Answer is:D
In perfectly inelastic collision with the horizontal surface the component parallel to the surface will remain unchanged. Similarly when the string becomes taut again, the component perpendicular to its length will remain unchanged.

cosθ=HLimpliesvc=√2gH
v2cosθ=(√2gH)H2L2=v (say)
∴h=v22g=(2gH)H4L42g=H5L4
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Comprehension Based Questions
3 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)
Displacement of the rod by the time the insect meet the moth is
View SolutionComprehension # 1
If net force on a system in a particular direction is zero (say in horizontal direction), we can apply: ΣmRxR=ΣmLxL,ΣmRvR=ΣmLvL and ΣmRaR=ΣmLaL
Here R stands for the masses which are moving towards right and L for the masses towards left, x is displacement, v is velocity and a the acceleration (all with respect to ground).
A small block of mass m=1kg is placed over a wedge of mass M=4kg as shown in figure. Mass m is released from rest. All surface are smooth. Origin O is as shown.

Final velocity of the wedge is ..........m/s :-
View SolutionIn the given figure, a=15m/s2 represents the total acceleration of a particle moving in the clockwise dirction in a circle of radius R=2.5m at a given instant of time. The speed of the particle is
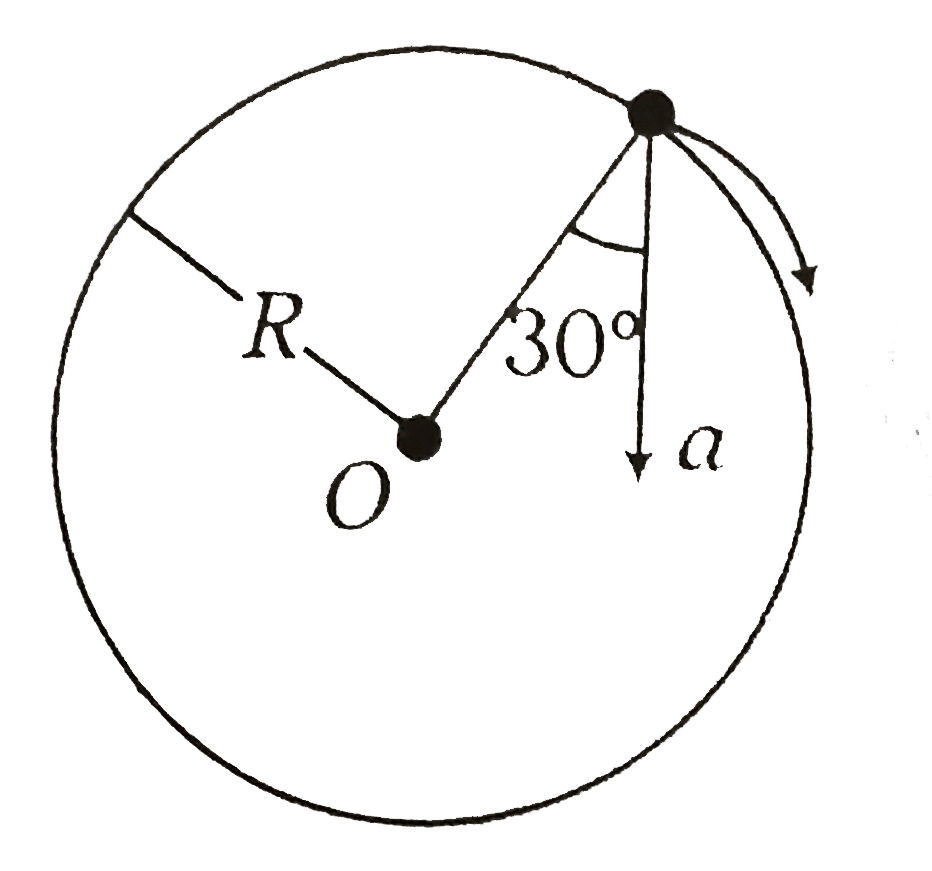
View SolutionA particle of mass 1kg is attached to a string of length 5m. The string is attached to a fixed point O. It is released from the position as shown in Fig. Calculate
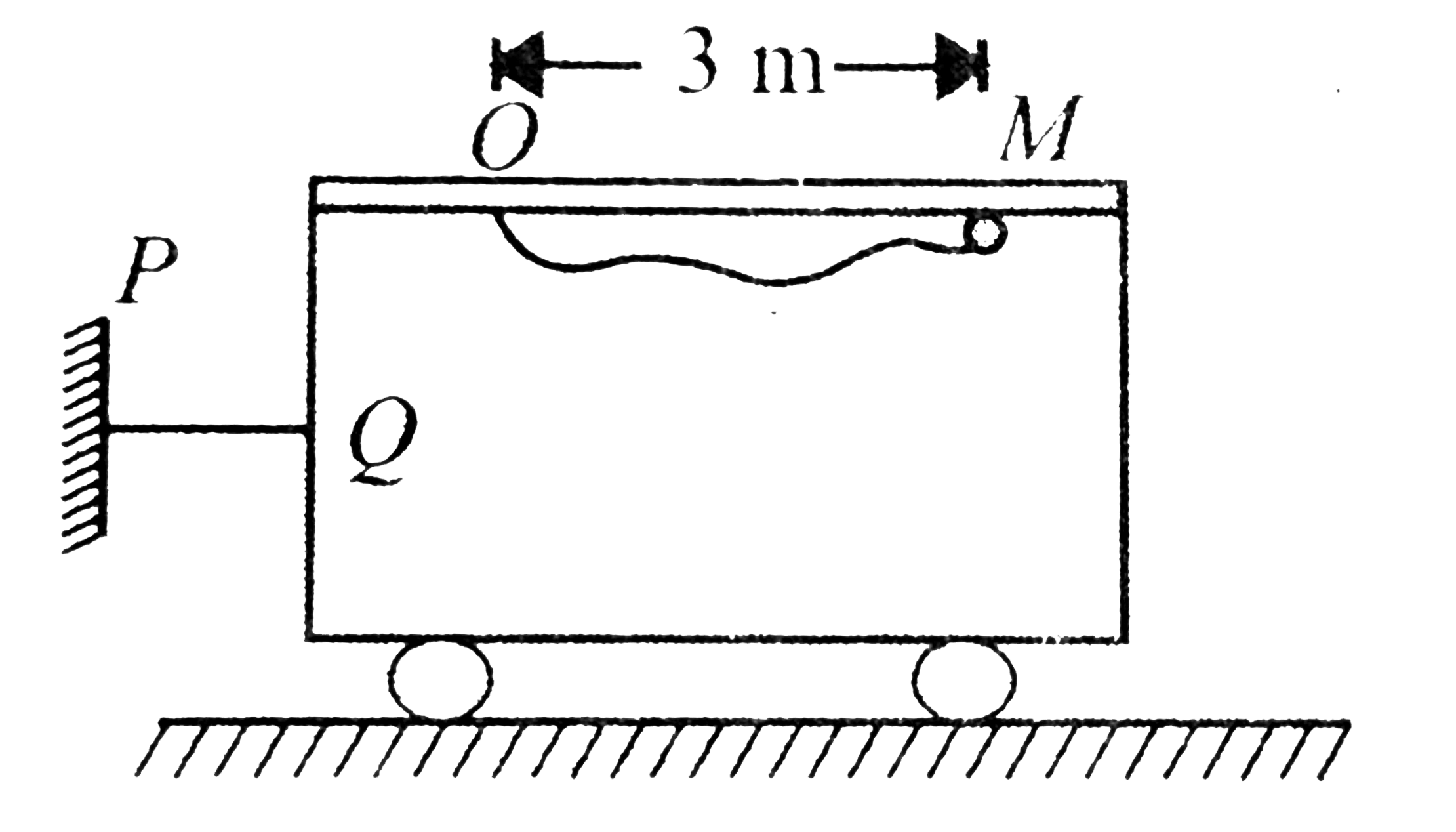
a. the impulse developed in the string when it becomes taut,
b. the velocity of the particle just after the string becomes taut,
c. the impulse developed in this string PQ at this instant.
View SolutionA heavy particle is attached to one end of a light string of length l whose other end is fixed at O. The oarticle is projectyed horizontally with a velocity v_0 from its lowest position A. When the angular displacement of the string is more than 90^(@) , the particle leaves the circular path at B. The string again becomes taut at C such that B,O,C are collinear. Find v_0 in terms of l and g
View Solution(i) O is a fixed peg at a height H above a perfectly inelastic smooth horizontal plane. A light inextensible string of length L(>H) has one end attached to O and the other end is attached to a heavy particle. The particle is held at the level of O with string horizontal and just taut and released from rest. Find the height of the particle above the plane when it comes to rest for the first time after the release.

(ii) The bob of a pendulum has mass m and the length of pendulum is l. It is initially at rest with the string vertical and the point of suspension at a height 2l above the floor. A particle P of mass m2 moving horizontally along –ve x-direction with velocity √2gl collides with the bob and comes to rest. The bob swings and when it comes to rest for the first time, another particle Q of mass m moving horizontally along y direction collides with the bob and sticks to it. It is observed that the bob now moves in a horizontal circle.

(a) Find tension in string just before the second collision.
(b) Find the height of the circular path above the floor.
(c) Find the time period of the circular motion.
(d) The string breaks during the circular motion at time t=0. At what time the bob will hit the floor ?
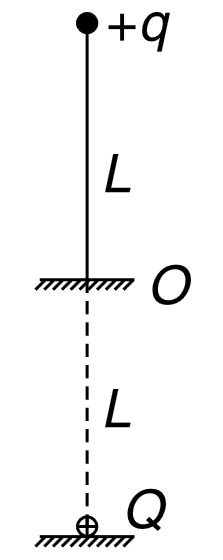
View SolutionA particle of mass m and charge q is attached to a light insulating thread of length L. The other end of the thread is secured at point O. Exactly below point O, there is a small ball having charge Q fixed on an insulating horizontal surface. The particle remains in equilibrium vertically above the ball with the string taut. Distance of the ball from point O is L. Find the minimum value of Q for which the particle will be in a stable equilibrium for any gentle horizontal push given to it.
View SolutionA heavy particle is attached to one end of a string 1m long whose other end is fixed at O. It is projected from it lowest position horizontally with a velocity V:
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u = sqrt((5)/(2)gl) The maximum angle made by the string with downward vertical is
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u = sqrt((5)/(2)gl) The tension in the string at an instant when acceleration of the particle is horizontal and sqrt(3)g is
View SolutionA mass is attached to the end of a string of length l which is tied to a fixed point O. The mass is released from the initial horizontal position of the string. Below the point O at what minimum distance a peg P should be fixed so that the mass turns about P and can describe a complete circle in the vertical plane?
View SolutionA heavy particle is tied to the end A of a string of the length 1.6 m. Its other end O is fixed. It revolves as a conical pendulum with the string making 60^(@) with the horizontal. Then,
View SolutionA particle of mass m is attached to one end of a string of length l while the other end is fixed to a point h above the horizontal table. The particle is made to revolve in a circle on the table so as to make p revolutions per second. The maximum value of p if the particle is to be in contact with the table will be :
View SolutionA particle of mass m is connected with a string of length 2 meter. Other end of the string is fixed with a point O at a height 1 m above the ground. The particle is thrown from some point in such a way that it strikes the ground (perfectly inelastic) with velocity v_(0) at an angle 37^(@) with vertical just below O.
View SolutionA particle of mass 'm' is attached to one end of a string of length 'l' while the other end is fixed to a point 'h' above the horizontal table, the particle is made to revolve in a circle on the table, so as to make P revolution per sec. The maximum value of P if the particle is to be contact with the table is
View Solution
