A thin metal disc of radius r floats on water surface and bends the surface downwards along the perimeter making an angle θ with vertical edge of the disc of the disc. If the disc dispplaces a weight of water W and surface tension of water is T, then the weight of metal disc is
2πrT+W
2πrTcosθ−W
2πrTcosθ+W
W−2πrTcosθ
The correct Answer is:C
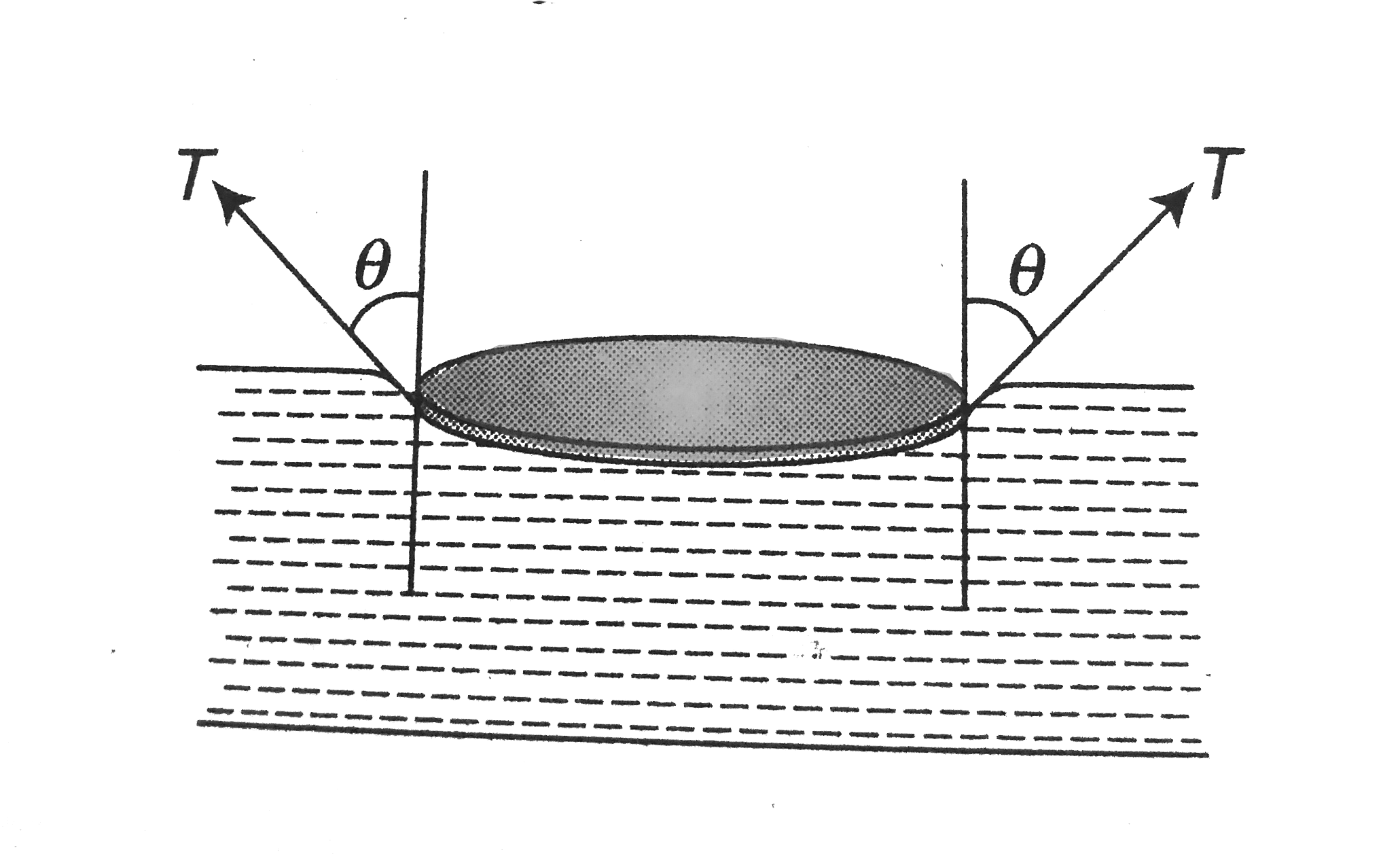
Weight of metal disc=total upward force
=upthrust force + force due to surface tension
=weight of displaced water +Tcosθ(2πr)
=W+2πrTcosθ
Topper's Solved these Questions
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Pressure Difference And Capillarity
Explore 23 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Viscosity
Explore 29 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Elasticity And Work Done In Stretching A Wire
Explore 25 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Chapter Test
Explore 29 Videos
Similar Questions
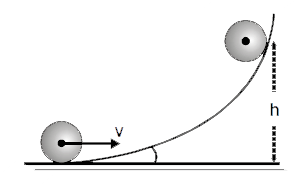
A disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be :-
View Solution
Knowledge Check
A thin metal disc of radius r floats on water surface and bends the surface downwards along the perimeter making an angle θ with vertical edge of the disc. If the disc displaces a weight of water W and surface tension of water is T, then the weight of metal disc is :
A2πrT+WB2πrTcosθ−WC2πrTcosθ+WDW−2πrTcosθA disc of paper of radius R is floating on the surface of water of surface tension T . If r=20 cm and T=0.070N//m , then the force of surface tension on the disc is
A2.2×10−2NB4.4×10−2NC8.8×10−2ND44×10−2NA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:
 A3v22gB3v24gCv24gDv22g
A3v22gB3v24gCv24gDv22g
A circular disc of radius r is rolling without slipping on a horizontal surface. What is the ratio of the translational KE and rotational KE of disc ?
View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density σ, rotates about its axis with an angular velocity ω. Find (a) the magnetic field induction at the centre of the disc (b) the magnetic moment of the disc.
View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density s rotates about its axis with an angular velocity ω. Find
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.
View SolutionA disc of radius R has a concentric hole of radius r. It is floating on a liquid of surface tension T . What is the force of surface tension on the disc ?
View SolutionA paper disc of radius R from which a hole of radius r is cut out is floating in a liquid of the surface tension S. The force on the disc due to the surface tension is
View Solution
