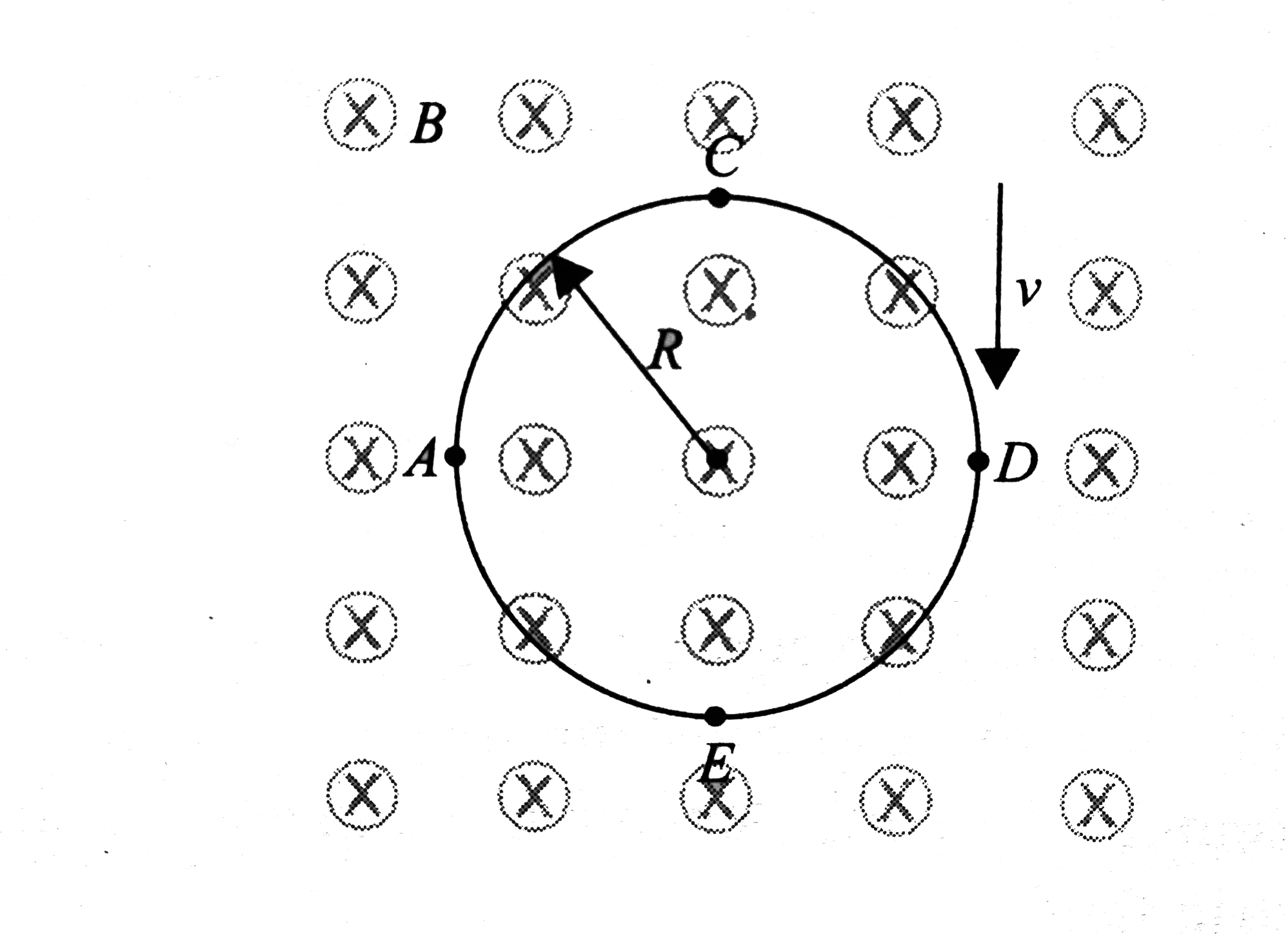
A thin semicircular conducting ring of radius R is falling with its plane vertical in a horizontal magnetic induction →B. At the position MNQ, the speed of the ring is v, the potential difference developed across the ring is:

Zero
12BvπR2 and M is the higher potential
πRBv and Q is at a higher potential
2RBv, and Q is at higher potential
Let semicircular ring falls through small distance dx from its position MNQ to M.Q.N.
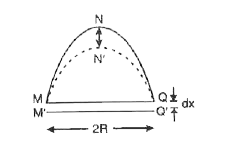
∴decrease in area of ring inside magnetic field
dA=−MQ.M.=−2Rdx
∴ change in Magnetic flux linked with ring
dϕB=B×dA=−2RBdx
∴ Potential difference developed across ring
E=−dϕBdt=2BRv
Topper's Solved these Questions
- E.M. INDUCTION AND A.C. CURRENTS BOOK - MODERN PUBLICATIONCHAPTER - E.M. INDUCTION AND A.C. CURRENTS EXERCISE - MULTIPLE CHOICE QUESTIONS LEVEL -III (QUESTIONS FROM AIEEE/JEE EXAMINATION)
14 Videos
- E.M. INDUCTION AND A.C. CURRENTS BOOK - MODERN PUBLICATIONCHAPTER - E.M. INDUCTION AND A.C. CURRENTS EXERCISE - RECENT COMPETITIVE QUESTIONS
31 Videos
- E.M. INDUCTION AND A.C. CURRENTS BOOK - MODERN PUBLICATIONCHAPTER - E.M. INDUCTION AND A.C. CURRENTS EXERCISE - RECENT COMPETITIVE QUESTIONS
31 Videos
- DESCRIPTION OF MOTION IN TWO AND THREE DIMENSIONBOOK - MODERN PUBLICATIONCHAPTER - DESCRIPTION OF MOTION IN TWO AND THREE DIMENSIONEXERCISE - Revision TEST
36 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - RECENT COMPETITIVE QUESTIONS
4 Videos
Similar Questions
A thin semi-circular conducting ring of radius R is falling with its plane verticle in horizontal magnetic induction (→B). At the position MNQ the speed of the ring is v, and the potential difference developed across the ring is
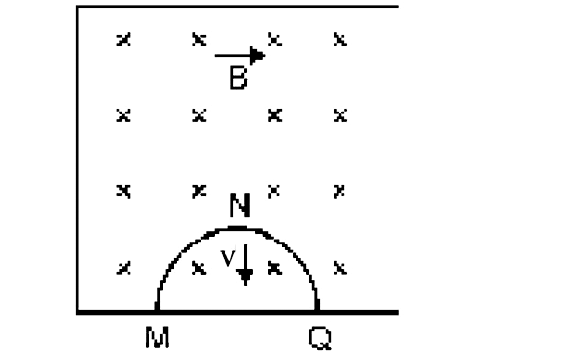
View SolutionA thin semicircular conducting ring of radius R is falling with its plane verticle in a horizontal magnetic inducting B. At the position MNQ, the speed of the ring is V and the potential difference developed across the ring is

(1.) zero
(2.)BcπR2/2
(3.) πRBV
(4.) 2RBV
View Solution
Knowledge Check
A thin semicircular conducting ring of radius R is falling with its plane vertical in a horizontal magnetic induction B. At the position MNQ, the speed of the ring is V and the potential difference developed across the ring is
 AZeroBBvπR2/2 and M is at higer potentialCπRBV and Q is at higer potentialD2RBV and Q is at higer potential
AZeroBBvπR2/2 and M is at higer potentialCπRBV and Q is at higer potentialD2RBV and Q is at higer potentialA thin semi-circular conducting ring of radius R is falling with its plane verticle in horizontal magnetic induction (→B). At the position MNQ the speed of the ring is v, and the potential difference developed across the ring is
 AzeroBBvπR2/2 and M is higher potencialCπ RBv ans Q is at higher potentialD2RBv ans Q is at higher potential
AzeroBBvπR2/2 and M is higher potencialCπ RBv ans Q is at higher potentialD2RBv ans Q is at higher potentialA thin circular -conducting ring having N turns of radius R is falling with its plane vertical in a horizontal magnetic field B . At the position MNQ the speed of ring is v the induced e.m.f developed across the ring is
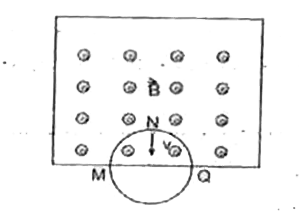 AZeroBBvπR2N2 and M is at higher potentialCNπ BRv and Q is at higher potentialD2RBvN and Q is at lower potential
AZeroBBvπR2N2 and M is at higher potentialCNπ BRv and Q is at higher potentialD2RBvN and Q is at lower potential
A thin semicircular conducting ring of radius R is falling with its plane vertical in a horizontal magnetic induction B. At the position MNQ shown in the fig, the speed of the ring is V. The potential difference developed across the semicircular ring is
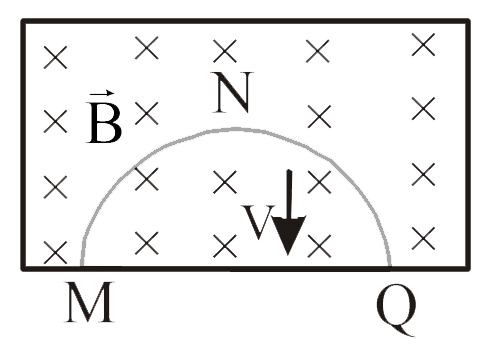
View SolutionA thin circular -conducting ring having N turns of radius R is falling with its plane vertical in a horizontal magnetic field B . At the position MNQ the speed of ring is v the induced e.m.f developed across the ring is

View SolutionA vertical conducting ring ogradius R falls vertically in a horizontal magnetic field of magnitude B. The direction of B is perpendicular to the plane of the ring. When the speed of the ring is v,
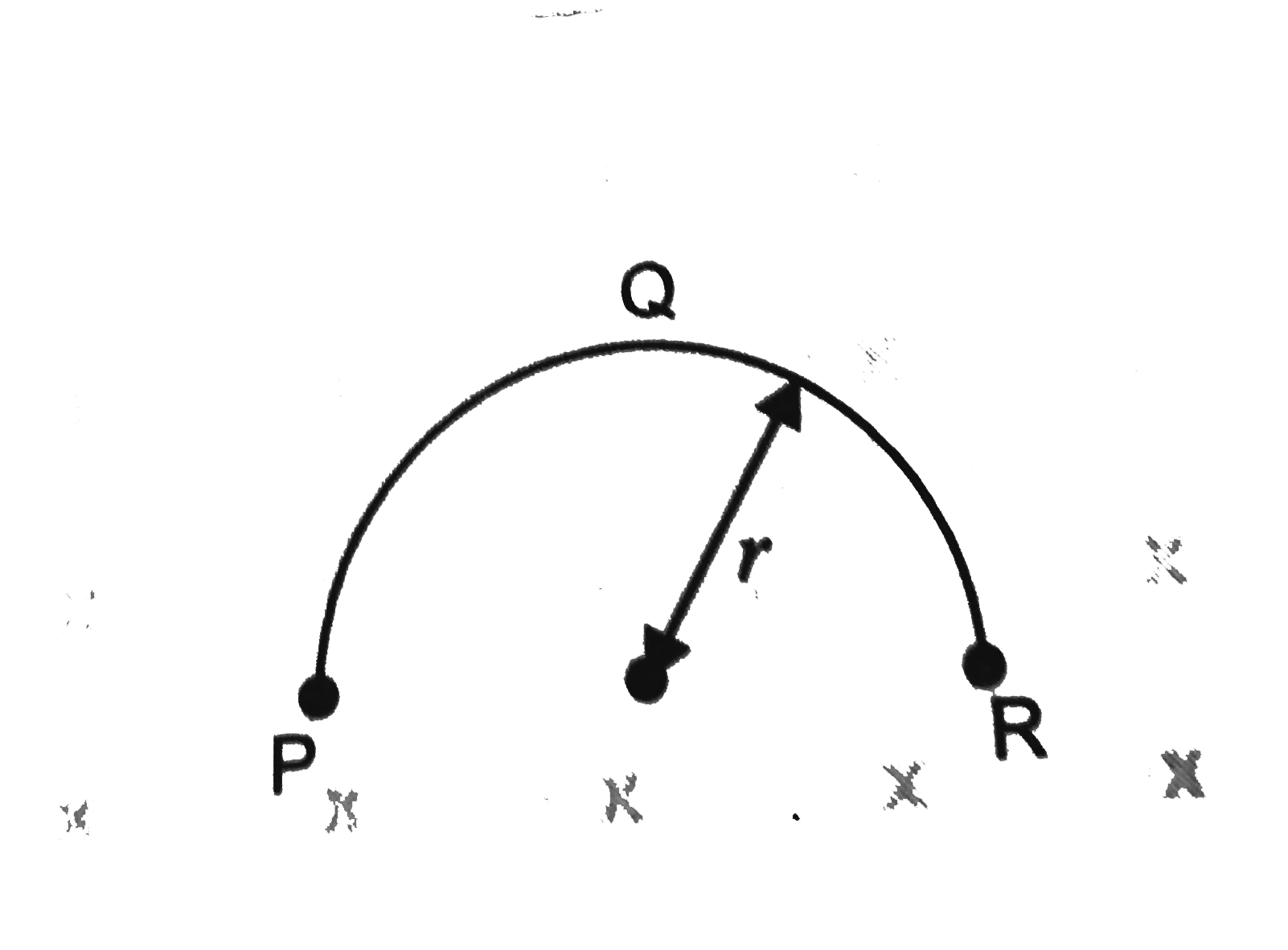
View SolutionA thin semicircuilar conducting ring (PQR) of radius r is falling with its plane vertical in a horizontal magnetic field B, as shown in Fig. The potential difference developed across the ring when its speed is υ, is
View SolutionA vertical conducting ring ogradius R falls vertically in a horizontal magnetic field of magnitude B. The direction of B is perpendicular to the plane of the ring. When the speed of the ring is v,

View Solution
