A thin uniform rod of length l and mass m is swinging freely about a h

A thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is $ω$ . Its cenre of mass rises to a maximum height of :
A $\frac{1 l ω}{6 g}$
B $\frac{1 l^{2} ω^{2}}{g}$
C $\frac{1 l^{2} ω^{2}}{6 g}$
D $1 \frac{l^{2} ω^{2}}{3 g}$
A uniform disc of mass $M$ and radius $R$ is pivoted about a horizontal axis passing through its edge. It is released from rest with its centre of mass at the same height as the pivot.

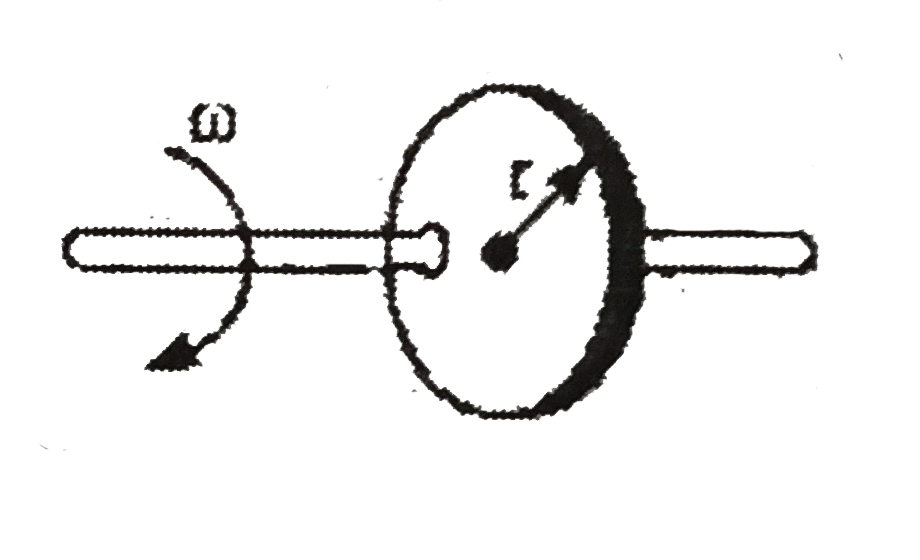AThe angular velocity of disc when its centre of mass is directly below the pivot is $\sqrt{\frac{4 g}{3 r}}$
BThe force exerted by the pivot at this instant is $\frac{7}{3} m g$
CAngular momentum of disc is conserved
DAngular acceleration of disc at the given instant is zero
The moment of inertia of a uniform rod of length $2 l$ and mass $m$ about an axis $x y$ passing through its centre and inclined at an angle $α$ is

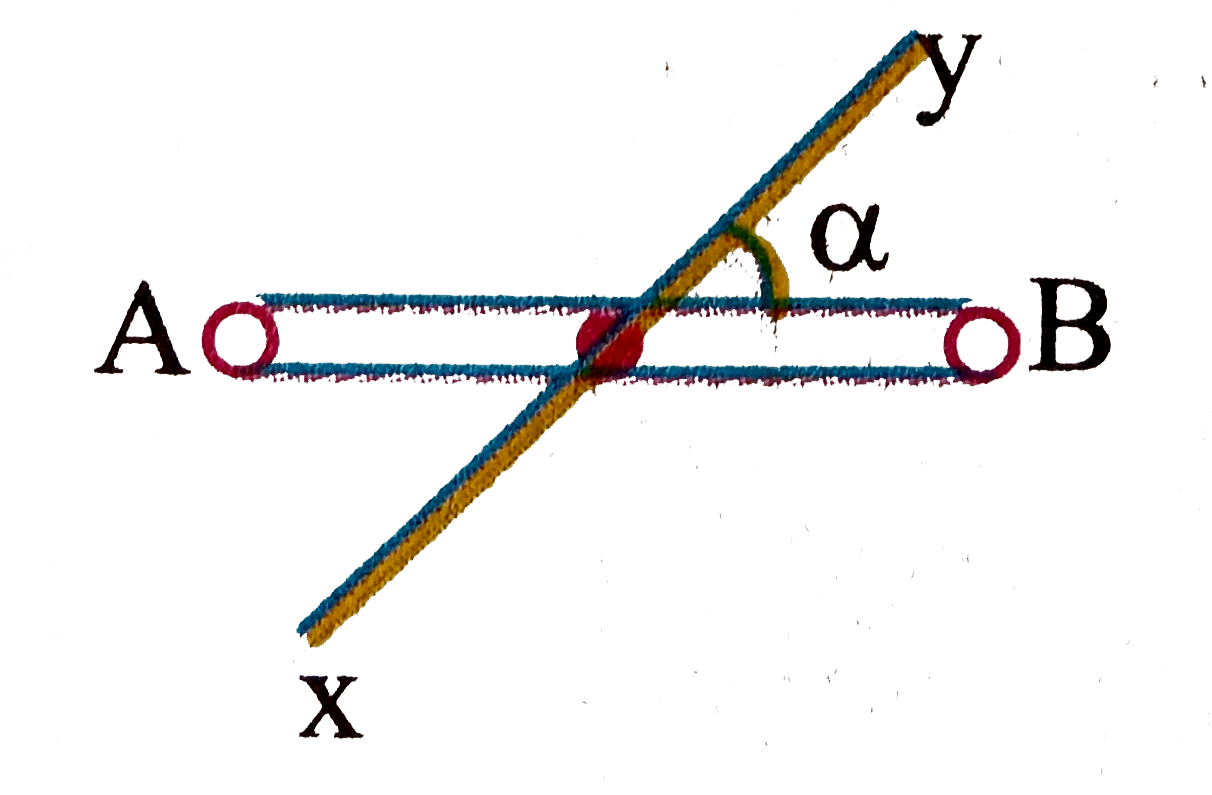A $\frac{m l^{2}}{3} {sin}^{2} α$
B $\frac{m l^{2}}{12} {sin}^{2} α$
C $\frac{m l^{2}}{2} {cos}^{2} α$
D $\frac{m l^{2}}{2} {cos}^{2} α$

A thin uniform rod of length $l$ and mass $m$ is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is $ω$ . Its centre of mass rises to a maximum height of -