Four particles, each of mass m, are lying symmetrically on the rim of a disc of mass M and radius R. M.I. of this system about an axis passing through one of the particles and perpendicular to plane of disc is
16mr2
(3M+19m)R22
(3M+12m)R22
zero
The correct Answer is:B
According to theorem of parallel axes, moment of inertia of disc about an axis passing through K and perpendicular to plane of disc =12MR2+MR2=32MR2
Total moment of inertia of the system
=32MR2+m(2R)2+m(2√R)2+m(√2R)2
=(3M+16m)R22
OD=R
∴ AC = 2R and AB= AD = R√2

Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ROTATIONAL MOTION'EXERCISE - MHT CET Corner35videos
ROTATIONAL MOTION'
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ROTATIONAL MOTION'EXERCISE - PRACTICE EXERCISE (Exercise 1 (TOPICAL PROBLEMS))70videos
ROTATIONAL MOTION'
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 225videos
REFRACTION OF LIGHT
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SCALARS AND VECTORS EXERCISE - Exercise 2 (Miscellaneous Problems)20videos
SCALARS AND VECTORS
Similar Questions
Calculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionFour similar point masses (each of mass m) are placed on the circumference of a disc of mass M and radius R. The M.I. of the system about the normal axis through the centre O will be:
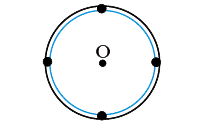 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Four particles each of mass m are lying symmetrically on the rim of a disc of mass M and radius R. Moment of inertia of this system about an axis passing through one of the particles and I to plane of disc is
A16mR2B(3M+16m)R22C(3m+12M)R22Dzero - Question 2 - Select One
Four similar point masses (m each) are symmetrically placed on the circumference of a disc of mass M and radius R. Moment of inertia of the system about an axis passing through centre O and perpendicular to the plane of the disc will be
AMR2+4mR2BMR2+85mR2CmR2+4MR2DMR22+4mR2 - Question 3 - Select One
The M.I. of disc of mass M and radius 'R' about an axis passing through midway between centre and circumference and perpendicular to its plane is
AMR2/2B5/4MR2CMR2D3/4MR2
Calculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionThe moment of Inertia of an incomplete disc of mas M and radius R as shown in figure about the axis passing through the centre and perpendicular to the plane of the disc is:
 View Solution
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point R2 away from the centre of disc, and perpendicular to the plane of disc is:
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point R2 away from the centre of disc, and perpendicular to the plane of disc is:
View Solution

