A thin, uniform rod with negligible mass and length 0.200m is attached to the floor by a frictionless hinge at point P (as shown in fig) A horizontal spring with force constant k=4.80Nm−1 connects the other end of the rod to a vertical wall. The rod to a vertical wall. The rod is in a uniform magnetic field B=0.340T directed into the plane of the figure. There is current I=6.50 A in the rod, in the direction shown.
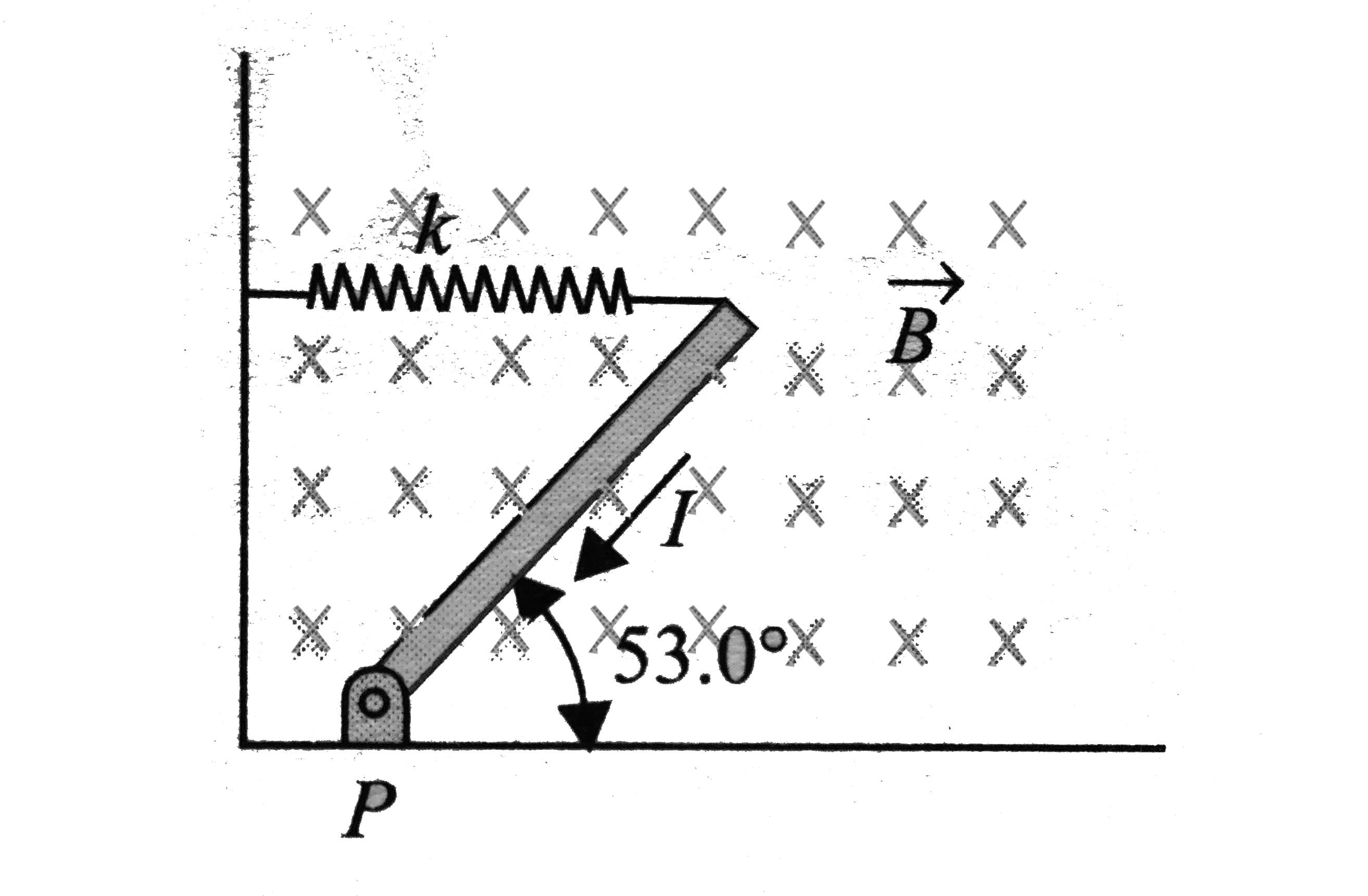
Calculate the torque due to the magnetic force on the rod, for an axis at P.
0.0442Nm−1, clockwise
0.0442Nm−1, anticlockwise
0.022Nm−1, clockwise
0.022Nm−1, anticlockwise
The correct Answer is:a
By exmining a small piece of the wire Fig. we find:

Dividing the rod into infinitiesimal sections of length dr.
The magnetic force on this section is dF1=IBdr and is
perpendicular to the rod. The torque dt due to forceon this section
is dtau=rdF1=IBrdr
The total torque is
∫dr=IB∫10rdr=12Il2B=0.0442Nm−1,
clockwise. This is the same torque calculated from a force diagram
in which the total magnetic force F1=ILB acts at the centre of
the rod.
F1 produces a clockwise torque, so the spring force must produce
a couterclockwise torque. The spring force must be to left,
the spring is stretched:
axis at hinge, counterclockwise torque positive
(kx)lsin53∘−12Il2B=0
x=IlB2ksin53.0∘=(6.50A)(0.200m)(0.340T)2(4.80Nm−1)sin53.0∘
=0.05765m
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Integer
7 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives Fill In The Blank
6 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Assertion -reasoning
8 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A thin, uniform rod with negligible mass and length 0.200m is attached to the floor by a frictionless hinge at point P (as shown in fig) A horizontal spring with force constant k=4.80Nm−1 connects the other end of the rod to a vertical wall. The rod to a vertical wall. The rod is in a uniform magnetic field B=0.340T directed into the plane of the figure. There is current I=6.50 A in the rod, in the direction shown.
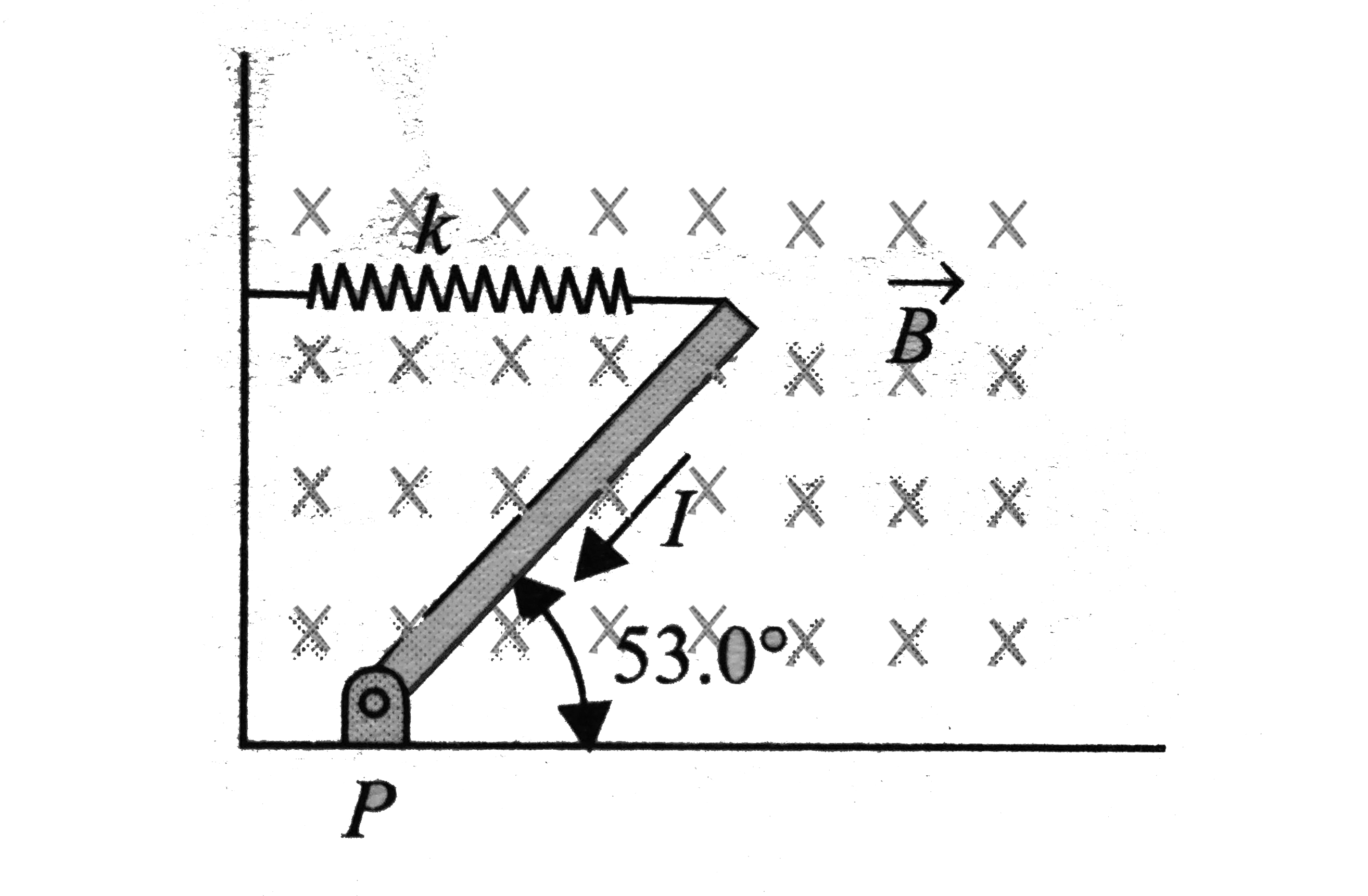
When the rod is in equilibrium and makes an angle of 53.0∘ with the floor, is the spring stretched or compressed?
View SolutionA thin, uniform rod with negligible mass and length 0.200m is attached to the floor by a frictionless hinge at point P (as shown in fig) A horizontal spring with force constant k=4.80Nm−1 connects the other end of the rod to a vertical wall.The rod is in a uniform magnetic field B=0.340T directed into the plane of the figure. There is current I=6.50 A in the rod, in the direction shown.

When the rod is in equilibrium and makes an angle of 53.0∘ with the floor, is the spring stretched or compressed?
View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is

View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in the figure. When string is cut, the initial angular accleration of the rod is.

View SolutionA conducting rod of length l is hinged at point O. It is a free to rotate in a verical plane. There exists a uniform magnetic field B in horizontal direction. The rod is released from the position shown. The potential difference between the two ends of the rod is proportional to
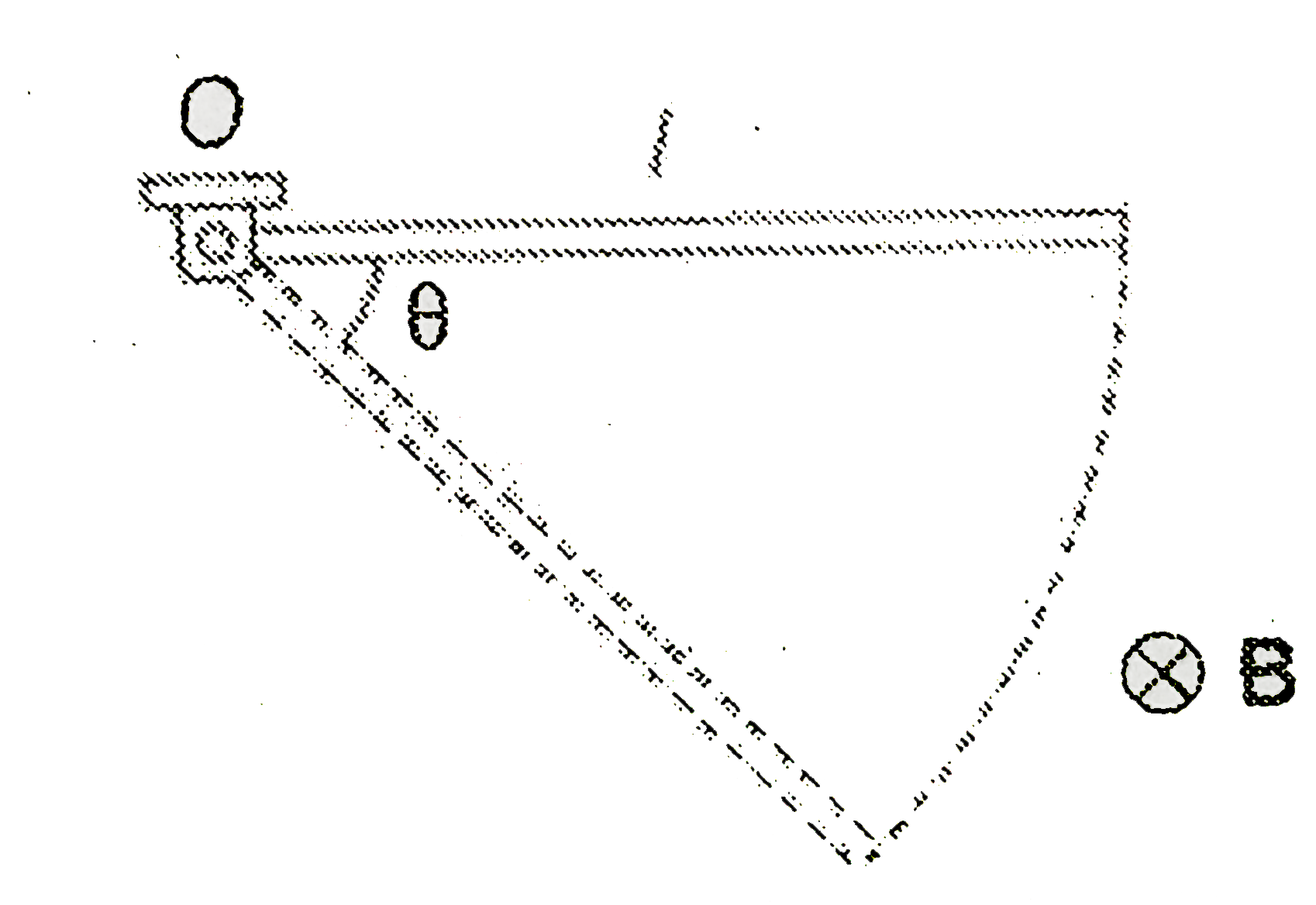
View Solution
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
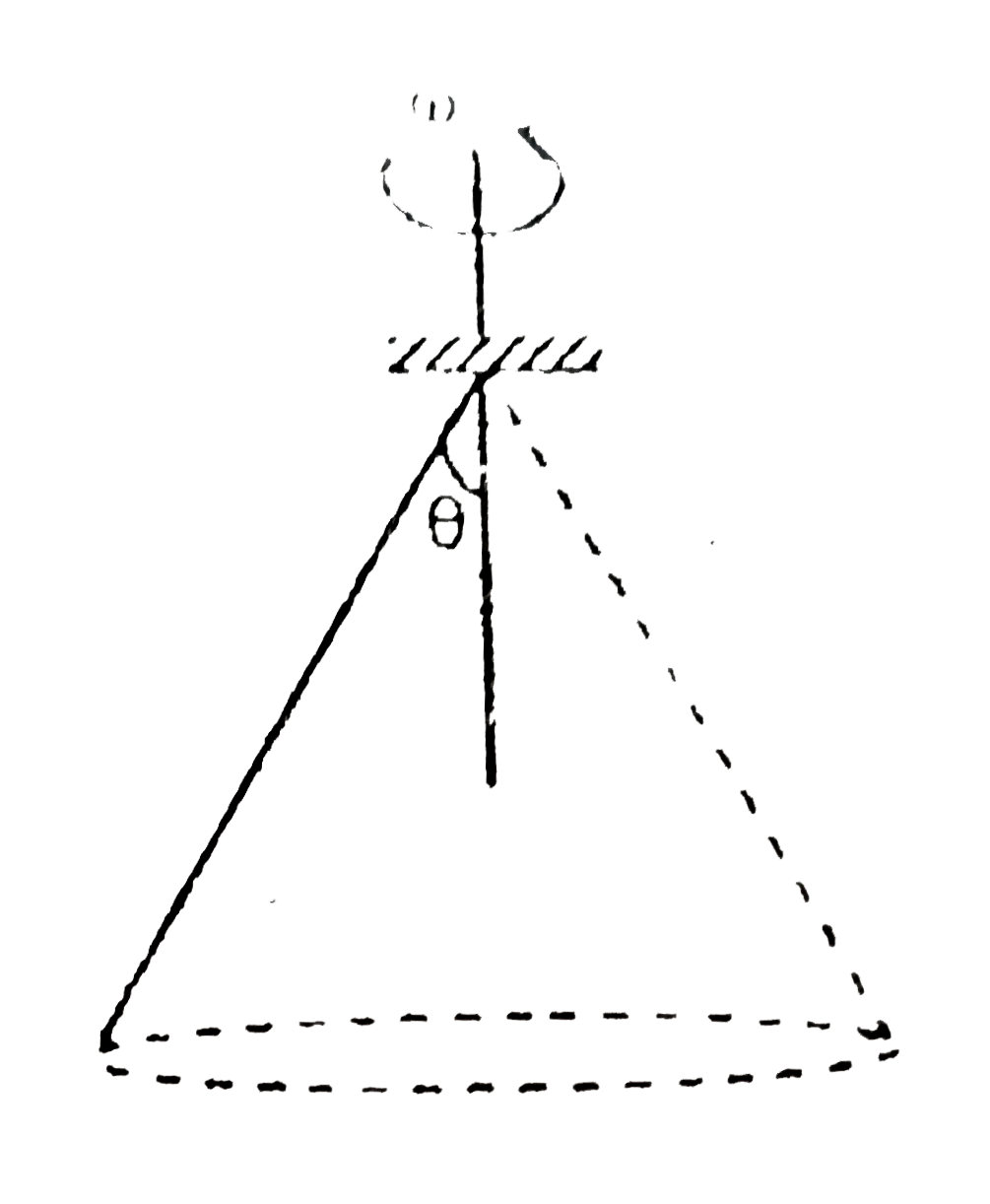
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
View SolutionA uniform rod of mass m and length L is kept on a horizontal table with L4 length on the table as shown in figure. As the string attached to the end B is cut, the angular acceleration of the rod about point C will be
_PHY_E05_242_Q01.png)
View SolutionA uniform rod of mass m length l is attached to smooth hinge at end A and to a string at end B as shown in figure. It is at rest. The angular acceleration of the rod just after the string is cut is :

View SolutionA massless rod rigidly fixed at O. A sting carrying a mass m at one end is attached to point A on the rod so that OA=a. At another point B(OB=b) of the rod, a horizontal spring of force constant k is attached as shown. Find the period of small vertical oscillations of mass m around its euqilibrium position.
_E01_116_Q01.png)
View Solution
